2.6. Сила давления на плоскую стенку. Гидравлический парадокс

Докажем, что полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление в центре тяжести этой площади, т.е. .

Пусть «абсолютно» покоящаяся жидкость ограничена плоской стенкой, наклоненной к горизонту под произвольным углом 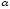(рис. 2.15).

Требуется определить силу давления жидкости на некоторый участок стенки, ограниченный произвольным контуром и имеющий площадь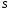. Чтобы увидеть форму этого участка, провести некоторые построения и найти положение центра тяжести его площади повернём стенку около её ребра на 90⁰, совместив её тем самым с площадью чертежа.

Рис. 2.15. Схема для определения силы давления жидкости

на плоскую стенку

Оси координат свяжем со стенкой и проведем их следующим образом: ось совместим с ребром стенки и направим вниз; осии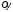расположим в плоскости, перпендикулярной к оси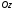; осьсовместим с линией пересечения свободной поверхности жидкости и стенки.

Выделим на рассматриваемом участке элементарную площадку и определим действующую на неё силу

,

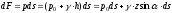где - давление на свободной поверхности;

- глубина расположения площадки ;

- координата площадки .

Для определения полной силы проинтегрируем полученное выражение по всей площади :

,

Последний интеграл представляет собой статический момент площади относительно осии равен произведению этой площади на координату ее центра тяжести (точка),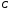

,

где - ордината центра тяжестиплощади.

Следовательно,

.

Учитывая, что глубина погружения центра тяжести , и выносяза скобки, получим

, (2.21)

где 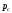- абсолютное давление в точке.

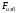В частном случае, когда давление является атмосферным и действует также с другой стороны стенки, то сила избыточного давления жидкости на плоскую стенку равна лишь силе давления от веса жидкости, т. е.

. (2.22)

Произведение представляет собой объем цилиндра с площадью основания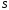, и высотой. Таким образом, физический смысл выражения (2.22):сила, с которой жидкость действует на плоскую стенку, равна весу жидкости в объеме цилиндра с основанием, равным площади данной стенки, и высотой, равной глубине погружения центра тяжести этой площадки под уровень свободной поверхности.

Формулу (2.22) можно ещё упростить

, (2.23)

где 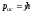- давление в центре тяжести площади.

Полученный результат может быть сформулирован так: сила давления жидкости на плоскую стенку равна произведению площади стенки на величину гидростатического давления в центре тяжести этой площади. Этот результат справедлив как для силы абсолютного, так и для силы избыточного давления.

Таким образом, сила давления покоящейся жидкости на плоскую стенку не зависит ни от формы стенки, ни от её наклона, а определяется лишь удельным весом жидкости, площадью участка стенки и глубиной погружения центра тяжести этой площади.

Это заключение вошло в литературу под названием гидростатического парадокса. Применительно к плоскому дну сосуда гидростатический парадокс сводится к тому, что сила давления жидкости на дно не зависит от формы сосуда и его дна, а определяется лишь площадью дна, уровнем жидкости в сосуде и её удельным весом.