7. Пуассоновский импульсный процесс

Р/м импульсный процесс вида

являющийся функцией случайных величин _i,  _i и  и сделаем ряд предположений:

1)Предположим, что функция F(t) затухает достаточно быстро, то есть

2)Будем считать, что величины _i и _i статистически независимы между собой и их распределения не зависят от номера i. Фактически это означает, что 2-мерная функция распределения этих величин распадается на множители:

3)Пусть вероятность появления импульса в интервале [t, t + dt] не зависит от времени t и количества предшествующих импульсов и пропорциональна длине интервала dt:

dP = dt,  = const.

Заметим, что последнее предположение в принципе может быть справедливо только на малых интервалах dt, поскольку dP  1.

Вычислим вероятность появления n импульсов на временном интервале [0, t] P(n, t). Эту вероятность можно представить как сумму вероятностей двух несовместных событий:

1)появление n импульсов на интервале [0, t – dt] и ни одного на интервале [t – dt, t];

2)появление n – 1 импульса на интервале [0, t – dt] и одного на интервале [t – dt, t].

Остальными вариантами можно пренебречь и малость интервала [t – dt, t]. Таким образом

P(n, t) = P(n, t – dt)(1 – dt) + P(n – 1, t – dt)dt.

Полагая

при dt  0 получим:

или

Введем производящую функцию вида

и преобразуем полученное выражение, домножив его на sⁿ и суммируя по всем n:

Учитывая, что

получим уравнение для производящей функции:

Решение этого уравнения имеет вид

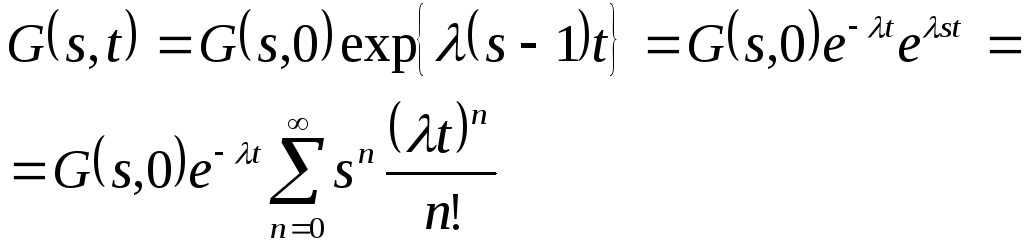
Поскольку P(0, 0) = 1 и P(n  1, 0) = 0, получаем

G(s, 0) = 1, поэтому

Таким образом, мы показали, что распределение вероятностей совпадает с распределением Пуассона

(2.6)

причем величина t = <n>. Это означает, что среднее число импульсов, появившихся на интервале [0, t] пропорционально длительности этого интервала. Поскольку вероятность того, что на интервале [0, t] не появилось ни одного импульса, равна P(0, t) = e^–t, вероятность того, что интервал между двумя соседними импульсами  лежит в диапазоне [t, t + dt] можно найти как произведение вероятностей двух независимых событий – того, что за время t ни одного импульса не появилось и того, что на интервале [t, t + dt] появился один импульс:

Поскольку по определению P{t    t + dt} = (t)dt, легко записать вид функции плотности вероятности:

Теперь можно вычислить средний интервал между импульсами:

Параметр распределения  имеет смысл средней частоты следования импульсов.

Выберем интервал наблюдения 0  t  T много большим как величины 1/, так и длительности одного импульса (то есть F(T) = 0). Тогда импульсы, появившиеся за пределами данного интервала, не будут вносить значительный вклад в функцию (t) и можно пренебречь краевыми эффектами, то есть влиянием тех импульсов, которые попадают в интервал частично. Найдем распределение (x) случайной величины (t), то есть вероятность события A, заключающегося в том, что x  (t)  x + dx

Очевидно, событие A (рис. 2.2) может реализоваться в результате появления за интервал наблюдения любого количества импульсов, поэтому используя формулу полной вероятности, мы можем записать

Рис. 2.2. Распределение случайной величины (t)

Здесь (x|n) – условная функция плотности вероятности величины (t) при условии, что за время T появилось n импульсов. Т.е. моменты случайной величины (t) равны

где m_k(|n) – условные моменты величины (t) при условии появления n импульсов за интервал [0, T]. Вычислим первый условный момент, основываясь на определении (t) и на предположении 2 о независимости случайных амплитуд _i и моментов появления _i:

Здесь

среднее значение _i, не зависящее от i.

Теперь р/м среднее <F(t – t_i)>; для его определения необходимо задать функцию плотности вероятности _(t_i). Будем считать, что момент появления i-го импульса распределен равномерно на интервале [0, T], то есть _(t_i) = 1/T. Тогда

Здесь мы воспользовались локализованностью функции F(t). Подставляя полученное выражение (2.9) в формулу (2.8), запишем

Учитывая, что входящая в это выражение вероятность P(n) определяется распределением Пуассона (2.6) при t = T, то есть P(n) = P(n, T), получим

Совершенно аналогично найдем второй условный момент

Поскольку согласно нашим предположениям величины _i и _I независимы, получим:

Таким образом, второй условный момент равен

Подставляя это выражение в формулу (2.8) с k = 2, получим

Учитывая, что для распределения Пуассона

<n²> = <n>² + <n>, применяя соотношение (2.10), а также учитывая, что средняя частота следования импульсов  = <n>/T, запишем

Таким образом, дисперсия процесса определяется выражением

В частном случае, если импульсы имеют одинаковую высоту, то есть _i = a, на основе (2.10) и (2.11) получаем

Эта пара соотношений называется теоремой Кэмпбелла.