
- •Дать определение частоты появления события и сформулировать аксиому измерений.
- •Записать формулу полной вероятности и формулу Байеса.
- •Сформулировать закон больших чисел и теорему Бернулли.
- •Сформулировать условия, при которых распределение пуассоновского импульсного процесса близко к нормальному.
- •Сформулировать теорему Кемпбелла для пуассоновского импульсного процесса.
- •Дать определения непрерывности, дифференцируемости, интегрируемости и стационарности случайной функции.
- •Дать определение белого шума и привести его функцию автокорреляции и спектральную плотность интенсивности.
- •Записать спектральную плотность интенсивности процесса на выходе линейной системы, на вход которой воздействует случайный процесс.
- •Сформулировать теорему о нормализации.
- •Записать уравнение фпк, пояснить смысл его коэффициентов и привести условия, при котором оно существует.
Экзаменационная программа курса
«Статистическая радиофизика»
Минимальные требования
ОТВЕТЫ НА МИНИМУМ!
-
Дать определение частоты появления события и сформулировать аксиому измерений.
Если в серии из N экспериментов, выполняющихся при определенном комплексе условий, событие A произошло n раз, то = n/N – частота появления события A в N экспериментах. Ясно, что тот факт, что при N экспериментах n раз произойдет событие A, также является случайным событием, а частота появления – случайной величиной.
Предположение, что
![]() называется аксиомой измерения.
Ясно, что 0 P{A}
1.
называется аксиомой измерения.
Ясно, что 0 P{A}
1.
-
Записать формулу полной вероятности и формулу Байеса.
Если есть K взаимно независимых событий A1 … AK, причем вероятность P{A1 + A2 + … + AK} = 1, то есть одно из них непременно произойдет, то говорят, что имеется полная группа из K гипотез, тогда для абсолютно любого события В
 -
формула полной вероятности.
-
формула полной вероятности.
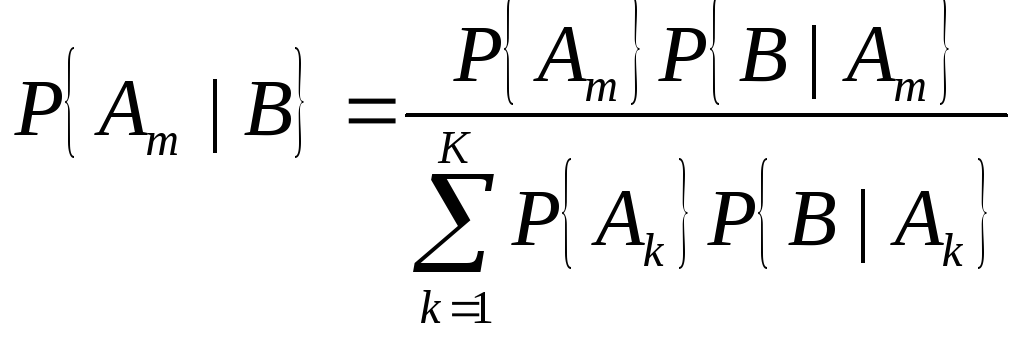 -
формулу Байеса.
-
формулу Байеса.
-
Сформулировать закон больших чисел и теорему Бернулли.
Рассмотрим случайный процесс
![]() (где
(где
![]() - попарно независимы). Для всякого
- попарно независимы). Для всякого
> 0 выполняется равенство
![]() ,
которое называется законом больших
чисел или теоремой Чебышева.
,
которое называется законом больших
чисел или теоремой Чебышева.
Говорят, что если для всякого
> 0 справедливо
![]() ,
то последовательность N
сходится к числу a по
вероятности. Сходимость по вероятности
обозначается следующим образом:
,
то последовательность N
сходится к числу a по
вероятности. Сходимость по вероятности
обозначается следующим образом:
![]() .
.
Согласно теореме Чебышева
![]()
т.е.
![]() -
теорема Бернулли: частота
появления события A
сходится по вероятности к величине p
– вероятности события A
в математическом смысле,
-
теорема Бернулли: частота
появления события A
сходится по вероятности к величине p
– вероятности события A
в математическом смысле,
![]() -
другая запись теоремы Бернулли; то есть
среднее арифметическое сходится по
вероятности к математическому ожиданию.
-
другая запись теоремы Бернулли; то есть
среднее арифметическое сходится по
вероятности к математическому ожиданию.
-
Записать формулы для распределений Гаусса, Релея и Пуассона.
![]() -
нормальное распределение
(распределение Гаусса), для
которого
-
нормальное распределение
(распределение Гаусса), для
которого
![]() ,
,
![]() .
.
![]() -
распределение Пуассона.
-
распределение Пуассона.
![]() -
распределением Рэлея.
-
распределением Рэлея.
-
Дать определение характеристической функции и записать выражения, связывающие ее с функцией плотности вероятности.
По определению характеристической функцией называется среднее от комплексной экспоненты
<exp(ju)>
=
![]() ,
где
,
где
![]()
-
Сформулировать центральную предельную теорему.
Пусть 1,…, N – набор независимых случайных величин, средние значения которых равны соответственно <i> = ai, дисперсии ограничены и равны M2(i) = i2 < C < . Если для любого > 0 выполняется равенство
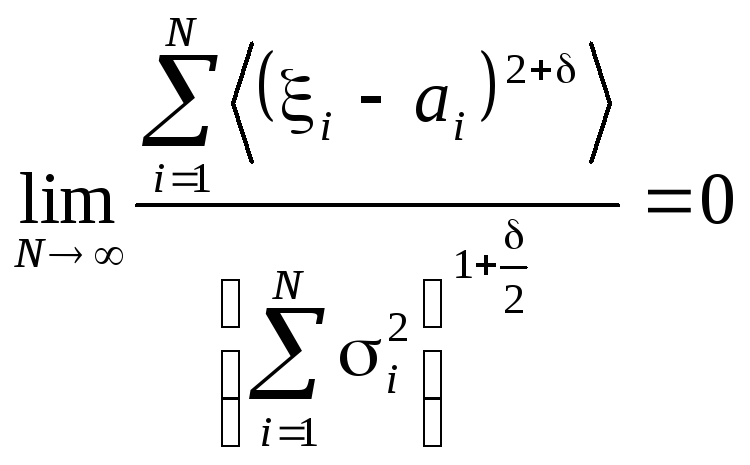 ,
,
то случайная величина
![]() имеет распределение, равномерно
сходящееся к нормальному при N
независимо от распределения слагаемых.
имеет распределение, равномерно
сходящееся к нормальному при N
независимо от распределения слагаемых.
-
Записать выражение для плотности вероятности одномерной функции случайной величины.
Пусть существует функция x=g(y), обратная бесконечно дифференцируемой функции y=f(x), тогда функция плотности вероятности одной случайной величины через другую:
![]()
-
Привести вид пуассоновского импульсного процесса, сформулировать предположения, при которых он рассматривается и записать выражение для вероятности появления n импульсов на интервале [0, t].
Рассмотрим импульсный процесс вида:
![]()
являющийся функцией случайных величин i, i и и сделаем ряд предположений:
-
Предположим, что функция F(t) затухает достаточно быстро, то есть
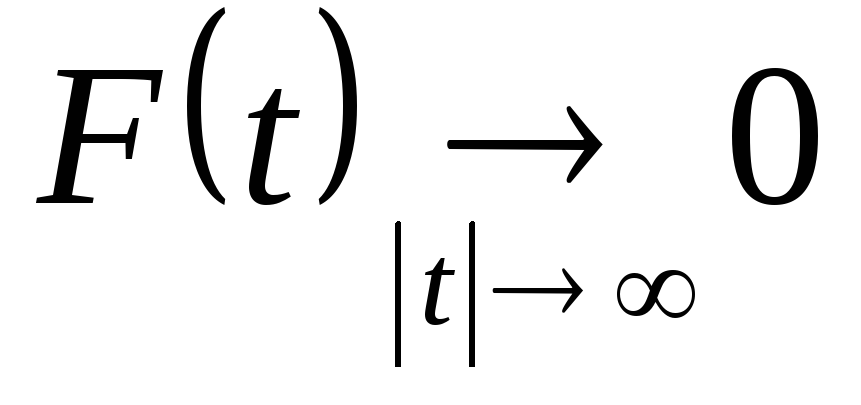 .
. -
Будем считать, что величины i и i статистически независимы между собой и их распределения не зависят от номера i. Фактически это означает, что 2-мерная функция распределения этих величин распадается на множители:
![]() .
.
-
Пусть вероятность появления импульса в интервале [t, t + dt] не зависит от времени t и количества предшествующих импульсов и пропорциональна длине интервала dt: dP = dt, = const.
![]()
Здесь (x|n) – условная функция плотности вероятности величины (t) при условии, что за время T появилось n импульсов.
