
- •1.Случайные величины.Распределение вероятностей.Аксиома измерений.
- •2. Закон больших чисел. Теорема Бернулли
- •7. Пуассоновский импульсный процесс
- •8.Случайные функции: их задание, сходимость, непрерывность и стационарность.
- •9. Моменты случайных функций
- •10. Эргодические случайные процессы
- •11. Функция автокорреляции
- •12. Спектральные характеристики случайных процессов
- •13. Корреляционная теория случайных последовательностей
- •14. Спектр процесса на выходе линейной системы
- •15. Распределение вероятностей на выходе линейной системы. Теорема о нормализации
- •16. Узкополосный гауссов процесс
- •17. Спектр колебаний с флуктуирующей частотой
- •19. Нелинейное безинерциальное преобразование. Корреляц-ые фии на выходе генератора гармоник
- •20. Марковские процессы .Уравнение Смолуховского
- •21. Марковский процесс с дискретными состояниями
- •22. Двумерные случайные блуждания
- •23. Уравнение Фоккера-Планка-Колмогорова
- •24. Стохастические дифференциальные уравнения. Случайные функции с независимыми приращениями
- •25. Усреднение точного решения стохастического дифференциального уравнения
- •26. Уравнение для средних и его связь с уравнением фпк.
- •27. Уравнение Лиувилля.Случайный телеграфный сигнал.
- •28. Тепловой шум в линейных диссипативных системах. Теорема Найквиста
- •29. Дробовой и фликкер-шум. Шумы полупроводниковых приборов
- •30. Шумы усилителей
- •31. Корреляционные и спектральные характеристики случайного поля
- •32. Эмв в статистически неоднородной среде
- •33. Анализ случайной дифракции методом мма
- •34. Плоская случайная волна в диспергирующей среде
- •35. Корреляционная функция одномодового и многомодового лазерного излучения
1.Случайные величины.Распределение вероятностей.Аксиома измерений.
Предметом теории вероятностей являются массовые явления – длинные серии экспериментов при определенном комплексе условий. Если при воспроизведении данного комплекса условий результаты экспериментов также воспроизводятся, процесс называют детерминированным. В противном случае процесс является случайным.
Каждому результату эксперимента можно поставить в соответствие некоторую величину или событие. Если в серии из N экспериментов, выполняющихся при определенном комплексе условий, событие A произошло n раз, то = n/N – частота появления события A в N экспериментах. Ясно, что тот факт, что при N экспериментах n раз произойдет событие A, также является случайным событием, а частота появления – СВ. Введем вероятность случайного события A как величину, мало отличающуюся от при больших N. Предположение
|
|
(1.1) |
Ясно, что 0 P{A} 1. Для двух взаимосвязанных событий можно ввести условную вероятность P{A|B}, то есть вероятность возникновения события A при условии, что произошло событие B. Из частотного определения вероятности следует, что
|
P{A|B} = P{AB}/P{B}, P{B|A} = P{AB}/P{A} |
(1.2) |
Отсюда
|
вероятности P{A} часто называют априорными |
(1.3) |
, а условные P{A|B} – апостериорными. Если события A и B независимы, то в соответствии с (1.2) P{A|B} = P{A}, P{B|A} = P{B}, то есть P{AB} = P{A}P{B}.Если есть K взаимно независимых событий A1 … AK, причем вероятность P{A1 + A2 + … + AK} = 1, то есть имеется полная группа из K гипотез, то
|
|
(1.4) |
формула полной вероятности.
|
|
(1.5) |
Р/м непрерывную или дискретную случайную величину как результат некоторого эксперимента и поставим ей в соответствие множество случайных событий, заключающихся в том, что = xi (для дискретной величины) или
x < < x + x (для непрерывной величины). Закон по которому каждому значению xi (или интервалу x) ставится в соответствие вероятность того, что примет это значение (попадет в этот интервал), называют законом распределения. Аналитическим выражением закона распределения является функция распределения. Введем интегральную функцию распределения как F(x) = P{ x},ее свойства: F(–) = 0, F() = 1,
F(x1) F(x2) если x1 x2.Производная интегральной ф-ии:
|
|
(1.6) |
называют функцией плотности вероятности.
![]()
![]() -ф-ия
плотноси вероятности для дискретной
сл. Величины.
-ф-ия
плотноси вероятности для дискретной
сл. Величины.
Среднее значение произвольной функции случайной величины f() как
![]() для
непрерывной величины и
для
непрерывной величины и
![]()
для дискретной. Для любой случайной величины можно ввести моменты n-го порядка, которые определяются как среднее от n. Для непрерывной и дискретной случайных величин момент n-го порядка равен соответственно
![]()
Среднее
или первый момент случайной величины
называется математическим
ожиданием:
![]()
Центральные моменты:
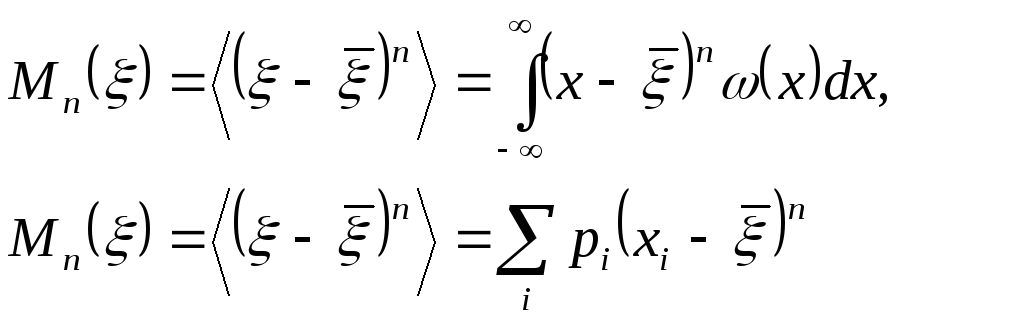
Центральный момент второго порядка называется дисперсией:
![]()
![]()
Р/м ряд примеров распределений случайных величин. Пусть эксперимент имеет только два исхода – либо происходит событие A с вероятностью P{A} = p, либо событие B с вероятностью P{B}= q = 1 – p. Тогда вероятность того, что при N испытаниях n раз произойдет событие A определяется биноминальным законом распределения:
![]() (**)
(**)
Моменты этого распределения:

Первый и второй моменты:
![]()
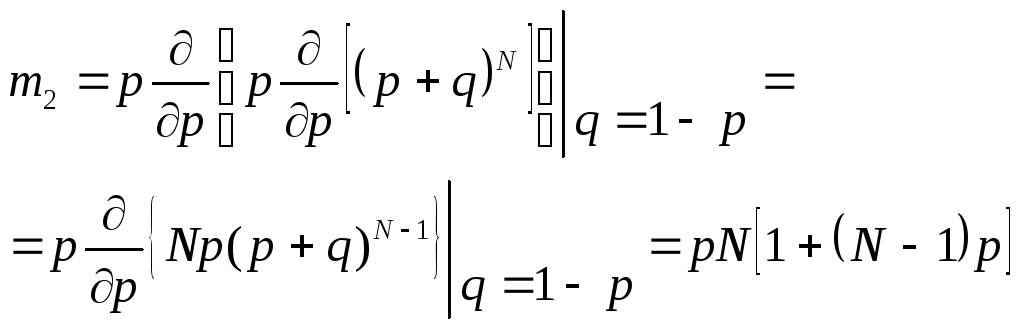
Дисперсия:
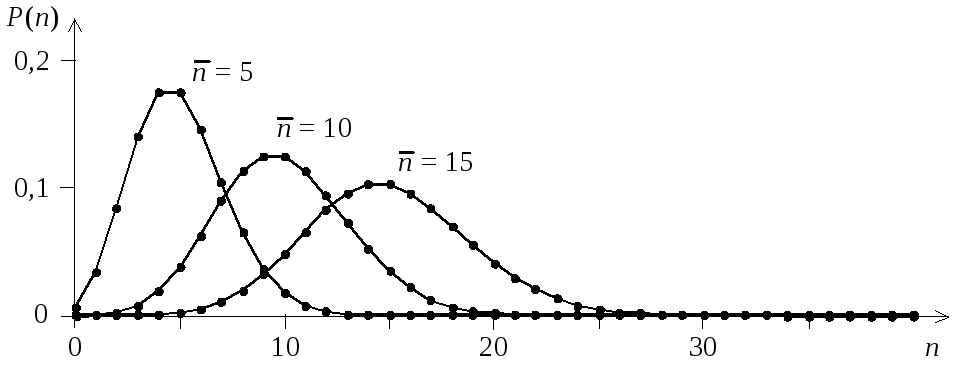
![]() Вид
биноминального закона распределения
(**) при p
= 0,1 и различных значениях N
показан на рис. 1.1.
Вид
биноминального закона распределения
(**) при p
= 0,1 и различных значениях N
показан на рис. 1.1.

Рис. 1.1. Биноминальный закон распределения
Будем
увеличивать число испытаний N
так, чтобы произведение Np
= m1
= <n>
оставалось постоянным (вероятность p
при этом будет уменьшаться). Сделаем
ряд преобразований выражения (**):
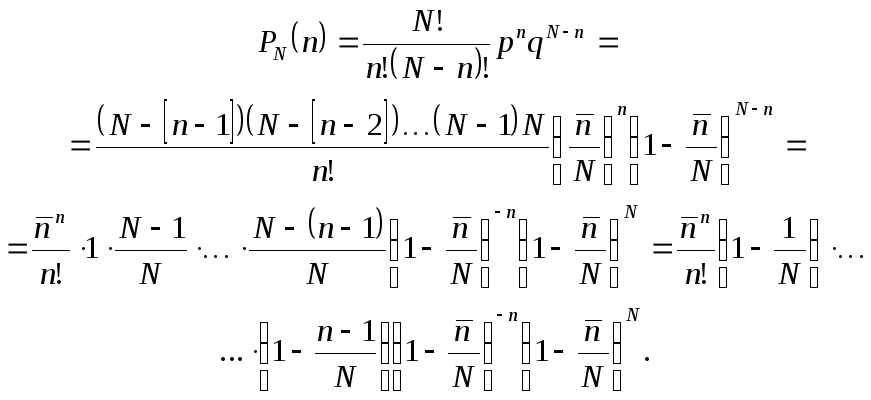
Известно:
![]()
получим
|
|
(1.10) |
распределение Пуассона (рис. 1.2).
 Вычисление
моментов этого распределения дает:
Вычисление
моментов этого распределения дает:
![]()
Формулы для первых двух моментов и дисперсии распределения Пуассона имеют вид:
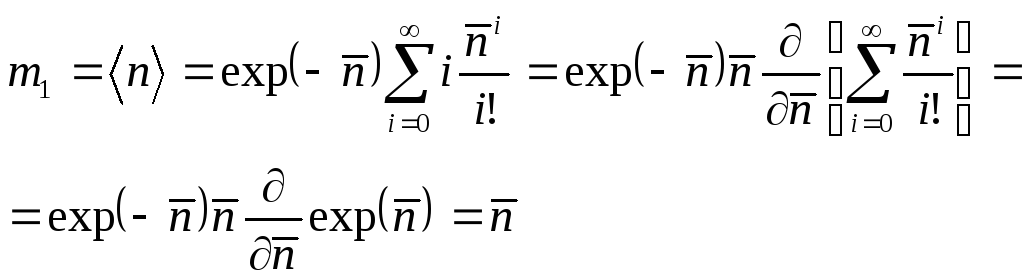
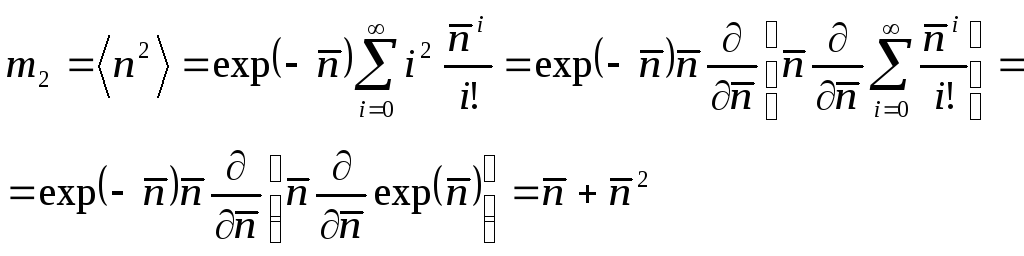
![]()

Рис. 1.3. Распределение Муавра-Лапласа
Устремим в (**) N к при постоянной вероятности p = const (p 0 и p 1). Получим
|
|
(1.11) |
распределение Муавра-Лапласа (рис. 1.3)
![]() Эта
функция описывает нормальное
распределение
(распределение
Гаусса),
Эта
функция описывает нормальное
распределение
(распределение
Гаусса),
![]()
![]() При
больших значениях n
можно пренебречь дискретностью и от n
перейти к непрерывной величине
с функцией плотности вероятности вида
При
больших значениях n
можно пренебречь дискретностью и от n
перейти к непрерывной величине
с функцией плотности вероятности вида
|
|
(1.12) |
Эта функция описывает нормальное распределение (распределение Гаусса), для которого
![]()
![]()
Вид распределения Гаусса показан на рис. 1.4.
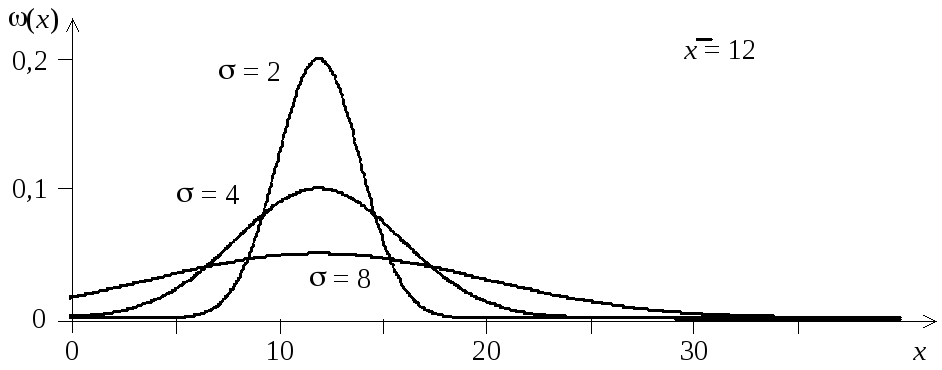
Рис. 1.4. Распределение Гаусса

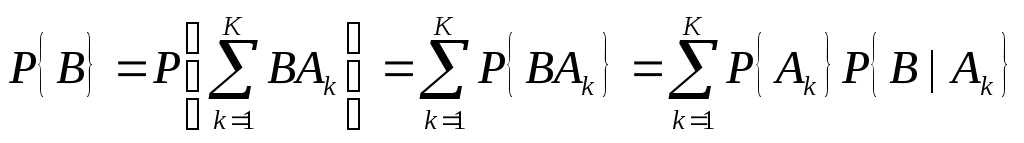
 формула
Байеса:
формула
Байеса: