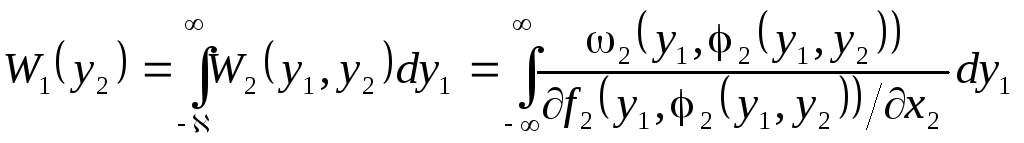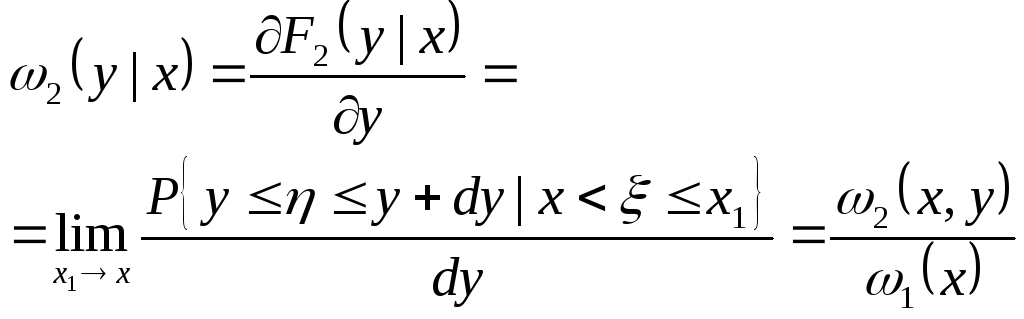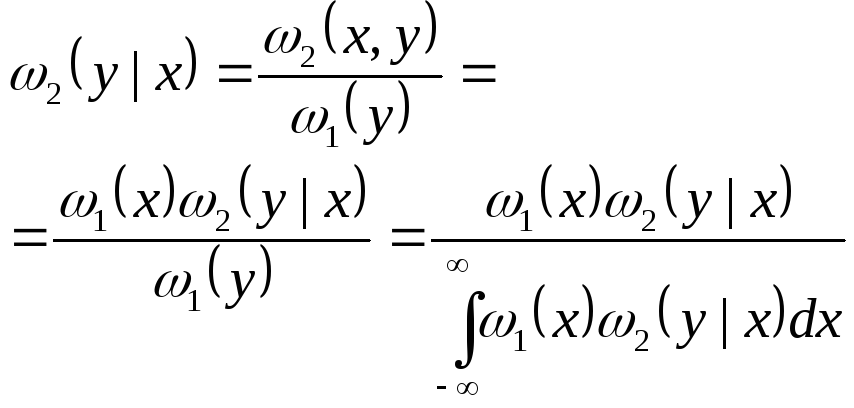2. Закон больших чисел. Теорема Бернулли

Р/м СВ , имеющую конечную дисперсию ² и среднее, равное . Для любого числа

Поскольку вне интервала

величина заведомо больше, получим:

Положив a = , получим

неравенство Чебышева.

(1.13)

Р/м теперь СВ _N, которая является средним арифметическим набора из N попарно независимых случайных величин _I

дисперсии этих величин конечны D()  C. Очевидно, дисперсия величины _N также будет ограничена:

Используя неравенство Чебышева, мы можем записать

Тогда

Таким образом, для всякого  > 0 выполняется равенство

(1.14)

закон больших чисел или теоремой Чебышева, для всякого  > 0

то последовательность _N сходится к числу a по вероятности. Сходимость по вероятности обозначается следующим образом:

Рассматривая серию из N испытаний, появлению некоторого события A в испытании с номером i поставим в соответствие _i = 1, в противном случае будем считать _i = 0. Тогда

частота появления события A. получим

Согласно теореме Чебышева (1.14), можно записать

или

(1.15)

Таким образом, частота появления события A сходится по вероятности к величине p –вероятности события A в математическом смысле. Доказанное утверждение носит название теоремы Бернулли Другими словами, частотное определение вероятности является вполне корректным способом установления соответствия между чисто математическим понятием (вероятностью p), для которого вводятся утверждения и доказываются теоремы, и экспериментально наблюдаемой частотой появления событий.

Другая запись теоремы Бернулли:

то есть среднее арифметическое сходится по вероятности к математическому ожиданию. Более сильным утверждением является теорема Бореля,

(1.16)

Помимо определенной выше сходимости по вероятности существует еще ряд определений сходимости. Если для последовательности случайных величин _i выполняется равенство

говорят, что последовательность сходится к числу a почти наверняка. Если же

говорят, что последовательность _i сходится к числу a в среднеквадратичном смысле и обозначают такой предел следующим образом:

3. Совместные и условные распределения.Р/м две зависимые СВ–  и . Пусть событие A заключается в том, что   x, а событие B – в том, что   y. Тогда можно рассмотреть вероятность события AB: P{AB}=P{  x,   y} = F₂(x, y). Введенная здесь функция F₂(x, y) называется двумерной интегральной функцией распределения вероятностей и обладает очевидными свойствами:F₂(x, ) = F₁(x), F₂(, y) = F₁(y), F₂(– , y) = F₂(x, – ) = 0. Если F₂(x, y) – дважды дифференцируема, можно ввести двумерную функцию плотности вероятности:

Выражения для двумерной ф-ии плотности вер-сти

где где

(1.17)

Если СВ  и  независимы, то F₂(x, y) = F₁(x)F₁(y) и ₂(x, y) = ₁(x)₁(y). Для зависимых величин  и  можно записать условную вероятность того, что одна из них находится ниже уровня y, если другая заключена в интервал Опираясь на соотношения (1.2) и (1.17), получим:

В пределе при получим

Полученная функция F₂(y| x) называется условной интегральной вероятностью распределения величины  при условии  = x. Введем также двумерную условную функцию плотности вероятности:

(1.18)

формула полной вероятности:

или

(1.19)

То. можно записать:

(1.20)

аналог формулы Байеса для двумерной условной функции плотности вероятности.

Р/м общий случай. Для совокупности из n СВ ₁,…, _n введем n-мерную интегральную вероятность

и n-мерную функцию плотности вероятности

Очевидно, для n независимых случайных величин выполняется соотношение

Если трактовать совокупность случайных величин ₁,…, _n как компоненты случайного вектора в некоторомn-мерном пространстве, можно рассмотреть событие A, заключающееся в том, что конец вектора попал в некоторую областьG этого пространства. Тогда

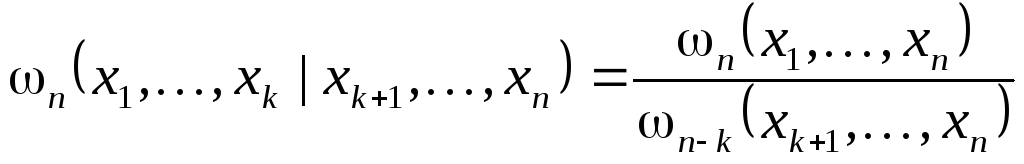
Для совокупности СВ опеделены моменты:

центральныемоменты

и смешанные моменты

Смешанный центральный момент второго порядка называется ковариацией:

Если ₁ и ₂ независимы, то cov(₁,₂) = 0. Коэффициентом корреляции R(₁, ₂) называется ковариация, нормированная следующим образом:

Ясно, что коэффициент корреляции безразмерен и |R(₁, ₂)| < 1. Если R(₁, ₂) = 0, то говорят, что случайные величины ₁ и ₂ некоррелированы. Заметим, что независимые случайные величины всегда некоррелированы, а вот обратное утверждение неверно. Случайные величины ₁ и ₂ называются ортогональными, если m₂(₁, ₂) = 0.

Вводятся условные моменты

Р/м классический пример – многомерное нормальное распределение

Здесь D – главный определитель корреляционной матрицы с элементами d_ij = R(_i, _j) = d_ji (i  j), d_ii = 1, |d_ij|  1, а D_ij – алгебраическое дополнение элемента d_ij. Можно показать, что и

Рассмотрим более подробно двумерное нормальное распределение:

(1.21)

где R = R(_i, _j). Вторые центральные моменты

Рассмотрим случайную точку на плоскости (x₁, x₂), координаты которой ₁ и ₂ – независимые случайные величины, распределенные в соответствии с функцией плотности вероятности (1.21) с нулевыми средними и одинаковыми дисперсиями . Найдем вероятность попадания

точки в круг радиуса  с центром в начале координат (рис. 1.5):

Соответствующая этой интегральной вероятности функция плотности имеет вид

(1.22)

и называется распределением Рэлея (рис. 1.6)

Рис. 1.6. Распределение Рэлея

Рис. 1.5. Случайная точка на плоскости

4. Характеристические функции По определению характеристической функцией называется среднее от комплексной экспоненты <exp(ju)>:

Характеристическая функция является Фурье-образом функции плотности вероятности ₁(x).обратное ПФ

(1.24)

Характеристическая функция ограничена по модулю:

Р/м среднее произвольной функции СВ f():

Где

–Фурье-образ исходной функции f().

Поскольку характеристическая функция, так же, как и функция плотности вероятности, однозначно описывает распределение вероятностей, с ее помощью можно найти моменты случайной величины. Р/м n-производную характеристической функции

Отсюда

Разлагая в определении характеристической функции (1.23) экспоненту в ряд по степеням x, получим:

(1.25)

Часто в ряд разлагают не саму характеристическую функцию, а ее логарифм

(*)

(1.26)

Коэффициенты ряда (*) _n() называются семиинвариантами и являются рациональными функциями моментов случайной величины . Так, например ₀() = 0, ₁() = m₁, ₂() = M₂ = ², ₃() = M₃, ₄() = M₄ – 3M₂² и т. д.

Характеристическая функция одномерного нормального распределения (1.12) равна

а все семиинварианты, начиная с номера n = 3, равны нулю. Характеристическая функция суммы независимых случайных величин  =  +  равна произведению характеристических функций _(u) = _(u)_(u), а семиинварианты равны сумме соответствующих семиинвариантов _m() = _m() + _m(). Эти соотношения позволяют записать выражения для функции плотности вероятности суммы независимых случайных величин. Поскольку Фурье-образ произведения равен свертке Фурье-образов, получаем

(1.27)

Это выражение называется формулой композиции.

Для n-мерной случайной величины можно ввестиn-мерную характеристическую функцию:

5. Центральная предельная теорема ЦПТ была доказана Ляпуновым и формулируется следующим образом: Пусть ₁,…, _N – независимые СВ, средние значения которых равны соответственно <_i> = a_i, дисперсии ограничены и равны M₂(_i) = _i² < C < . Если для любого  > 0 выполняется равенство

то случайная величина

имеет распределение, равномерно сходящееся к нормальному при N   независимо от распределения слагаемых.

Приведем доказательство ЦПТ для случая, когда все случайные величины ₁,…, _n распределены одинаково с равными средними <_i> = a и дисперсиями M₂(_i) = ². Примером такого случая может служит выборка одной случайной переменной (t). Введем новые величины _i = _i – a, для которых <_i> = 0, D(_i) = ², D(_i/N) = ²/N² = _N²/N. Теперь построим случайную величину

и запишем выражение для ее характеристической функции с учетом формулы (1.25):

При N   это выражение эквивалентно следующему:

что при N   эквивалентно выражению

Для СВ с ненулевым средним

_N = _N + a при этом имеем

Таким образом, распределение выборочного среднего случайной величины равномерно сходится к нормальному с тем же средним и дисперсией, в N раз меньшей.

Необходимым условием ЦПТ является ограниченность дисперсий исходных процессов ₁,…, _n. пример-распределение Коши

у которого не существует моментов всех четных порядков (в том числе – второго). Соответствующая этому распределению характеристическая функция равна

что для суммы N случайных величин дает

Таким образом, функция плотности вероятности суммы равна

то есть опять получается распределение Коши. Для выполнения ЦПТ часто достаточно не независимости случайных величин, а их некоррелированности или даже убывания коэффициента корреляции с достаточно высокой скоростью, то есть

6. Функция случайной величины Под функцией случайной величины (ФСВ) мы будем понимать детерминированную функцию, зависящую от какого-либо параметра (от времени, координаты и т. д.) и конечного числа случайных величин. Например

–

функция случайной величины, зависящая от времени.

Рис. 2.1. Случайная импульсная последовательность

Классическим примером ФСВ является последовательность возникающих в случайные моменты времени импульсов одинаковой формы со случайной высотой (рис. 2.1), которая может быть описана в виде

Пусть задано совместное распределение вероятностей _N(x₁,…,x_N) совокупности случайных величин ₁,…, _N и задана совокупность M однозначных непрерывных функций N переменных вида

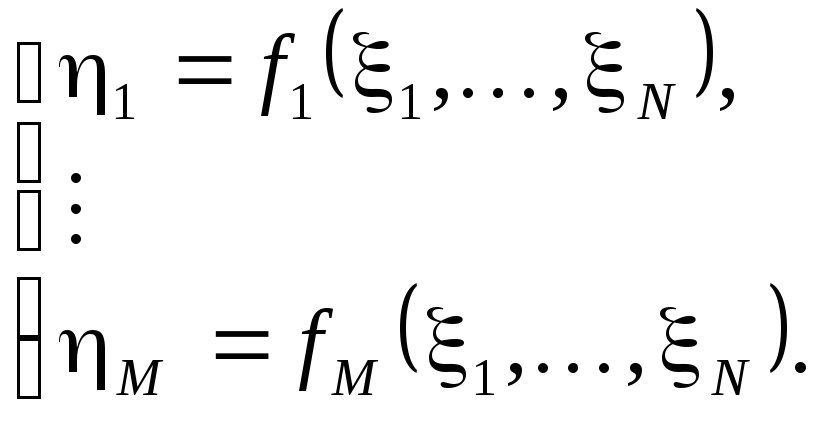
Необходимо найти совместное распределение вероятностей W_N(y₁,…,y_N) случайных величин ₁,…, _M. В одномерном случае задача сводится к нахождению распределения W₁(y) случайной величины  = f(), если известно распределение ₁(x).Рассмотрим одномерную задачу и предположим, что функция f(x) дифференцируема и существует обратная функция x = g(y), то есть связь величин  и  взаимно однозначна. Тогда, очевидно, при df/dx > 0 вероятность P{  y} = P{  x = g(y)}, а при df/dx < 0 вероятность P{  y} = P{  x = g(y)}. Используя определение функции плотности вероятности (1.6), получим:

Объединяя эти равенства, получим

В качестве примера рассмотрим линейную зависимость  = f() = a + b, где в качестве случайного выступает гауссов процесс с нулевым средним и дисперсией ² получим:

Р/м случай, когда функция y = f(x) такова, что обратная ей функция x = g(y) неоднозначна, то есть одному значению y соответствует несколько значений g(y) – x₁, x₂ и т. д.. В этом случае событию y    y + dy соответствует одно из взаимоисключающих событий: x₁    x₁ + dx₁, x₂    x₂ + dx₂ и т. д., запишем

Примером такого случая может служить квадратичное преобразование  = ², того же гауссова процесса с нулевым средним. Функция плотности вероятности процесса будет иметь вид:

Еще один вариант реализуется, когда из одной случайной величины получаются две – ₁ = f₁() и

₂ = f₂(), причем существует обратная функция  = g₁(₁). Тогда ₂ = f₂(g₁(₁)) = F(₁), а условное распределение имеет вид

что с учетом (1.20) дает возможность записать

Аналогично, если известна двумерная функция плотности вероятности (x₁, x₂) и зависимости

₁ = f₁(₁, ₂) и ₂ = f₂(₁, ₂) при наличии обратных функций (не обязательно однозначных) ₁ = g₁(₁, ₂) и ₂ = g₂(₁, ₂), двумерная функция W₂(y₁, y₂) может быть записана в виде

Здесь индекс k определяет номер неоднозначности обратных функций, а величина

-якобиан преобразования. При однозначных преобразованиях в этом выражении будет только один член.

Распределение одной СВ, являющейся функцией двух других, то есть  = ₂ = f₂(₁, ₂), положив ₁ = ₁. Тогда