20. Марковские процессы .Уравнение Смолуховского

Р/м случайный процесс (t), все конечномерные распределения которого известны. n-мерная функция распределения _n можно выразить через n–1-мерную _n–1 и одномерную условную :

Произведение (t_n, x_n| t₁, x₁,…, t_n–1, x_n–1)dx_n дает условную вероятность того, что x_n < (t_n) < x_n + dx_n, при условии, что (t_i) = x_i. Таким образом, условная вероятность для момента времени t_n определяется множеством предыдущих состояний в моменты времени t₁, …, t_n–1. Говорят, что случайный процесс испытывает вероятностное последействие со стороны своих прошлых значений. Частным случаем является процесс без последействия, когда

(t_n, x_n| t₁, x₁,…, t_n–1, x_n–1) = (t_n, x_n| t_n–1, x_n–1),

Случайные процессы, функции плотности вероятности которых удовлетворяют этому, называют марковскими процессами первого порядка. Отсюда получим

Таким образом, для полного задания функции _n марковского процесса необходимо знать только две функции плотности вероятности – _n(t₁, x₁) и (t_n, x_n| t_n–1, x_n–1). Условная функция распределения (t_n, x_n| t_n–1, x_n–1) называется вероятностью перехода из состояния t_n–1, x_n–1 в состояние t_n, x_n.

Для стационарного марковского процесса запишем

Если в качестве случайного процесса рассматривается случайная последовательность x_n = x(t_n), то для нее марковость означает, что существует вероятность перехода от любого x_i при l-м испытании к любому x_k при n-м испытании:

Если при этом случайная величина _n принимает конечное множество возможных значений, то последовательность называют простой цепью Маркова. Ясно, что для стационарной марковской последовательности вероятность перехода зависит только от сдвига индекса m = n – l, то есть от числа шагов между состояниями:

Если при дискретном времени t_n значения x случайной величины _n = (t_n) образуют непрерывное множество, то марковость процесса означает, что существуют вероятности переходов

а условие стационарности имеет вид:

Используя определение марковского процесса для момента времени t₃ запишем:

Если известно, что (t₁) = x₁, то

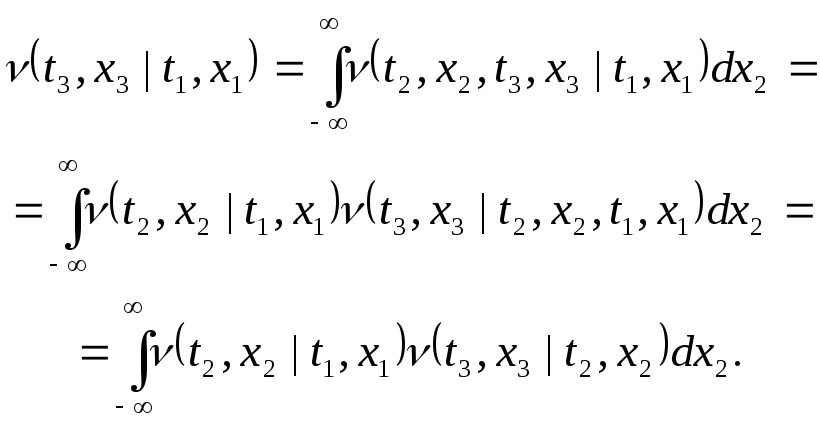
Мы получили уравнение Смолуховского:

Для дискретного множества значений x уравнение (7.6) принимает вид

Для случайной последовательности момент времени t_n надо заменить на номер шага n:

Для стационарного случайного процесса уравнение Смолуховского несколько упрощается:

21. Марковский процесс с дискретными состояниями

Р/м простую цепь Маркова, то есть марковский процесс с конечным числом дискретных состояний. Пусть в момент времени t₀ задано распределение вероятности p(t₀, x_k) = P{(t₀) = x_k}. Проследим изменение этого распределения во времени. Для этого перепишем уравнение Смолуховского для моментов времени

t₀ < t < t + 

и предположим, что при достаточно малых  вероятность перехода пропорциональна , то есть

Такая запись позволяет получить верное исходное распределение при   0:

(7.10)

Вероятность перехода за время  из состояния j в состояние k  j определяется выражением

Очевидно, что для любого времени  на основе условия нормировки можно записать

поэтому с учетом выражения (7.9)

(7.11)

Поскольку по смыслу вероятности все A_jk > 0 (k  j), величины A_jj < 0.

Рассматривая предел при   0, получим:

Полученная система уравнений определяет динамику вероятностей переходов. Выбрав по другому три момента времени t₀ < t₀ +  < t, можно получить аналогично

В тех случаях, когда нас интересует динамика вероятностей состояний p(t,x_k), можно поступить следующим образом. Используя формулу полной вероятности

и подразумевая в ней под событием B событие (t) = x_k, а под событием A_i – (t₀) = x_i, запишем:

получим следующее уравнение

Вместе с начальным условием p(t₀,x₀) оно определяет динамику распределения вероятностей.

Если марковский процесс стационарен, вероятность перехода зависит только от временного сдвига, то есть

В этом случае выражение (7.12) примет вид

В качестве примера рассмотрим задачу об определении динамики вероятностей переходов в двухуровневом лазере. Предположим, что вероятности переходов с уровня 1 на уровень 2 и обратно за время dt пропорциональны этому времени, то есть

A₁₂dt = dt, A₂₁dt = dt.

можно вычислить величины A₁₁ и A₁₂:

Теперь можно записать систему уравнений:

Поскольку из условия нормировки p(t, 1) + p(t, 2) = 1, полученная система сводится к уравнению

для решения которого необходимо задать начальные условия. Пусть в момент времени t = 0 уровень два полностью заселен, а уровень 1 – пуст. Тогда p(0, 1) = 0, p(0, 2) = 1, а решение полученного уравнения имеет вид

Стационарное распределение вероятностей получается из этих соотношений при t  :