33. Анализ случайной дифракции методом мма

В общем случае связь между поляризацией и вектором поля следует записать в виде интеграла Дюамеля

где – тензор диэлектрической восприимчивости.

Будем искать решение волнового уравнения (10.2) в виде плоской квазимонохроматической волны, распространяющейся вдоль оси z:

В этом выражении k₀ – значение волнового вектора, направленного вдоль оси z, а e – орт, перпендикулярный этой оси. Если среда однородна, для поляризации можно записать

Если изменение амплитуды волны за время порядка 1/₀ мало, то есть

комплексную амплитуду A(z, t – ) можно разложить в ряд по степеням  вблизи точки t. Тогда выражение для поляризации примет вид

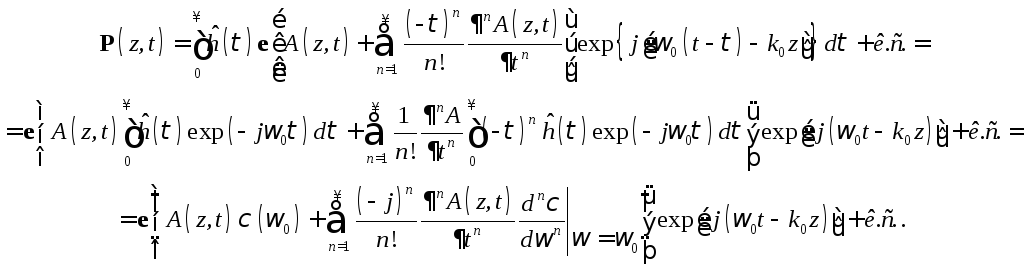Здесь введено обозначение

восприимчивость на частоте . Таким образом

В первом приближении при слабой дисперсии выражение для поляризации примет вид

Вычислим входящую в уравнение (10.2) вторую производную поляризации, пренебрегая второй производной комплексной амплитуды A(z, t) – это можно сделать, поскольку мы находимся в рамках метода ММА.

Найдем также производные поля E(z, t),

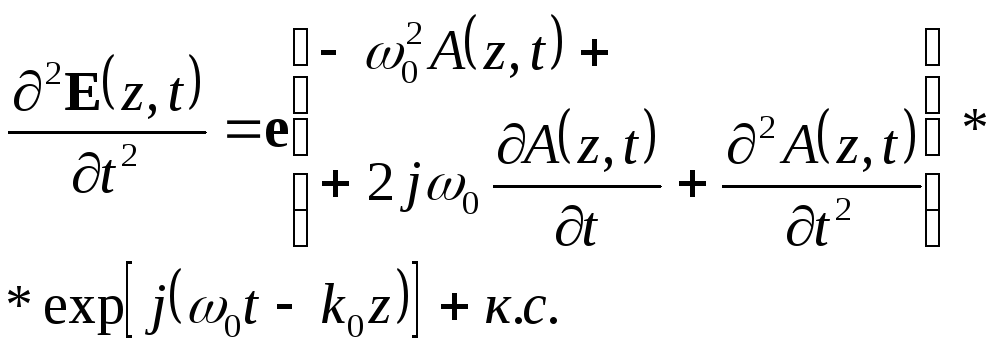
ограничиваясь только первыми производными амплитуды поля (поскольку она медленно меняется), получим

Если восприимчивость () является чисто действительной величиной (это соответствуют среде без потерь), то дисперсионное соотношение, связывающее k и :

Если ввести показатель преломления , полученное уравнение примет вид

Дифференцируем по частоте , получим

где u = [dk/d]^–1 – групповая скорость.

Выделяя мнимую и действительную часть, получим уравнение для амплитуды

общее решение которого имеет вид волны:

(10.13)

Величина A₀ определяется граничными условиями. Если волна монохроматическая, значит – и

Таким образом амплитуда поля A(z, t) = const, что вполне логично, поскольку мы пренебрегли потерями в среде, взяв действительную восприимчивость ().

Р/м теперь среду с потерями. В этом случае восприимчивость следует записать в виде () – j()/(4), тогда для монохроматической волны при

мнимая часть уравнения (10.10) дает

Считая потери не зависящими от частоты, получим, что дисперсионный и диссипативный члены входят аддитивно. Тогда, получим

Р/м еще один случай, когда потерь в среде нет, а распространяющаяся в ней монохроматическая волна характеризуется частотой  = ₀ + . Тогда ее комплексную амплитуду можно представить в виде

Можно сделать вывод, что добавка q к волновому числу k₀ составляет q = /u = dk/d, а само волновое число на частоте  = ₀ +  равно k(₀ + ) = k(₀) + /u. Таким образом, уравнение (10.12) справедливо в случае, когда дисперсию среды можно считать линейной.

Если линейной аппроксимации поляризации недостаточно, Так, во втором приближении выражение для поляризации и ее второй производной имеют вид

получим уравнение для комплексной амплитуды

С учетом (10.12) можно записать для второго члена этого уравнения

Соответственно, уравнение для комплексной амплитуды упростится

где –дисперсия групповой скорости. Подставив (10.15) в это уравнение, получим

Таким образом, дисперсионные свойства среды описываются квадратичной зависимостью.