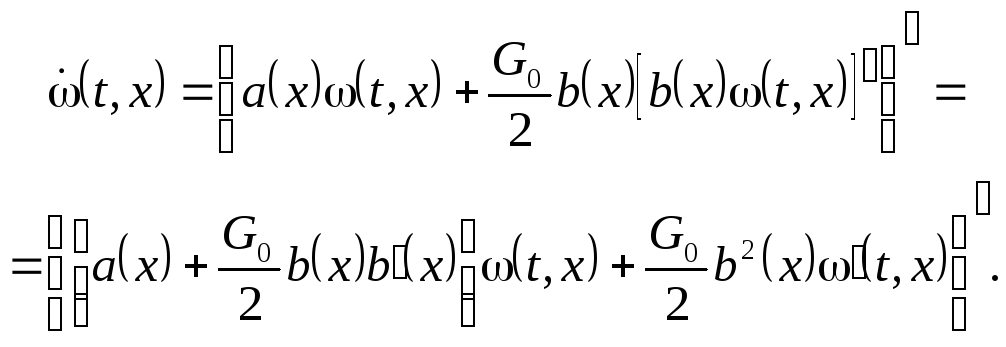26. Уравнение для средних и его связь с уравнением фпк.

Р/м нелинейное дифференциальное уравнение первого порядка с переменными коэффициентами:

(8.15)

полагая, что случайный процесс (t) – белый шум, то есть

Пусть функция x(t) является решением уравнения (8.15). Рассмотрим вспомогательную задачу – найдем функцию [x(t)] такую, что

где f[x(t)] = f(t) – некоторая функция запаздывающего потенциала. Для любого момента времени t и для любого  > 0 можно представить функцию f[x(t)] в виде

По принципу причинности f[x(t – )] может зависеть только от значений процесса (t  t – ), кроме того, в силу дельта-коррелированности процесса (t) значение f[x(t – )] не коррелирует с (t). Таким образом, в среднее <f[x(t)](t)> может внести вклад только коррелированная компонента f_k(t), то есть

где

Из-за инерциальности системы, x(t), а значит – и функции a(x) и b(x), должны меняться медленно по сравнению с белым шумом (t). Это означает, что коррелировать с белым шумом может только один член предыдущего уравнения, а именно b(x)(t). В силу произвола  выберем его много меньшим интервала корреляции процесса x(t), то есть  << _k(x). Тогда можно утверждать, что функции df/dx и b(t) на интервале интегрирования [t – , t] и в некоторой его окрестности практически постоянны и можно записать

Как уже упоминалось, в силу дельта-коррелированности процесса (t) как сам процесс (t), так и его интеграл не коррелируют с произведением

поэтому

Здесь учтено

Таким образом, если положить, что

получим

Р/м теперь среднее от производной по времени произвольной функции F[x(t)] = F(x) = F(t), С одной стороны по определению производной

С другой стороны, в соответствии с уравнением (8.15), получим

Полагая в выражении (8.17)

запишем

дифференциальное уравнение для среднего функции F(x). В частности, при F(x) = x уравнение (8.20) превращается в уравнение для <x(t)> = m₁(t):

Если Ур-

его коэффициенты равны a(x) = ax – f₀(t) и b(x) = bx, а уравнение является уравнением со случайным коэффициентом. Тогда уравнение для первого момента принимает вид

или по-другому

Решение этого уравнения может быть записано в виде интеграла Дюамеля:

Уравнение для средних (8.20) часто удобнее записывать в другом виде. Вычислим его компоненты, учитывая, что (t, ) = 0:

_{Получаем}

причем

Если выбрать F(x) = (x – x₁), то

Тогда

Если это уранение переписать в виде

получим уравнение ФПК и, главное – связь коэффициентов сноса и диффузии с коэффициентами уравнения:

27. Уравнение Лиувилля.Случайный телеграфный сигнал.

Р/м решение нелинейного уравнения для x(t), считая, что случайный процесс (t) не обязательно является белым шумом. Выберем в качестве функции [x(t)] = [x(t) – s], где s – некоторая константа. Тогда

В силу свойств -функции b(x)(x) = b(s)(x) = b_s(x) и a(x)(x) = a(s)(x) = a_s(x), поэтому

- уравнением Лиувилля. Усредним его, учитывая, что s, b_s и a_s не являются случайными величинами:

Учитывая, что

получим

усредненное уравнение Лиувилля. В частном случае, когда (t) – белый шумовой процесс, учитывая выражение (8.17), вычислим коррелятор

подставив который в выражение (8.24), получим

уравнение ФПК.

Случайный телеграфный сигнал …

Ра/м методы решения стохастических дифференциальных уравнений высокого порядка путем их сведения к системе уравнений первого порядка. Рассмотрим уравнение вида

где (t) – белый шум с нулевым средним. Обозначим и перепишем уравнение в виде

или, в соответствии с формой (8.15)

где b(x) = 1 – x – x₁ – x₂. Усредним полученное уравнение

Вычисляем корреляторы этого Ур-ия:

Подставив корреляторы и возвращаясь к производным x(t), получим уравнение для средних: