Курнаев Введение в пучковую електронику 2008

поток энергии пропорционален T 4. Максимальные значения Sv достигаются при lv ≈ L′. Закономерности формирования оптического спектра lv обсуждаются ниже.

1.4.3.Термоэлектрические, гальваномагнитные

итермомагнитные явления

Кинетические явления в кристаллах, обусловленные изменением функции распределения электронов при одновременном воздействии нескольких возмущающих факторов – электрического и магнитного полей и градиента температуры, – по типу действующих сил подразделяют на три основные группы: термоэлектрические, гальваномагнитные и термомагнитные.

Термоэлектрические явления

Термоэлектрические явления объединяют группы физических процессов, обусловленных взаимными превращениями энергии теплового движения и энергии электрического тока. К ним относят обычно три обратимых эффекта – Зеебека, Пельтье и Томсона.

Эффект Зеебека

Эффект Зеебека заключается в том, что в электрической цепи, состоящей из последовательно соединенных элементов, изготовленных из различных материалов, возникает термоЭДС, если места контактов поддерживаются при неодинаковых температурах. Если при j = 0 в однородном образце rT ≠ 0 , то возникает поле напря-

Если соединить два различных металла (полупроводника) А и В в замкнутую цепь и поддерживать контакты 1 и 2 под разными температурами, то в цепи возникает ЭДС ϕ:

ϕ = ∫ EBdx + ∫ EAdx + ∫ EBdx = ∫(QA −QB )dT .

101

На количественные характеристики эффекта Зеебека влияет изменение распределения температуры, сечений соударений, градиентов температуры и др.

Эффект Пельтье

Эффект Пельтье, обратный эффекту Зеебека, состоит в том, что при прохождении тока в цепи с проводниками из разнородных материалов в местах контактов помимо выделения джоулевой теплоты поглощается или выделяется (в зависимости от направления тока и типа вещества) некоторое количество теплоты Qn = ΠIt , где

П – коэффициент Пельтье; I – сила тока; t – время. Если вдоль подобной цепи поддерживается постоянная температура, T = 0 , и под действием внешней ЭДС протекает ток j, то

С учетом определения Kn , легко заключить, что Π зависит от материала и состояния (температуры) проводника, т.е. в ветви А течет поток теплоты ΠA j , в ветви B − ΠB j ≠ ΠA j . На контактах

поток теплоты должен быть непрерывен; следовательно, количество теплоты, равное (ΠA − ΠB ), выделяется в единицу времени на

одном контакте и поглощается на другом. В нагреве одного контакта и охлаждении другого и состоит эффект Пельтье. Из (1.45) и (1.47) видно, что

Эффект Томсона

При наличии в цепи одновременно и электрического тока, и потока теплоты в объеме однородного проводника на фоне выделения джоулевой теплоты при j rT < 0 поглощается, а при j rT > 0 вы-

деляется количество теплоты

102

где τ = τ(T ) – коэффициент Томсона. Из (1.45), (1.49) следует связь

τ и Q:

Коэффициент Томсона имеет физический смысл удельной теплоемкости носителей электрического тока: количество теплоты поглощается, если потоки теплоты (из-за теплопроводности и носителей заряда) противонаправлены, и выделяется, если они сонаправлены, т.е. поток носителей заряда как бы сносит тепловое распределение с собой.

ТермоЭДС электронного газа

Значение термоЭДС (и связанных с Q коэффициентов Пельтье (1.48) и Томсона (1.50)) зависит от особенностей рассеяния носителей заряда и дисперсионных зависимостей вблизи E = EF . Учиты-

вая выражения для σ и термоЭДС Q через интегралы Kn (1.45), (1.46) и определение Kn , получают связь между Q и σ в виде

В зависимости от знака носителей заряда может быть взят плюс или минус; σ = σ(E) рассматривается как функциональная зависи-

мость σ от энергии Е, соответствующей поверхности S:

σ = σ(E)= 1 (4π3 ) (e2τ=)∫l (E)dS (E).

Непосредственно выражение (1.51) применимо при T ≥ ΘD . Аппроксимируя зависимость σ = σ(E) вблизи E = EF степенной зависимостью

σ = const Ex ,

В зависимости от особенностей рассеяния и строения электронного спектра вблизи E = EF величина х может быть положитель-

ной или отрицательной. В переходных металлах энергия Ферми лежит в области d-полос, дающих основной вклад в плотность со-

103

стояний dζ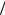dE (Ed − EF ). В терминах квазичастиц m* < 0 (рас-

сматривается верх разрешенной зоны, см. разд. 1.2), т.е. носители заряда ведут себя как дырки. Если считать, что особенности поведения σ(E) определяются особенностями энергетической зависи-

Поскольку Ed − EF << EF , для переходных металлов значение Q больше, чем для простых.

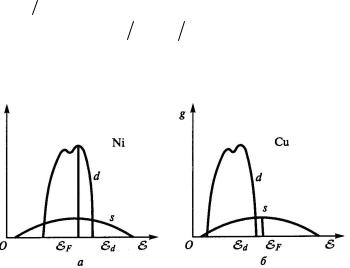
Рис. 1.87. Плотность состояний никеля (а) и меди (в)

Выражение (1.53), как и (1.52), получено в достаточно грубых приближениях и может лишь с осторожностью применяться в количественных расчетах; в частности, оно не точно при температурах меньше температуры магнитного упорядочения. Однако (1.53) качественно верно описывает влияние уровня Ферми на Q, в частности, для сплавов переходных и непереходных металлов, например Cu-Ni-сплавов. Размеры и электроотрицательность атомов Cu (атомный номер 29) и Ni (28) очень близки, и они образуют гомогенные твердые растворы замещения при любых концентрациях. Однако в среднем 0,6 электронов на атом Ni в чистом металле уходят из d-оболочек и находятся в s-состоянии, оставляя 0,6 дырок в d-оболочке на атом, т.е. энергия Ферми лежит ниже Ed , у чистой

меди же каждому атому соответствует один свободный s-электрон, а d-оболочка полностью занята (рис. 1.87). В сплаве часть электронов меди заполняют дырки в d-оболочках никеля, приближая EF к

104

Ed . Согласно (1.53), это должно вызвать рост термоЭДС, что и на-

блюдается в эксперименте. Максимум на зависимости Q от концентрации связан с конкуренцией роста Q, согласно (1.53), и влиянием разбавления переходного элемента с увеличением концентрации Cu.

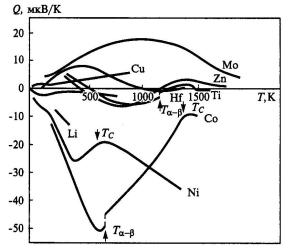
На рис. 1.88 показаны экспериментальные термоЭДС для ряда металлов.

Рис. 1.88. Температурная зависимость абсолютной термоЭДС некоторых металлов

Электронная термоЭДС в полупроводниках имеет гораздо большие значения, чем в металлах, так как электронный газ не вырожден, и температурные изменения функции распределения значительнее.

Решеточная термоЭДС

Наряду с потоком заряда и электронной термоЭДС может проявляться поток теплоты, переносимый «увлеченными» фононами – решеточная термоЭДС. Причина «увлечения» фононов – передача им импульса при электрон-фононных рассеяниях, преимущественно в направлении дрейфа носителей заряда, в ходе нормальных процессов, для которых суммарный импульс сохраняется. Эту кар-

105

тину существенно нарушают процессы переброса, при которых фононы испускаются более всего в направлении, противоположном направлению тока носителей заряда.

Особенно значительна роль переброса в металлах, так как в вырожденном электронном газе переходы с малым изменением энергии происходят при начальном и конечном состояниях электрона вблизи поверхности Ферми, которая может быть близка к границам зоны Бриллюэна, так что относительно малого импульса фонона достаточно для выхода за пределы этой зоны, т.е. для осуществления процесса переброса.

В невырожденных полупроводниках при T << ΘD возбуждают-

ся акустические фононы также с малыми волновыми числами, и процессы переброса происходят редко. В полупроводниках термоЭДС значительно выше, чем в металлах. Знак решеточной термоЭДС совпадает со знаком носителя заряда.

Гальваномагнитные явления

Гальваномагнитные явления – это совокупность эффектов, связанных с воздействием магнитного поля на электрические свойства твердых тел.

Электропроводность анизотропного кристалла является в общем случае тензором, и гальваномагнитные явления можно трактовать как изменение этого тензора под действием магнитного поля, приводящего к искривлению траекторий электронов между столкнове-

ниями с радиусом кривизны r = m*vдр 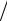(eB0 ). Особенно сильно

сказывается влияние магнитного поля при критических значениях индукции B0 , когда радиус r становится величиной одного порядка

с длиной свободного пробега le . В этом случае искажение траекто-

рии настолько велико, что изменяется механизм рассеяния электронов. Критическая напряженность поля для большинства ве-

ществ очень высока ( Hкр ≈107...1011 А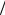м ), и в реальных полях

( H =106 А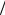м) искривление траекторий электронов незначительно. Однако у ряда веществ (например, в Bi) значение Hкр значительно ниже и магнитное поле резко изменяет тензор электропроводности.

106

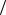
Гальваномагнитные явления подразделяют на продольные и поперечные в зависимости от того, в каком направлении они проявляются относительно вектора электрического поля. К поперечным гальваномагнитным явлениям относят эффекты Холла и Эттинсгаузена, к продольным – изменение продольного сопротивления в магнитном поле и эффект Нернста.

Эффект Холла

Эффект Холла заключается в возникновении поперечного электрического поля EH в кристалле, по которому протекает ток I, при помещении его во внешнее магнитное поле В0, перпендикулярное I. Поле EH перпендикулярно I и В0, а его напряженность

пропорциональна силе тока и индукции магнитного поля. Физическую природу эффекта Холла легко понять с помощью

кинетического подхода, анализируя движение свободных электронов в скрещенных электрических и магнитных полях (как в газовой плазме). Известно, что в поле на движущуюся частицу действует сила Лоренца Fл = e[B, v], перпендикулярная скорости. Чтобы

скомпенсировать вызванное этой силой отклонение носителей заряда, требуется наложение поперечного электрического поля

возникающего в результате появления нескомпенсированных зарядов на поверхности тела. Две указанные поперечные силы компенсируют одна другую, и носители тока движутся под действием лишь продольного электрического поля.

ЭДС Холла обратно пропорциональна концентрации n носителей тока, поскольку при той же плотности тока с падением n растет средняя скорость, т.е. увеличивается относительное влияние магнитных сил.

Имеется и качественное, и количественное соответствие между проявлениями эффекта Холла в плазме твердого тела и в газовой плазме: формула (1.54) применима в обоих случаях. Если B j , то

поперечное поле (поле Холла) FH = e τjB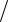(m*σ)= RjB , коэффици-

ент Холла в данном приближении FH = e τ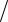(m*σ)≈1(ne). При вы-

107

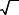
ходе за рамки модели свободных электронов появляется зависимость R от особенностей поверхности Ферми и индукции магнитного поля, наиболее заметная при низких температурах. B ферромагнетиках ЭДС Холла определяется суммой R0 B + Rs I , где R0 –

обычный, или нормальный, коэффициент Холла; В – индукция магнитного поля; Rs – аномальный коэффициент Холла; I – намагниченность образца. При комнатных температурах в ферромагнетиках Rs на один-два порядка больше R0 и существенно зависит от температуры (часто наблюдается корреляция между поведением Rs и квадратом электросопротивления). Ниже приведены данные

для коэффициента Холла в парамагнитной области.

У металлов значение R имеет порядок 1010 м3/Кл, эффект Холла проявляется слабо, аномально большие значения постоянной Холла имеют металлы V группы (Bi, Sb, As) – до 10–6 м3/Кл. У полупроводников R достигает 102 м3/Кл. При наличии носителей заряда обоих знаков R = (A/e)(nhμh2 − neμe2 )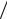(μhnh + μene )2 .

При рассмотрении эффекта Холла в полупроводниках следует учитывать зависимость длины пробега l электронов от энергии (так как перенос осуществляется электронами с широким спектром Е):

R = ± A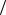(en),

где А – постоянная, учитывающая энергетическую зависимость l, А ~ 1 для вырожденного газа, а для невырожденного

A = 34 πΓ(2r +3/2)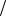[Γ(r + 2)]2 ;

здесь Г – гамма-функция, r имеет то же значение, что и в (1.54); так, для рассеяния на ионах (r = 2) А = 1,93.

Плотность тока связана с параллельной составляющей электрического поля:

E|| = j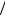σ.

Для дырок справедливы аналогичные закономерности, но из-за другого знака заряда (или mh* ) направление ЭДС Холла противоположно.

108

Эффект Эттинсгаузена

Эффект Эттинсгаузена заключается в появлении поперечного градиента температуры при протекании тока I в магнитном поле B I . Причина в том, что реальный электронный газ в кристалле имеет некоторое распределение по скоростям, на более быстрые электроны действует большая отклоняющая сила магнитного поля, и они могут преодолеть силы поперечного электрического поля Холла. Медленные электроны, на которые действует меньшая отклоняющая сила Лоренца, не могут преодолеть силу eEH и сме-

щаются к противоположной стенке образца. В результате происходит разделение электронов в поперечном направлении в зависимости от их скорости, и вследствие обмена энергией электронов с решеткой (быстрые электроны отдают энергию, а медленные увеличивают ее за счет решетки) в поперечном направлении появляется градиент температуры T = P[I,B0 ] , где Р – коэффициент Эттинс-

гаузена. Поперечный перепад температур невелик (обычно он не превышает долей градуса).

При помещении вещества в магнитное поле изменяется продольная составляющая электропроводности. Это явление называют магнитосопротивлением (магниторезистивным эффектом, эф-

фектом Гаусса). Магнитное поле вызывает искривление траекторий электронов проводимости, и если вдоль искривленной траектории длина свободного пробега останется прежней, то в направлении электрического поля она уменьшится, а следовательно, уменьшится и электропроводность; ее изменение связано с индукцией магнитного поля и подвижностью носителей заряда соотно-

шением Δσ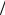σ = −C (μn B0 )2 . Магнитосопротивление в отличие от эффекта Холла является четной функцией относительно магнитного поля (изменение направления вектора B0 на противоположное не влияет на Δσ ). Коэффициент С определяется механизмом рассеяния носителей заряда и равен (9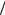16)π для ионных кристаллов. Для

109

Значение Δσσ для металлов невелико, однако у Bi это отноше-

ние может достигать 200 %, и по его изменению измеряют магнитные поля. Для полупроводников отношение Δσ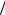σ изменяется в широких пределах в зависимости от их типа (от средних значений

10−2...10−10 до нескольких единиц). B полях напряженностью выше 106 А/м зависимость Δσ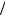σ от В0 отклоняется от квадратичной, и

Δσ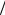σ пропорционально B0m , где 1 < m < 2.

Распределение электронов по скоростям сказывается на степени их смещения магнитным полем. Медленные электроны сильно «закручиваются» и не могут пройти вдоль всего образца в отличие от более быстрых электронов, создается продольный градиент темпе-

ратуры ∂T∂x , пропорциональный B02y Ix (эффект Нернста).

Термомагнитные явления

К термомагнитным явлениям относят эффекты, возникающие при воздействии магнитного поля на вещество, в котором существует градиент температуры. Здесь также выделяют продольные и поперечные эффекты (по отношению к направлению градиента температуры).

B кристалле с разными температурами граней встречные диффузионные потоки носителей заряда отклоняются магнитным полем в разные стороны, а поскольку они имеют разные тепловые скорости, появляется поперечный градиент температуры (эффект Риги – Ледюка). Кроме того, более быстрые электроны, движущиеся от горячей грани, слабее отклоняются полем, тогда как движущиеся им навстречу от холодной грани медленные электроны получают большее смещение, создавая поперечный градиент концентрации и поперечное электрическое поле (поперечный эффект Нернста – Эттинсгаузена). Так как искривление траекторий в магнитном поле приводит к уменьшению длины свободного пробега вдоль образца, уменьшается и продольная составляющая электронной теплопроводности (эффект Маджи – Риги – Ледюка). Искривление траекторий сказывается также на средней энергии электронов, в результате изменяется термоЭДС (продольный эффект Нернста – Эттинсгаузена).

110