
Курнаев Введение в пучковую електронику 2008
.pdf
Из анализа (1.4) следует также, что кривая E = E(k) имеет разрывы при значениях k, кратных π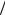 a ; это условие соответствует целому числу длин волны де Бройля, укладывающихся на длине постоянной решетки: nλB
a ; это условие соответствует целому числу длин волны де Бройля, укладывающихся на длине постоянной решетки: nλB 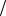 2 = a (n =1, 2, 3, ...), что совпадает с форму-
2 = a (n =1, 2, 3, ...), что совпадает с форму-
лой Вульфа – Брэгга, описывающей брэгговское отражение лучей от плоскостей кристаллической решетки; такая волна не может распространяться в кристалле из-за отражения.
Области значений k между точками брэгговского отражения называют зонами Бриллюэна. Для рассмотренной одномерной це-
почки атомов |
первая зона Бриллюэна заключена в пределах |
−π a < k < π a , |
вторая в пределах π a < k < −π a и −2π a < k < −π a |
и т.д. (представление расширенных зон Бриллюэна, рис. 1.5, а).
Из (1.4) видно, что E является периодической функцией от k с периодом 2 π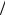 a , т.е. зависимость E(k) неоднозначна, а форма кри-
a , т.е. зависимость E(k) неоднозначна, а форма кри-
вых зависимости E(k) для первой зоны Бриллюэна полностью повторяется при сдвиге на n2π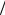 a (рис. 1.5, б – представление повторяющихся зон), т.е. первая зона Бриллюэна содержит всю информацию о зависимости E = E(k). Это позволяет выразить энергию электрона, находящегося в любой зоне Бриллюэна, через значение k, лежащее в пределах первой зоны.
a (рис. 1.5, б – представление повторяющихся зон), т.е. первая зона Бриллюэна содержит всю информацию о зависимости E = E(k). Это позволяет выразить энергию электрона, находящегося в любой зоне Бриллюэна, через значение k, лежащее в пределах первой зоны.
С ростом энергии E электрона ширина разрешенных зон увеличивается, а запрещенных уменьшается. Это соответствует более сильному расщеплению верхних, наружных, состояний электронов.
Прежде чем переходить к реальному трехмерному случаю, полезно рассмотреть еще одну гипотетическую двумерную решетку, например гексагональную.
Рис. 1.5. Различные варианты представления зонной структуры: а – представление расширенных зон Бриллюэна, б – повторяющихся, в – приведенных (цифры – номера зон)
11
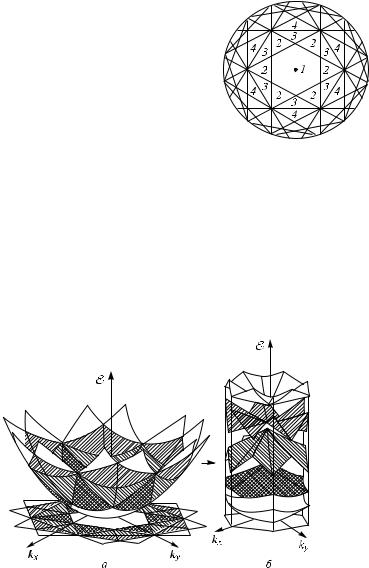
Границы зоны Бриллюэна (в представлении расширенных зон),
соответствующие условию полного брэгговского отражения в (kx , ky )-
пространстве, показаны на рис. 1.6. На рис. 1.7 изображена параболи-
ческая зависимость E =k2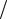 (2m) для
(2m) для
свободных электронов. Рассмотрение двумерного анало-
га модели Кронига – Пенни дает «сглаживание» резких «складок» на
поверхностях зависимости E = E(k), приведенной к первой зоне Бриллюэна (рис. 1.8), что может приводить, в частности, к появлению запрещенных зон, как и в одномерной модели. Однако возможным становится и такой случай, когда запрещенная зона для движения в одном направлении не совпадает с запрещенной зоной для движения в другом, в результате в суммарном энергетическом спектре запрещенная зона пропадает из-за перекрытия двух разрешенных зон.
Рис. 1.7. Параболоид энергии для свободного электрона (E ~ k2) над двумерной гексагонной решеткой в k-пространстве (а); приведение параболоида к первой зоне Бриллюэна (б). Параболоид и k-плоскость разделены на зоны Бриллюэна в соответствии с рис. 1.6
12
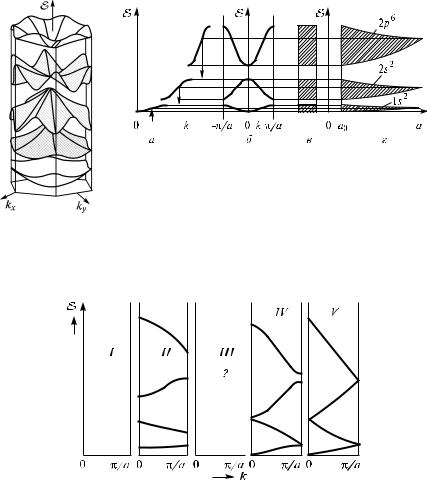
Рис. 1.8. Дисперсионная зависимость для двумерной гексагональной решетки
Рис. 1.9. Дискретные уровни изолированного атома и зоны Бриллюэна в кристалле: а – дисперсионная зависимость в приближении расширенных зон; б – приведенная к первой зоне; в – энергетический спектр разрешенных и запрещенных зон; г – уширение уровней при сближении атомов
Рис. 1.10. Иерархия дисперсионных зависимостей: I – свободные атомы; II – сильная связь; III – реальная ситуация; IV – почти свободные электроны; V – свободные электроны
Так как энергетические зоны можно представить как результат уширения уровней при сближении атомов (рис. 1.9) и имеется соответствие между дискретными состояниями изолированного атома и зонами Бриллюэна в твердом теле (рис. 1.10), считают, что одна зона происходит от 1s-состояний, одна – от 2s-, три – от 2p-, одна – от 3s-, пять – от 3d и т.д.
13
Приближения сильной связи и почти свободных электронов
Среди методов определения электронной структуры наиболее простыми являются методы, основанные на представлении периодического поля кристалла как малого возмущения. Если искажение атомных орбиталей при образовании кристалла не очень велико, то в реальных расчетах может применяться приближение сильной связи, в котором как исходные используются волновые функции изолированных атомов, а взаимодействие атомов в кристалле рассматривается как возмущение. В варианте этого приближения применяют в качестве волновых функций линейные комбинации атомных s-, p-, d-орбиталей (метод ЛКАО).
Противоположным предельным приближением, справедливым при большом перекрытии волновых функций, является метод почти свободных электронов (ПСЭ), где предполагается, что периодический потенциал создает малое возмущение соответствующих свободным электронам волновых функций, а потому именно они принимаются за нулевое приближение.
1.1.2. Движение электронов под действием внешних сил в кристалле
На основе дисперсионных зависимостей описаны характеристики движения электронов в твердом теле: динамические (скорость, эффективная масса, импульс) и статические (изоэнергетические поверхности, плотность состояний в пространстве энергии), определяющие транспортные свойства твердых тел.
Движение электрона в кристаллах, где на его состояние помимо внешнего поля существенно влияют взаимодействия с другими частицами, отличается от движения свободного электрона. Однако для описания поведения электрона в твердом теле уравнение движения удобно представить так же, как и для свободного электрона, т.е. в виде второго закона Ньютона.
При движении в силовом поле F скорость изменения энергии частицы
dE dt = Fvгр, |
(1.5) |
14

где vгр – скорость частицы, соответствующая групповой скорости волнового пакета:
vгр = kω |
(1.6) |
( k – набла-вектор в k-пространстве; ω = E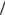 = – круговая частота колебаний). С учетом (1.5), (1.6) ускорение частицы
= – круговая частота колебаний). С учетом (1.5), (1.6) ускорение частицы
vгр 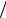 dt = d ( k E
dt = d ( k E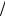 =)
=)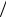 dt =(1
dt =(1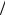 =) k dE
=) k dE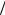 dt =(1
dt =(1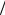 =) k Fvгр =
=) k Fvгр =
= |
1 =2 |
) |
|
k |
(F |
k |
E)= |
1 =2 |
)∑ |
e |
∂ |
|
∑ |
F |
j |
∂E ∂k |
|
∂k |
i |
= |
|
( |
|
|
|
( |
i |
|
|
|
|
j |
|
|
|||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
l |
|
|
|
|
|
|
|
=∑ei ∑Fj∂2 E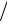 (∂k j∂ki )
(∂k j∂ki )
il
Таким образом, вектор ускорения имеет компоненты
a =∑Fj (∂2 E (∂k j∂ki )) =2 . |
(1.7) |
l |
|
Сравнение (1.7) со вторым законом Ньютона показывает, что тензор с компонентами
my =2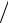 ∂2E
∂2E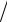 (∂k j∂ki )
(∂k j∂ki )
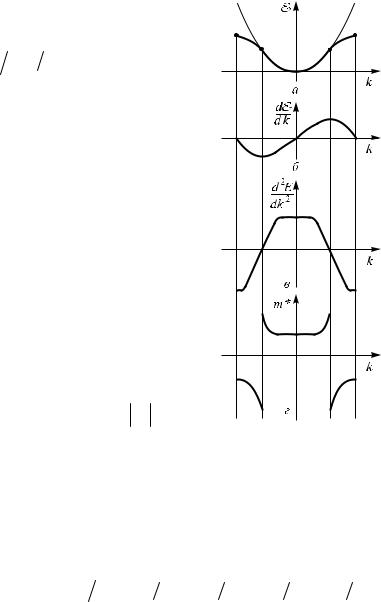
имеет размерность массы; его называют тензором эффективной массы для электрона в периодическом поле (рис. 1.11). В твердых телах с сильной анизотропией все компоненты этого тензора отличны от нуля.
Так, в Ge и Si зона проводимости (рис. 1.12) описывается двумя значениями масс me* и me*|| :
E (k)= =2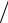 2 (kx2 +ky2 )
2 (kx2 +ky2 )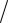 me* +kx2
me* +kx2 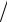 me*|| .
me*|| .
Это уравнение эллипсоида вращения с большой полуосью, расположенной в Ge вдоль направления [111] и в Si вдоль [100]. Малая полуось эллипсоида располагается в произвольном направлении в перпендикулярной плоскости, например [001] и [010] в Si и [110] и [112] в Ge.
В ряде случаев (например, для кристаллов с кубической симметрией) обоснованно приближение изотропного твердого тела,
для которого my = 0 при i ≠ j , а диагональные компоненты my
15
равны; тогда электрон имеет скаляр-
ную |
эффективную |
массу |
|
m* ==2 |
(∂2E ∂k2 ) |
(m* |
учитывает |
e |
|
e |
|
влияние сил взаимодействия электрона с кристаллической решеткой на характер его движения, но не является мерой его инерции). Введение понятия эффективной массы – прием, который позволяет решать задачи о движении электрона в твердом теле с помощью формул для свободного движения.
Понятие о дырках
Для электронов в кристаллах сила F имеет электромагнитную природу. Это позволяет при рассмотрении состояний электронов у потолка разре-
шенной зоны (me* < 0) вместо отрица-
тельной me* ввести понятие дырки – квазичастицы, имеющей положительный заряд и массу, равную me* . Удоб-
ство такого подхода состоит в том, что в области тепловых скоростей, когда
me* =const , дырки движутся аналогич-
но свободным частицам, что облегчает анализ.
Рис. 1.11. Зависимость от волнового числа: а – энергии; б – скорости (~ dE/dk); в – d2E/dk2; г – эффектив-
ной массы электронов
(~ dk2/d2E)
Таблица 1.1
Относительные массы частиц в Ge и Si
Полупроводник |
m* |
m* |
m* |
m* |
m* |
m* |
m* |
m* |
m* |
m* |
|
|| |
e |
|
e |
h1 |
e |
h2 |
e |
h3 |
e |
Ge |
1,58 |
0,08 |
0,33 |
0,042 |
0,077 |
|||||
Si |
0,91 |
0,19 |
0,49 |
0,16 |
0,245 |
|||||
16
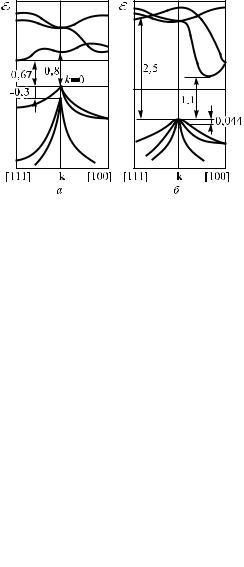
Рис. 1.12. Зависимость E(k) для трех валентных зон и нескольких первых зон проводимости Ge (а) и Si (б)
Эффективные массы электронов и дырок в общем случае не совпадают друг с другом; в реальных кристаллах возможно наличие ряда зон с экстремумами при близких энергиях (см.
рис. 1.12), т.е. одно-
временно могут существовать «тяжелые» и «легкие» электроны и дырки. Так, валентная зона Ge и Si состоит из трех подзон с тремя сортами дырок (табл. 1.1).
Изоэнергетические
поверхности
Рис. 1.13. Примеры изоэнергетических поверхностей: а – замкнутая; б – открытая в направлении ky; в – открытая в направлениях kx , ky , kz
Значения импульса (волновых векторов), соответствующие одному значению энергии, могут быть найдены
по |
зависимостям |
E = E(k). |
Так, |
для двумерной |
модели |
решетки они определяются проекцией линии уровня для поверхности E = E(kx , k) , эта линия представляет собой замкнутую кривую в пространстве импульсов (kx , ky ),
имеющую симметрию, соответствующую симметрии обратной решетки (т.е. зоны Бриллюэна). В трехмерном случае состояния с заданным
17
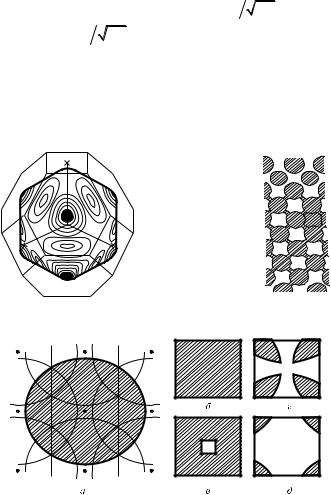
значением энергии образуют изоэнергетические поверхности в пространстве (рис. 1.13).
Наибольшую роль играют поверхности с энергией, равной энергии Ферми EF – поверхности Ферми (рис. 1.14, 1.15, электроны с
E = EF определяют многие макроскопические свойства кристал-
лов). Для свободной |
частицы |
(E = k 2 2m) |
эти сферы |
k 2 = kx2 +ky2 +kz2 = EF |
2m =const , |
для частицы в |
кристалличе- |
ской решетке такие сферы искажаются в большей или меньшей степени (см. рис. 1.14, в основном за счет того, что границы зон Бриллюэна пересекаются изоэнергетическими поверхностями под прямыми углами). Сложный вид приобретают изоэнергетические поверхности, выходящие за пределы первой зоны Бриллюэна, после их приведения к первой зоне (рис. 1.16).
Рис. 1.14. Поверхность Ферми |
Рис. 1.15. Сечение |
и границы зоны Бриллюэна для меди |
поверхности Ферми |
Рис. 1.16. Приведение сферы к первой зоне Бриллюэна: а – сфера в представлении повторяющихся зон; б – д – приведение к первой зоне от второй, третьей и четвертой зон Бриллюэна соответственно
18
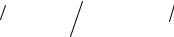
Так, поверхность Ферми алюминия в представлении расширенных зон близка к сферической. Эта поверхность, однако, захватывает четыре зоны Бриллюэна и после отображения в первую зону образует составленную из отдельных изолированных участков многосвязную сложную поверхность.
Плотность состояний
В пространстве импульсов (которому соответствует k-прост- ранство в представлении расширенных зон) число состояний определяется волновыми свойствами электрона, приводящими к конечному размеру электрона в k-пространстве: число состояний –
удвоенное число элементарных объемов =3. Для двумерной системы
dζ = (2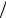 h2 )dpxdpy = 2
h2 )dpxdpy = 2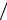 (2π)2 dkxdky
(2π)2 dkxdky
(фактор 2 учитывает два направления спина). Таким образом, плотность состояний равномерно распределена по k-пространству. Для нахождения распределения частиц по энергии
dN 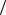 dE = f (E )d ζ
dE = f (E )d ζ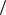 dE
dE
при известной функции распределения f(E) необходима плотность распределения не по импульсам, а по энергии g (E)= d ζ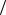 dE :
dE :
|
|
|
∫ |
|
g (E)dE = (d ζ |
dE)dE = 2 |
(2π)3 |
1 ( k E (k))dF (E)dE dE , |
|
|
|
|
(E=const) |
|
|
|
|
|
где k E – градиент в трехмерном k-пространстве; F(E) – площадь
изоэнергетической поверхности.
Такое интегрирование проводится для каждой энергетической полосы; там, где полосы перекрываются (т.е. одной энергии соответствуют разные значения k), плотности состояний складываются (рис. 1.17). Для энергий из «запрещенных зон», которым не соответствует ни одно разрешенное состояние, плотность состояний обращается в нуль (рис. 1.18).
19
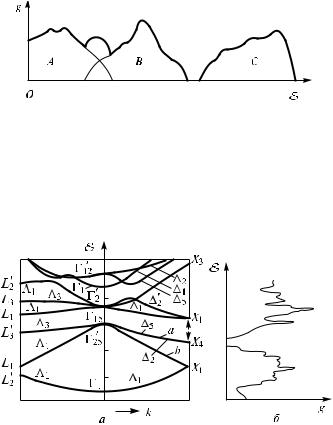
Рис. 1.17. К определению g(E) по дисперсионной зависимости
В пределах каждой зоны Бриллюэна в каждой ветви дисперсионной зависимости имеется 2N состояний (где N – число атомов в теле), причем очевидна нормировка g:
E∫2 gdE = 2N.
E1
Рис. 1.18. Дисперсионное соотношение для Si (а) и соответствующая ему зависимость плотности состояний от энергии (б)
Если вблизи границы зоны эффективную массу т* считать постоянной (функция E = E(k) близка к параболе), то плотность со-
стояний такая же, как и у свободных частиц, но с массой, равной т*:
g = (4π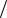 h3 )(2m* )3
h3 )(2m* )3 2 Ek1
2 Ek1 2 ,
2 ,
где |
Ek – кинетическая энергия, Ek = p / (2m* ); |
для электронов у |
|
дна |
зоны |
с эффективной массой те полная |
энергия E = E1 + |
+ р/(2те), |
для дырок вблизи верха зоны проводимости (с массой |
||
т*) |
|
|
|
|
|
20 |
|
