Кудряшов Методы нелинейной математич 2008

Задача Коши для этого уравнения в общем случае не решается. Уравненне не проходит тест Пенлеве на интегрируемость. Небольшой набор точных решений для этого уравнения получен в работах [126, 142].

1.15.Уравнение пятого порядка для описания волн под ледяным покровом

При описании волновых процессов на поверхности жидкости покрытой упругой пластиной (например, волны в океане под ледяным покровом) уже более двадцати лет используется уравнение

Уравнение (1.15.1) имеет два дисперсионных слагаемых, но не относится к классу точно решаемых, хотя имеет решение в виде уединенной волны [8, 29, 45]. Численное моделирование волновых процессов, описываемых уравнением (1.15.1), впервые проводилось Кавахарой [110]. Математические модели, описываемые уравнением (1.15.1), в настоящее время хорошо изучены [8, 29].

1.16.Нелинейное уравнение шестого порядка для описания процессов турбулентности

В последние годы при описании процессов турбулентности используется уравнение шестого порядка, содержащее слагаемые, учитывающие диссипацию и подкачку энергии в систему:

Уравнение (1.16.1) рассматривалось в работе [43] как пример уравнения шестого порядка, имеющего точные решения. При изучении физических процессов уравнение (1.16.1) появилось в работах [84, 137] как уравнение, которое описывает новый тип турбулентности.

Умножив все слагаемые уравнения (1.16.1) на u(x, t) и проинтегрировав по x от −∞ до ∞, получаем уравнение

Из уравнения (1.16.2) следует, что при α < 0, β < 0 и δ < 0 третий и пятый члены в уравнении (1.16.1) характеризуют процесс добавления энергии в систему, тогда как четвертый член отвечает за диссипативные процессы. В случае α > 0, β > 0 и δ > 0 роль слагаемых меняется: третий и пятый члены характеризуют диссипацию энергии в системе, описываемой уравнением, а четвертый член отвечает за подкачку энергии в систему. В зависимости от знаков коэффициентов α, β и δ возможны и другие варианты развития процессов.

Формально уравнение (1.16.1) обобщает уравнение Курамото—Сивашинского и по физической сути моделирует аналогичные процессы. Строгий вывод уравнения (1.16.1) в настоящее время отсутствует. Уравнение (1.16.1), как и уравнение Курамото—Сивашинского, не относится к классу точно решаемых уравнений, не имеет решений в виде солитонов, но имеет некоторый набор частных решений при некоторых соотношениях между параметрами уравнения. Численное моделирование

ut + α u ux = D uxx + β u + γ u2 − δ u3, D = 0. (1.18.1)

В уравнении (1.18.1) предполагается, что D — коэффициент диффузии, α характеризует нелинейный перенос популяции, а параметры β, γ и δ описывают нелинейный источник.

Пусть в среде происходит размножение какого-либо вида организмов.Тогда динамика системы при учете смертности и диффузионного перемещения популяции по среде описывается уравнением

где n — численность популяции в расчете на единицу объема, m(n) — масса пищи, k — коэффициент убыли и κ — коэффициент прироста популяции [55]. Если считать, что масса пищи меняется по закону m(n) = m0(1 − n/n0), то уравнение (1.18.2) будет уравнением Бюргерса—Хаксли c α = 0.

Кроме описания динамики популяций, уравнение (1.18.1) встречается и при описании ряда других нелинейных волновых явлений. Например, уравнение

описывающее движение доменной стенки сегнетоэлектрика в электрическом поле, при α = 0 сводится к уравнению (1.18.1) с помощью линейной замены. В уравнении (1.18.3) P — дипольный момент, E — внешнее электрическое поле. Левая часть характеризует диссипативный процесс перехода электростатической энергии в тепловую, τ — характерное время релаксации дипольного момента. Первое слагаемое в правой части уравнения описывает взаимодействие между дипольными моментами соседних областей сегнетоэлектрика, остальные слагаемые определяют величину дипольного момента в однородном сегнетоэлектрике [23].

Установлено, что уравнение (1.18.1) не проходит теста Пенлеве [39] и, следовательно, в общем случае не является точно решаемым уравнением.

Для описания динамики популяций в периодической литературе встречается также обобщенное уравнение Бюргерса—

Уравнение (1.18.4) не относится к классу точно решаемых уравнений и не проходит тест Пенлеве, однако имеет небольшой набор точных решений. Математическая модель, описываемая уравнением (1.18.4), в настоящее время изучена не достаточно подробно.

1.19.Уравнения фильтрации газа в пористой среде

Одномерное движение газа в пористой среде можно описать системой уравнений газовой динамики с учетом сил трения, возникающих при взаимодействии газа с твердой средой [40]:

где ε — пористость среды, ρ — плотность газа, u — массовая скорость, P — давление газа, x — координата, F (u) — сила сопротивления, ν — индекс симметрии, (ν = 0 соответствует случаю плоской фильтрации, при ν = 1 — цилиндрически симметричное движение газа, в случае ν = 2 — сферически симметричное движение).

Система уравнений (1.19.1) дополняется уравнением состояния, связывающим давление и плотность газа. Обычно в качестве такого уравнения используется уравнение состояния политропического газа

Предполагая справедливость закона Дарси и учитывая зависимость давления газа от плотности в форме политропы, из уравнения (1.19.1) имеем:

В случае зависимости градиента давления от квадрата скорости для изотермической фильтрации газа имеем

где c0 — изотермическая скорость звука. В этом случае при ν = 0 из закона сохранения массы (1.19.1) получаем уравнение для скорости движения в виде:

Это уравнение совпадает с уравнением Бюргерса, в котором вязкость обратно пропорциональна скорости фильтрации газа.

1.20.Нелинейное уравнение теплопроводности

Уравнение (1.19.7) совпадает с уравнением нелинейной теплопроводности если воспользоваться заменой ρ(x, t) → T (x, t) [27].

Нелинейное уравнение теплопроводности часто записывается с учетом нелинейного источника

где f (T ) — зависимость источника от температуры. Подобные математические модели рассматриваются при изучении многочисленных задач физики горения [28].

При f (T ) = 0 уравнение (1.20.1) является нелинейным уравнением теплопроводности, обобщающим хорошо известное линейное уравнение теплопроводности на случай учета зависимости коэффициента теплопроводности от температуры в виде степенной функции. Это уравнение описывает процессы распространения тепла при высоких температурах, когда за механизм переноса тепла ответсвенны электронная или лучистая теплопроводность.

Известны автомодельные решения ряда задач, описываемых уравнением (1.20.1) при f (T ) = 0. Впервые аналитеское решение задачи при наличии мгновенного точечного источника получили Я.Б. Зельдович и А.С. Компанеец [26]. Приближенные решения краевых задач на полубесконечной прямой получены в работах [40, 47, 51].

В случае f (T ) = 0 уравнение (1.20.1) стало популярным в связи с изучением режима с обострением температуры, исследование которого проводилось А.А. Самарским, С.П. Курдюмовым и их учениками. Детальное исследование многих задач нелинейной теплопроводности можно найти в монографиях [5, 15, 65].

1.21.Модель Хенона—Хейлеса

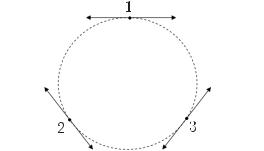
Модель Хенона и Хейлеса впервые появилась при численном исследовании движения звезды в среднем поле галактики [55]. Система уравнений, описывающая это движение, может быть получена при рассмотрении взаимодействия трех одинаковых масс, расположенных в вершинах равностороннего треугольника [39, 53, 55].

Пусть имеются три взаимодействующие массы, как показано на рис. 1.8. Система уравнений для описания движения каждой из масс имеет вид

Рис. 1.8. Взаимодействие трех масс в модели Хенона—Хейлеса

80 Глава 1. Нелинейные математические модели

Это два первых интеграла. Выражение для третьего интеграла, имеющего вид

поненты в (1.21.8), при малых x и y получаем гамильтониан Хенона—Хейлеса