
Кудряшов Методы нелинейной математич 2008
.pdfПредисловие |
11 |
гих выдающихся ученых. В настоящее время такие методы носят название методов Пенлеве и являются предметом изучения аналитической теории дифференциальных уравнений.
Как нередко бывает в науке, направление, о котором пойдет речь в книге, прошло все этапы своего развития, от этапа бурного развития, последующего за ним этапа забвения, до этапа возрождения, когда многие подходы и методы были открыты вновь. Однако главным является то обстоятельство, что в настоящее время методы Пенлеве стали мощным инструментом решения задач и с их помощью даны ответы на многие вопросы теории дифференциальных уравнений.
Для демонстрации методов, предложенных в книге, выбраны наиболее популярные нелинейные дифференциальные уравнения и знаменитые системы уравнений: система Лоренца и система Хенона—Хейлеса. Книгу можно рассматривать как справочник по наиболее известным нелинейным дифференциальным уравнениям и методам их решения. В ней дается краткая история открытия известных нелинейных дифференциальных уравнений и предлагается информация о физических процессах, при описании которых эти уравнения встречаются. Отличительной особенностью книги является тот факт, что основное внимание в ней уделено построению точных решений нелинейных дифференциальных уравнений. Еще одна отличительная черта книги — для успешного и эффективного применения представленных в ней методов следует использовать математические пакеты вычислений типа MAPLE и MATHEMATICA.
Уравнения, которые рассматриваются в данной книге, условно можно разделить на два класса. К первому классу относятся нелинейные уравнения в частных производных, для которых может быть решена задача Коши при начальном условии достаточно общего вида. О таких уравнениях будем говорить как о точно решаемых нелинейных уравнениях. В зарубежной литературе, а в последнее время и в русскоязычной об уравнениях этого типа говорят как об интегрируемых уравнениях. Для наи-
12 |
Предисловие |
более популярных нелинейных уравнений математической физики — Кортевега—де Вриза, нелинейного уравнения Шредингера и sin-Гордона — можно сказать, что они являются и точно решаемыми, и интегрируемыми нелинейными дифференциальными уравнениями. Точно решаемых нелинейных уравнений в частных производных в настоящее время известно достаточно много. Строго говоря, их бесконечно много, если принять во внимание тот факт, что каждому интегрируемому уравнению соответствует целая иерархия уравнений.
Второй класс уравнений условно можно назвать классом частично интегрируемых уравнений. Задача Коши для них в общем случае не решается. При поиске точных решений уравнений указанного класса обычно используются автомодельные переменные или переменные бегущей волны. Задача Коши для таких уравнений может быть решена только для конкретного, как правило, заранее неизвестного начального условия.
Предлагаемая читателю книга состоит из пяти разделов. В первом приводятся наиболее популярные нелинейные дифференциальные уравнения (уравнение Кортевега—де Вриза, нелинейное уравнение Шредингера, уравнение sin-Гордона, уравнение Бюргерса, уравнение Курамото—Сивашинского и др.) и известные нелинейные системы дифференциальных уравнений. Предлагаются выводы некоторых уравнений и дается информация о физических процессах, при описании которых встречаются обсуждаемые дифференциальные уравнения.
Во втором разделе обсуждаются элементы группового анализа дифференциальных уравнений. Применение методов теории группового анализа в настоящее время детально изложено в целом ряде книг (см., например, монографии [30, 61, 62]). Этот раздел в данной книге имеет вспомогательный характер, поскольку решения нелинейных дифференциальных уравнений в частных производных часто находятся путем перехода к обыкновенным дифференциальным уравнениям, используя инвариантные переменные, полученные с помощью групп преобразований.
Предисловие |
13 |
Втретьем разделе книги содержатся сведения, которые можно классифицировать как аналитические свойства нелинейных дифференциальных уравнений. В этом разделе описаны наиболее общепринятые в настоящее время алгоритмы анализа обыкновенных дифференциальных уравнений на свойство Пенлеве и обсуждается связь нелинейных уравнений в частных производных
сОДУ, имеющими свойство Пенлеве. Предложены пары Лакса для уравнения Кортевега—де Вриза, позволяющие решить задачу Коши для этого уравнения. Даются выводы преобразований Бэклунда для второго уравнения Пенлеве, для уравнения sin-Гордона и для уравнения Кортевега—де Вриза.
Вчетвертом разделе предложены методы решения, применимые для широко известных нелинейных уравнений в частных производных: для уравнения Кортевега—де Вриза, модифицированного уравнения Кортевега—де Вриза, нелинейного уравнения Шредингера и уравнению sin-Гордона. Задача Коши для перечисленных уравнений решается методом обратной задачи рассеяния, но их простейшие решения находятся с помощью перехода к обыкновенным дифференциальным уравнениям, используя переменные бегущей волны.
Вэтом разделе обсуждается также метод обратной задачи рассеяния решения задачи Коши для уравнений Кортевега—де Вриза и sin-Гордона. Для уравнения Кортевега—де Вриза рассмотрен метод Хироты, с помощью которого находятся солитонные решения точно решаемых нелинейных уравнений в частных производных. Часть материала, относящаяся к методу обратной задачи рассеяния решения задачи Коши для уравнений Кортевега—де Вриза и sin-Гордона, изложена конспективно. Указанный метод в настоящее время детально изложен в недавно изданной книге автора: Кудряшов Н.А. Аналитическая теория нелинейных дифференциальных уравнений. М.-Ижевск: Институт компьютерных исследований, 2004.
Впятом разделе содержится ряд методов, которые применяются при построении точных решений нелинейных дифференци-
14 |
Предисловие |
альных уравнений. Методы, предлагаемые в этом разделе, могут использоваться и при нахождении точных решений интегрируемых уравнений, но наиболее эффетивны они при поиске решений уравнений, для которых задача Коши в общем случае не решается. Процедура построения решений обычно содержит этап перехода к обыкновенным дифференциальным уравнениям, и методы по существу применяются для построения решений нелинейных обыкновенных дифференциальных уравнений.
Автор надеется, что книга будет полезна студентам и аспирантам, научным сотрудникам и преподавателям, интересующимся построением нелинейных математических моделей и методами нахождения аналитических решений нелинейных дифференциальных уравнений.
Предлагаемая книга написана на основе курса лекций, читаемого автором более двадцати лет студентам четвертого и пятого курсов кафедры Прикладная математика Московского инженерно-физического института (государственного университета). Вопросы затронутые в книге неоднократно обсуждались на научных семинарах с коллегами по кафедре, а также на конференциях, посвященных изучению нелинейных эволюционных уравнений и динамических систем. Особенно полезны были дискуссии с профессорами А.В. Аксеновым, В.И. Громаком, М. Крускалом, Р. Контом, Э. Пикерингом и В.И. Цигельником. Всем им автор выражает свою искреннюю признательность.
При подготовке рукописи к печати оказали большую помощь Н.Б. Логинова и М.А. Чмыхов, которым автор выражает благодарность.
Глава 1
Нелинейные математические модели
1.1.Уравнение Кортевега—де Вриза для описания волн на воде
Явление распространения волн на поверхности воды издавна привлекало к себе внимание исследователей. Это — пример волн, которые каждый мог наблюдать еще в детстве и которые обычно демонстрируются в рамках школьного курса физики. Однако это довольно сложный тип волн. По выражению Ричарда Фейнмана, «более неудачного примера для демонстрации волн придумать трудно, ибо эти волны нисколько не похожи ни на звук, ни на свет; здесь собрались все трудности, которые могут быть в волнах» [69].
Если рассмотреть бассейн, наполненный водой, и на его поверхности создать некоторое возмущение, то по поверхности воды начнут распространяться волны. Возникновение их объясняется тем, что частицы жидкости, которые находятся вблизи впадины, при создании возмущения будут стремиться заполнить впадину,
16 |
Глава 1. Нелинейные математические модели |
находясь под действием силы тяжести. Эволюция этого явления с течением времени и приведет к распространению волны на воде. Частицы жидкости в такой волне двигаются не вверх-вниз, а приблизительно по окружностям, поэтому волны на воде не являются ни продольными, ни поперечными. Они как бы являются смесью тех и других. С глубиной радиусы окружностей, по которым двигаются частицы жидкости, уменьшаются до тех пор, пока не станут равными нулю [70].
Если анализировать скорость распространения волны на воде, то оказывается, что эта скорость зависит от ее амплитуды. Скорость длинных волн пропорциональна корню квадратному из ускорения свободного падения, умноженному на сумму амплитуды волны и глубины бассейна. Причиной возникновения таких волн является сила тяжести.
Для коротких волн возникновение восстанавливающей силы обусловлено силой поверхностного натяжения, и потому скорость таких волн пропорциональна корню квадратному из частного, в числителе которого стоит поверхностное натяжение, а в знаменателе — произведение длины волны на плотность воды. Для волн средней длины скорость их распространения зависит от всех перечисленных выше параметров задачи. Из сказанного ясно, что волны на воде и в самом деле явление довольно сложное.
Любопытную волну на воде наблюдал шотландский ученый Джон Скотт Рассел в 1834 г. Рассел занимался изучением пропускной способности канала Юнион, который начинается у Эдинбурга и соединяет через канал Форз — Клайд два берега Шотландии. Обратимся к замечательному описанию этого наблюдения самим Расселом [66].
«Я следил за движением баржи, которую быстро тянула по узкому каналу пара лошадей, когда баржа неожиданно остановилась; но масса воды, которую баржа привела в движение, не остановилась; вместо этого она собралась около носа судна в состоянии бешеного движения, затем неожиданно оставила его позади, катясь вперед с огромной скоростью и принимая форму большого

1.1. Уравнение Кортевега—де Вриза |
17 |
одиночного возвышения, т.е. округлого, гладкого и четко выраженного водяного холма, который продолжал свой путь вдоль канала, нисколько не меняя своей формы и не снижая скорости. Я поскакал за ним верхом, и, когда я нагнал его, он по-прежнему катился вперед со скоростью приблизительно восемь или девять миль в час, сохранив свой первоначальный профиль возвышения длиной около тридцати футов и высотой от фута до фута с половиной. Его высота постепенно уменьшалась, и после одной или двух миль погони я потерял его в изгибах канала. Так в августе 1834 года мне впервые довелось столкнуться с необычайным и красивым явлением, которое я назвал волной трансляции; теперь это название общепринято».
Джон Рассел на протяжении всей своей жизни неоднократно возвращался к наблюдению за уединенной волной. Он верил, что открытая им волна играет очень важную роль во многих явлениях в природе. Им были установлены некоторые свойства этой волны. Во-первых, он заметил, что она движется с постоянной скоростью и без изменения формы. Во-вторых, он нашел зависимость скорости этой волны от глубины канала h и высоты волны a:
C = g (a + h),
где g — ускорение свободного падения; причем a < h. В-третьих, Рассел обнаружил, что возможен распад одной большой волны на несколько волн. В-четвертых, он отмечал, что в экспериментах наблюдаются только волны возвышения. Известно также, что он заметил, что открытые им уединенные волны проходят друг через друга без каких-либо изменений, но на последнее очень важное свойство он не обратил серьезного внимания.
Работа Рассела, которая была опубликована им в 1844 году как «Доклад о волнах» [143], вызвала осторожную реакцию в среде ученых. В европейских странах работу не заметили, но в самой Англии на нее обратили внимание Эйри и Стокс. Эйри
18 |
Глава 1. Нелинейные математические модели |
подверг критике результаты экспериментов, которые наблюдал Рассел, и отметил, что из теории длинных волн на мелкой воде выводы Рассела не получаются, а также утверждал, что длинные волны не могут сохранять неизменной формы. Эйри не поверил наблюдениям Рассела.
Один из основателей современной гидродинамики — Джордж Габриэль Стокс также не согласился с результатами наблюдений уединенной волны, полученными Расселом, и критически отнесся к факту существования уединенных волн.
После столь негативного отношения к уединенной волне долгое время о ней никто не вспоминал, кроме самого Рассела. Даже приближаясь к старости он писал: «Это самое прекрасное и необычайное явление; день, когда я впервые увидел его, был лучшим днем моей жизни. Никому никогда не посчастливилось наблюдать его раньше или, во всяком случае, понять, что оно значит. Теперь оно известно как уединенная волна трансляции. Никто прежде и вообразить не мог, что уединенная волна возможна. Когда я описал ее сэру Джону Гершелю, он сказал: «Это просто вырезанная половина обычной волны». Но это не так, поскольку обычные волны идут отчасти ниже поверхности воды; кроме того, ее форма совсем иная. Это не половина волны, а несомненно вся волна целиком, с тем отличием, что волна как целое не находится попеременно то ниже, то выше поверхности, а всегда выше ее. Этого вполне достаточно, чтобы такой холм воды не стоял на месте, а двигался».
Определенную ясность в результаты наблюдений Рассела внесли Буссинеск (1872 год) и Рэлей (1876 год), которые независимо друг от друга получили формулу, описывающую характер возвышения свободной поверхности на воде в виде квадрата гиперболического секанса, и вычислили скорость распространения уединенной волны на воде.
Позже опыты Рассела были повторены другими исследователями, которые подтвердили его результаты.
Окончательная ясность в проблеме, возникшей после опытов
1.1. Уравнение Кортевега—де Вриза |
19 |
Джона Рассела по изучению уединенной волны, наступила только после появления работы датских ученых Кортевега и де Вриза, которые попытались разобраться в существе дела. Эти ученые, обобщив метод Рэлея, вывели в 1895 году уравнение для описания одноволнового приближения при распространении волн на воде.
Следуя их работе, рассмотрим процесс распространения малых, но конечных возмущений на поверхности жидкости. О таких возмущениях обычно говорят как о гравитационных волнах, подчеркивая тем самым, что ответственными за возникновение и распространение этих волн являются гравитационные силы.
Предположим, что плотность жидкости при возмущениях поверхности не меняется (ρ0 = const), тогда уравнение непрерывности запишется [54]
|
|
|
→ |
|
(1.1.1) |
|
|
|
div u = 0. |
||
Уравнение движения в поле сил тяжести можно представить |
|||||
в виде: |
|
|
|
|
|
|
→ |
+ |
→u , →u + ρ0 |
P = −g →j , |
(1.1.2) |
|
∂t |
||||
|
∂ u |
|
1 |
|
|
→
где j — единичный вектор в направлении силы тяжести.
Как правило, при распространении возмущений движение жидкости можно считать безвихревым, поскольку типичные задачи, возникающие в теории волн, рассматриваются при первоначально покоящейся жидкости или в однородном потоке. Извест-
|
|
|
→ |
→ |
но, что если в начальный момент времени вихрь ω = rot u = 0, |
||||
|
|
→ |
[52]. |
|
то и в последующие моменты времени ω = 0 |
|
|||
Если ввести потенциал скорости ϕ, определенный выражени- |
||||
ем |
|
|
|
|
→ |
= grad |
ϕ |
|
(1.1.3) |
u |
|
|||
|
, |
|
||
20 |
Глава 1. Нелинейные математические модели |
то уравнение (1.1.1) перейдет в уравнение Лапласа:
ϕ = 0. |
(1.1.4) |
Пользуясь формулой векторного анализа
→− |
× rot→− →− |
|
→− |
2 |
→− |
|
|
|
u |
( u ) + ( u , |
|
) u = |
1 |
|
u |
2 |
, |
|
|
|
|
|||||
уравнение (1.1.2) для безвихревого движения можно привести к виду
→ |
1 |
|
|
|
|
|
|
|
→ |
|
|
∂ u |
|
|
2 |
|
|
|
P |
|
|||
|
+ |
|
|
u |
|
|
+ |
|
+ g j = 0, |
|
|
|
2 |
|
|
ρ0 |
(1.1.5) |
||||||
∂t |
|
|
|
|
|||||||
откуда после интегрирования по z с учетом (1.1.3) получаем
∂ϕ |
+ |
1 |
( ϕ)2 |
+ |
P − P0 |
+ gz = 0. |
(1.1.6) |
|
2 |
|
|||||
∂t |
|
|
|
ρ0 |
|||
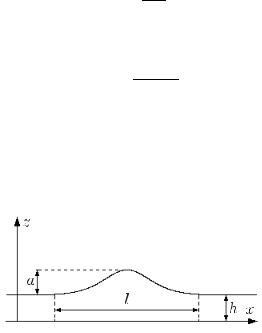
В формуле (1.1.6) принято, что ось z направлена вертикально вверх против ускорения свободного падения (рис. 1.1), зависимость от времени, полученная при интегрировании уравнения (1.1.5) по z, включена в потенциал, P0 — давление окружающей атмосферы на поверхность жидкости.
Рис. 1.1. Характеристики плоского возмущения на поверхности жидкости, используемые при выводе уравнения Кортевега—де Вриза
