
Кудряшов Методы нелинейной математич 2008
.pdf
1.10. Уравнение sin-Гордона |
51 |
аций, могут появиться точечные дефекты иного происхождения. В частности, один из методов увеличения количества дефектов состоит в бомбардировке твердого тела атомами или частицами с высокой энергией путем нейтронного облучения в ядерном реакторе. В результате облучения быстрые частицы соударяются с атомами решетки и смещают их, образуя при этом также дефекты по Френкелю.
Пусть имеется простейшая кристаллическая структура, состоящая из слоев атомов, расположенных на некотором расстоянии друг от друга. Рассмотрим математическую модель поведения точечного дефекта в кристаллической структуре твердого тела, предложенную Я.И. Френкелем и Т.А. Конторовой в 1926 году [71]. Дефекты, рассматриваемые в модели Френкеля и Конторовой, иногда называются дислокациями, однако заметим, что в настоящее время под дислокацией понимается более сложное несовершенство кристаллической структуры, чем любой из точечных дефектов [74].
Предположим, что атомы в кристаллической структуре движутся по прямой вдоль оси x, направленной перпендикулярно атомным слоям, и, следовательно, все силы, действующие на атомы также направлены вдоль оси x. Влияние соседних атомных слоев на отдельный атом можно описать периодическим потенциалом [74]
2πx
V (x) = A 1 − b cos , b < 1 (1.10.1) a
где x — координата, a — шаг кристаллической решетки, A и b — постоянные, характеризующие потенциал. Обозначая отклонение n-го атома от положения равновесия в виде
yn(t) = xn(t) − na, |
(1.10.2) |
где xn(t) — координата n-го атома, находим, что на n-й атом со стороны атомных слоев действует сила

52 |
Глава 1. Нелинейные математические модели |
|
|||||
|
|
2 |
πAb |
sin |
2πy |
. |
|
|
f (yn) = − |
|
n |
(1.10.3) |
|||
|
|
a |
a |
||||
Возможным случаем дислокации в твердом теле является дырка, которая перемещается в нем из-за перескока атомов.
Если в кристаллической структуре дефект отсутствует, то равновесная конфигурация в модели соответствует такому состоянию, что в каждой впадине потенциала (1.10.1) находится один атом. Однако в случае положительной (или отрицательной) дислокации, когда число частиц меньше (или больше) их первоначального количества, равновесная конфигурация нарушается и возникает новая, аналог которой представлен на рис. 1.5.
Рис. 1.5. Возникновение дислокации в модели Френкеля—Конторовой при удалении одного из атомов в кристаллической структуре
Соседние атомы, находящиеся в равновесной конфигурации, при дислокации также взаимодействуют друг с другом. На рис. 1.5 такое взаимодействие иллюстрируется пружинками, а крестиками изображено положение атомных слоев.
Аналогом предложенной Френкелем и Конторовой модели дислокаций является периодическая последовательность ложбинок и горок, которые представлены на рис. 1.5. В равновесной конфигурации во всех ложбинках лежат шарики, которые соединены пружинками. Если один из шариков вместе с пружинкой удаляется (или, наоборот, один из шариков вместе с пружинкой добавляется), то равновесная конфигурация нарушается, и си-

1.10. Уравнение sin-Гордона |
53 |
стема, соединенная пружинками, придет в движение. Из-за связи между собой шарики сместятся и уже не будут находиться строго в ложбинках.
Уравнение движения n-го атома с учетом потенциала (1.10.1) и в предположении, что пружинки действуют на n-й атом с силой, пропорциональной разности отклонений от положения равновесия, запишется в виде
myn,tt = − |
2πAb |
sin |
2πyn |
+ |
k |
(yn+1 − 2yn + yn−1) , |
(1.10.4) |
a |
a |
h2 |
где m — масса частицы, k — коэффициент пропорциональности в силе, действующей между соседними атомами, h — расстояние между атомами.
Переходя в (1.10.4) к непрерывно распределенным массам при условии, что расстояние между атомами стремится к нулю, а их число — к бесконечности, получаем уравнение
myn,tt = − |
2πAb |
sin |
2πyn |
+ k (yn)xx . |
(1.10.5) |
a |
a |
Введем обозначения
ϕ = |
2πyn |
, |
t = |
2π |
|
Ab |
· t, |
x = |
2π |
|
Ab |
x |
(1.10.6) |
a |
a |
|
m |
a |
|
k |
(далее штрихи опускаем), тогда (1.10.5) приводится к виду
ϕtt − ϕxx + sin ϕ = 0. |
(1.10.7) |
Это уравнение носит название уравнения sin-Гордона. Название звучит несколько странно, но оно связано с тем, что при малых значениях ϕ уравнение (1.10.7) переходит в уравнение Клейна—Гордона
54 |
Глава 1. Нелинейные математические модели |
ϕtt − ϕxx + ϕ = 0.
Подобное укороченное название, придуманное Мартином Крускалом, как раз и породило название sin-Гордона для уравнения (1.10.7).
Заметим, что если использовать в уравнении (1.10.7) замену переменных
x = ξ + τ t = τ − ξ,
то уравнение sin-Гордона примет вид
uξτ = sin u. |
(1.10.8) |
Такая запись уравнения sin-Гордона является также широко распространенной.
Уравнение (1.10.7) так же, как и выше приведенные уравнения Кортевега—де Вриза и нелинейное уравнение Шредингера, широко используются при описании многих явлений в физике.
Впервые это уравнение появилось в дифференциальной геометрии как точная модель описания поверхности постоянной отрицательной кривизны. Изучению этого вопроса была посвящена работа А. Бэклунда в 1980 году, в которой показано, что первая фундаментальная квадратичная форма при постоянной отрицательной кривизне преобразуется к уравнению sin-Гордона [1, 75].
Это уравнение используется также при анализе свойств элементарных частиц и при теоретическом описании эффекта самоиндуцированной прозрачности. Этот удивительный эффект был открыт в работе Маккола и Хана в 1965 году при изучении процесса распространения ультракоротких импульсов электромагнитного излучения в рубиновом стержне [1, 57, 59, 138]. Самоиндуцированная прозрачность возникает при взаимодействии электромагнитного излучения с диэлектриком на частоте, близкой к
1.11. Нелинейное уравнение переноса |
55 |
резонансной. Самый простой случай возникновения эффекта реализуется для диэлектрика, состоящего из двухуровневых атомов, каждый из которых имеет основное и возбужденное состояние. Если в начальный момент атомы находятся в основном состоянии, то под действием электромагнитного излучения они переходят в возбужденное состояние, поглощая энергию ультракоротких импульсов и возвращая ее полностью обратно при вынужденном переходе в исходное состояние [57, 138]. При этом, взаимодействуя с импульсом электромагнитного излучения, атомы вещества остаются в основном состоянии, и суммарной передачи энергии от излучения к веществу не происходит. Импульс распро-
страняется в среде, которая для него становится прозрачной, что и послужило поводом назвать этот эффект самоиндуцированной прозрачностью.
1.11.Нелинейное уравнение переноса и уравнение Бюргерса
Одним из самых простых по внешнему виду уравнений является нелинейное уравнение переноса [39, 64]
ut + uux = 0. |
(1.11.1) |
Уравнение (1.11.1) имеет нелинейное слагаемое, аналогичное слагаемому в уравнении Кортевега—де Вриза.
Решение задачи Коши для уравнения (1.11.1) в настоящее время хорошо известно. Это решение обладает рядом свойств, не характерных для линейных уравнений [4, 64].
Пусть в начальный момент времени задано начальное возмущение
56 |
Глава 1. Нелинейные математические модели |
u(x, t = 0) = ψ (x) . |
(1.11.2) |
Решение уравнения (1.11.1) с условием (1.11.2) находится методом характеристик. Предположим, что решение задачи является гладкой функцией. Пусть x = ϕ (t) определяется из уравнения
dx |
= u (x, t = 0) . |
(1.11.3) |
|
dt |
|||
|
|
Эти линии являются характеристиками уравнения (1.11.1). Решение вдоль каждой характеристики может зависеть от t, по-
этому получаем |
|
|
|
|
|
|
|
|
|
|
du |
= |
∂u |
+ |
dx |
|
∂u |
= 0. |
(1.11.4) |
|
dt |
∂t |
|
|
|||||
|
|
|
dt ∂x |
|
|||||
Вдоль характеристики решение постоянно. В силу (1.11.3) ха- |
|||||||||
рактеристики являются прямыми линиями |
|
||||||||
|
|
x = ψ (x0) t + x0, |
(1.11.5) |
||||||
где x0 — абсцисса точки, из которой выпускается характеристика; ψ (x0) — коэффициент, характеризующий наклон прямой к оси ординат. Таким образом, начальное условие (1.11.2) задает картину характеристик и значения решения в каждой точке плоскости (x, t). При монотонном возрастании функции ψ (x0) с ростом x0 угол наклона фукции к оси ординат увеличивается, а характеристики не пересекаются. Однако для убывающей функции с ростом x0 характеристики будут пересекаться в некоторый момент времени. Возникает вопрос о выборе однозначного решения при пересечении характеристик. Этот выбор можно сделать, принимая во внимание закон сохранения для уравнения (1.11.1). Заметим, что это уравнение можно представить в виде:
∂u |
|
1 |
|
∂u2 |
|
|
|
+ |
|
|
|
= 0. |
(1.11.6) |
∂t |
2 |
∂x |
||||
1.11. Нелинейное уравнение переноса |
57 |
||
Дифференцируемые решения уравнений (1.11.1) и (1.11.6) |
|||
удовлетворяют уравнению |
|
||
1 |
|
|
|
udx − |
|
u2dt = 0, |
(1.11.7) |
2 |
|||
G
где G — произвольный контур лежащий в полуплоскости t > 0. Пусть L — произвольный участок линии разрыва в контуре, тогда из (1.11.7) на этой линии получаем соотношение:
L |
1 |
|
|
|
|
|
||
[u] |
dx |
|
u2 |
|
dt = 0, |
(1.11.8) |
||
dt |
− |
2 |
|
|
||||
где [F ] обозначает скачок характеристики F на L: |
|
|||||||
[F ] = Fp − Fl. |
(1.11.9) |
|||||||
Поскольку L — произвольный участок линии разрыва, то из (1.11.8) имеем
|
|
|
dx |
1 |
|
|
|
|||
(up − ul) |
|
|
|
= |
|
up2 − ul2 |
, |
(1.11.10) |
||
dt |
2 |
|||||||||
откуда получаем условие на линии разрыва |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
1 |
|
|
|
|
|
|||
|
|
= |
|
(up + ul) . |
|
(1.11.11) |
||||
|
dt |
2 |
|
|||||||
Линия разрыва является границей, через которую характеристики не переносят своих значений, и это обстоятельство позволяет построить для уравнения (1.11.1) обобщенное решение задачи Коши, которое остается однозначным. Заметим, что для уравнения (1.11.1) можно записать бесконечное число законов сохранения, аналогичных (1.11.7), и может показаться, что выбор линии разрыва становится также неоднозначным. Однако при выборе закона сохранения необходимо принимать во внимание принцип сохранения физических величин. Учет именно такого закона позволяет сделать правильный выбор обобщенного решения.

58 |
Глава 1. Нелинейные математические модели |
Рис. 1.6. Начальное возмущение (1.11.12) для нелинейного уравнения переноса (1.11.1)
Рассмотрим решение уравнения (1.11.1) с начальным услови-
ем (рис. 1.6.) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
− |
1; |
|
|
|
2, |
|
|
|
|
||||
|
2 − |
|
|
− |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u (x, t = 0) = ψ(x) = |
|
|
(3 |
x), |
|
1 < x < 1; |
(1.11.12) |
||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1. |
|
|
|
1, |
|
|
|
|
|||||
Поскольку при x0 −1 |
|
|
|
|
|
|
|
|
|
ψ (x0) = 2, |
|
dx |
= 2, |
|
|
||||
|
dt |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
то получаем решение |
|
|
|
|
|
|
|
|
|
u (x, t) = 2, |
x 2t − 1. |
(1.11.13) |
|||||||
Принимая во внимание, что при x0 1 |
|
|
|||||||
ψ (x0) = 1, |
|
dx |
= 1, |
|
|
||||
|
dt |
|
|
||||||
|
|
|
|
|
|
|
|
|
|

|
|
1.11. Нелинейное уравнение переноса |
59 |
|||||||||||||||||||||
находим решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
u (x, t) = 1, |
|
|
1 + t x. |
(1.11.14) |
|||||||||||||||||
Для промежуточной области имеем |
|
|
|
|
|
|||||||||||||||||||
|
|
ψ (x0) = |
1 |
(3 − x0) , |
|
|
dx |
= |
1 |
(3 − x0) , |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
dt |
2 |
|
|||||||||||||||||
откуда получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
u (x, t) = |
3 − x |
, 2t |
− |
1 |
|
x |
|
1 + t. |
(1.11.15) |
|||||||||||||
|
|
2 |
− |
t |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В силу (1.11.11) линия разрыва определяется уравнением |
||||||||||||||||||||||||
|
|
|
|
x = |
|
3 |
t, |
|
t 2, |
|
|
|
x 3. |
(1.11.16) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
Окончательно получаем решение при x 3 в виде |
|
|||||||||||||||||||||||
|
|
|
3 |
|
|
x |
x |
|
2t |
− |
1; |
|
|
|
|
|
||||||||
|
|
|
2, |
|
|
t |
− |
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
u(x, t) = |
|
|
− |
|
, |
2t |
|
1 < x < t + 1; |
(1.11.17) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t + 1. |
|
|
|
|
|
|
|||||||||
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
При x |
|
3 решение определяется формулой |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||
|
|
|
|
|
u (x, t) = 2, x < |
2 t; |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
x > |
2 |
t. |
|
||||||
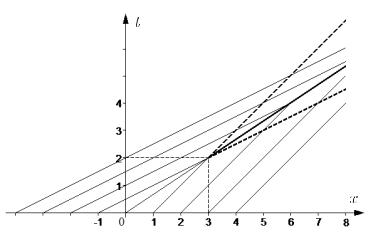
Полученное решение |
|
иллюстрируется на рис. 1.7. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Остановимся на обсуждении обобщения уравнения (1.11.1) в |
||||||||||||||||||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ut + αuux = μuxx. |
(1.11.18) |
||||||||||||||||
Уравнение (1.11.18) рассматривалось Дж. М. Бюргерсом [86] и носит название уравнения Бюргерса. Оно относится также к
60 |
Глава 1. Нелинейные математические модели |
Рис. 1.7. Решение задачи Коши, описываемой нелинейным уравнением переноса при начальном возмущении (1.11.12)
классу простейших уравнений и учитывает процесс нелинейного переноса и процессы диссипации, поскольку член с параметром μ отвечает за диссипацию возмущения u(x, t) в среде. Уравнение (1.11.18) возникает в газовой динамике, если в уравнении Эйлера учесть вязкие силы, и при описании концентрации вещества в среде, если скорость переноса линейно зависит от самой концентрации [55]. Полагая α = 0 в (1.11.18), имеем уравнение диффузии:
ut = μuxx. |
(1.11.19) |
Описание методов решения краевых задач и задач Коши для уравнения (1.11.19) можно найти во многих книгах по уравнениям математической физики [4, 63, 64, 65]. Особенный интерес к уравнению (1.11.18) возник в связи с открытием замечательного факта [91, 101], состоящего в том, что уравнение (1.11.18) с помощью преобразования Коула—Хопфа
