Кудряшов Методы нелинейной математич 2008

Из уравнения (4.5.14) следует, что f3 = 0, и поэтому в этом случае ряд (4.5.7) обрывается при n 3.

222 Глава 4. Методы решения интегрируемых уравнений

Принимая во внимание (4.5.7), (4.5.19) и (4.5.21), имеем

Подстановка (4.5.23) в формулу (4.5.1) приводит к двухсолитонному решению уравнения Кортевега—де Вриза. Это решение описывает процесс распространения и взаимодействия двух солитонов уравнения Кортевега—де Вриза.

Остановимся на обсуждении характера взаимодействия солитонов, описываемых формулой (4.5.1) и (4.5.23).

при θ → −∞. Эти зависимости приводят к асимптотическому решению уравнения Кортевега—де Вриза в виде:

При t → −∞, получаем θ2 → ∞ и exp {θ2} → ∞, а из (4.5.23) находим асимптотику для F

F = exp {θ2} [1 + exp {θ1 + A12}] ,

которая приводит к решению уравнения Кортевега—де Вриза в виде

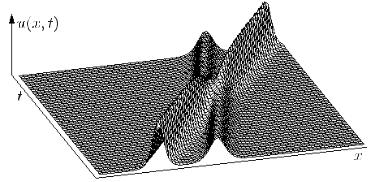
Из сравнения (4.5.24) и (4.5.25) следует, что каждый из солитонов после взаимодействия отличается на величину A12/2, характеризующую сдвиг фаз. На рис. 4.1. иллюстрируется процесс взаимодействия двух солитонов уравнения Кортевега—де Вриза.

Рис. 4.1. Взаимодействие двух солитонов Кортевега—де Вриза

По аналогии с приведенным выше двухсолитонным решением можно построить трехсолитонное решение уравнения Кортевега—де Вриза. С этой целью для f1 берется выражение (4.5.15) при N = 3:

(4.5.26)

тогда для f2 получается решение

f2 = exp {θ1 + θ2 + A12} + exp {θ1 + θ3 + A13} +

(4.5.27)

+ exp {θ2 + θ3 + A23},

224 Глава 4. Методы решения интегрируемых уравнений

причем в данном случае равным нулю оказывается fn при n 4. Подстановка (4.5.26), (4.5.27) и (4.5.29) в (4.5.7) приводит к

трехсолитонному решению уравнения Кортевега—де Вриза.

Эта процедура может быть продолжена для произвольного целого N .

4.6.Простейшие решения модифицированного уравнения Кортевега—де Вриза

Покажем, что решения модифицированного уравнения Кортевега—де Вриза

выражается через эллиптическую функцию Якоби. Уравнение (4.6.1) в переменных (4.6.2) становится обыкновенным дифференциальным уравнением, которое после интегрирования по z принимает вид:

4.6. Простейшие решения модифицированного уравнения 225

где C1 — постоянная интегрирования. Уравнение (4.6.3) относится к классу уравнений вида (4.2.1) и после умножения на yz может

Для того чтобы уравнение (4.7.2) стало обыкновенным дифференциальным уравнением относительно w(z), должны выполняться соотношения

Значения постоянных C1 и C2, вообще говоря, можно выбрать произвольными. Однако из соображений удобства возьмем следующие значения C1 = C2 = 3−1/3. При этом уравнение (4.7.5)

где w(z) — решения второго уравнения Пенлеве (4.7.7). Используя решение (4.7.8), нетрудно восстановить группу

преобразований растяжения, которая допускается модифицированным уравнением Кортевега—де Вриза. Соответствующий инфинитезимальный оператор имеет вид

228 Глава 4. Методы решения интегрируемых уравнений

4.8.Решения уравнения Кортевега—де Вриза пятого порядка в переменных бегущей волны

Используя переменные бегущей волны, найдем решения уравнения Кортевега—де Вриза пятого порядка, имеющего вид [128]

ut − 6β u ux + β uxxx − 20 ux uxx − 10 u uxxx+

(4.8.1)

+30 u2 ux + uxxxxx = 0.

Это уравнение относится к классу точно решаемых уравнений, для которого решение задачи Коши может быть получено с помощью метода обратной задачи рассеяния. Однако уравнение (4.8.1) допускает группы преобразований сдвига по x и t, поэтому решения этого уравнения можно искать в переменных бегущей волны.

Будем искать решения в виде

(где ϕ0 — произвольная постоянная), тогда после интегрирования по z из (4.8.1) приходим к обыкновенному дифференциальному уравнению [46, 121]

yzzzz − 10yyzz − 5yz2 + 10y3 + β(yzz − 3y3) + δy + μ = 0. (4.8.3)

В (4.8.3) δ = −C0 и μ обозначены как постоянные интегрирования.

Общее решение уравнения (4.8.3) имеет полюса второго порядка, и частные решения (4.8.3) можно искать в виде [39, 94]

y(z) = a0 th2(kz) + a1 th(kz) + a2, z = x − C0t + ϕ0. (4.8.4)

Уравнение (4.8.3) имеет два класса решений вида (4.8.4).

В первом случае коэффициенты a0, a1, a2, δ и μ определяются выражениями

a0 = 2k2, a1 = 0, a2 = const,

δ = 6βa2 − 80a2k2 − 30a22 + 104k4 ,

(4.8.5)

μ = 20a32 − 3βa22 + 80a22k2 − 64a2 k4− −4βk4 + 32k6 − 8βa2k2.

Второе семейство решений определяется следующими значениями постоянных

Из формул (4.8.5) и (4.8.6) следует, что уравнение (4.8.3) имеет частные решения в виде уединенных волн (4.8.4). Уравнение (4.8.3), как и (4.8.1), является точно решаемым уравнением, и поэтому найденные решения являются солитонными решениями. Однако в этой связи можно ожидать, что общее решение уравнения (4.8.3) существует.

Решение уравнения (4.8.3) при β = 0 впервые было найдено Драхом [98]. Затем оно было переоткрыто Дубровиным и Косгрове [22, 94].

230 Глава 4. Методы решения интегрируемых уравнений

Найдем решение уравнения (4.8.3) при β = 0. Заметим, что уравнение (4.8.3) не содержит третью производную, и в соответствии с теорией последнего множителя Якоби уравнение имеет последний множитель, равный единице [18, 94]. Поэтому для того, чтобы найти решение уравнения (4.8.3) в квадратурах, требуется найти два первых интеграла.

Один из первых интегралов уравнения находится после умножения (4.8.3) на yz :

yz yzzz − 12 yzz2 − 5 y yz2 + 52 y4 + β2 (yz2 − 2 y3)+

(4.8.7)

+ δ2 y2 + μ y = K1,

где K1 и далее K2, K3 и K4 — произвольные постоянные. Второй интеграл найти сложнее. Для этих целей можно ис-

пользовать полиномы с неопределенными коэффициентами [46]. Суть этого подхода заключается в следующем. На первом шаге предполагается, что в уравнении (4.8.3) β = δ = μ = 0. В этом

a0 = 2 и a0 = 6.

Еще один первый интеграл, соответствующий уравнению (4.8.3), ищем сначала для уравнения (4.8.8). Все слагаемые уравнения (4.8.8) имеют один и тот же порядок полюса в точке z = z0, равный 6. Естественно ожидать, что первый интеграл для уравнения (4.8.8) имеет слагаемые с одинаковым порядком полюса в