Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Кудряшов Методы нелинейной математич 2008

.pdf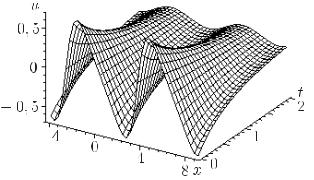

Скачиваний:

518

Добавлен:

16.08.2013

Размер:

1.5 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 2526 / 3626 27 28 29 30 31 32 33 34 35 36 > Следующая >>>

5.1. Метод укороченного разложения

251

из уравнений (5.1.22) и (5.1.23) имеем решение для F (x, t) в виде

g x

F5(x, t) = c1 + c2 exp

k t

−

c2 sin

'kx2

−

( + c3 cos

'kx2

−

( .

√

gtk√2

√2

gtk√2

(5.1.38)

Решение уравнения (5.1.12) в этом случае находится по формуле (5.1.18)

u = −	∂ lg F5(x, t)	.	(5.1.39)
	∂x

Из (5.1.38) следует, что решение u(x, t) является периодической функцией от x. Эволюция начального возмущения от времени показана на рис. 5.1.

Рис. 5.1. Зависимость от x и t периодического решения уравнения Бюргерса—Хаксли (5.1.12), полученного с учетом функции (5.1.38)

252 Глава 5. Методы построения точных решений

5.1.3.Точные решения уравнения Кортевега—де Вриза—Бюргерса

Применим метод укороченного разложения для построения точных решений уравнения Кортевега—де Вриза—Бюргерса:

ut + u ux + β uxxx = ν uxx.

(5.1.40)

С помощью переменной бегущей волны

u(x, t) = y(z), z = x − c0 t + ϕ0,

(5.1.41)

уравнение (5.1.40) после интегрирования по z принимает вид

C1 − C0 y + 12 y2 + β yzz − ν yz = 0.

Общее решение уравнения (5.1.42) существует при

	C1 =				1		C02 −	18 ν4
					2			625 β2
и имеет вид [39]:
			6ν2
	y = C0 +					+ a3 C32 exp (−2 a ξ)
			25β
	(C3 exp (−a ξ) + C2, 0 − 1),
где		13							31
a = −	(60 ν2 β2)			,			ξ =	(60 ν2 β2)		z,
	5 β							ν

(5.1.42)

(5.1.43)

(5.1.44)

(x) — эллиптическая функция Вейерштрасса.

Будем искать решение уравнения (5.1.40), используя разложение по новым функциям. Укороченное уравнение, состоящее из ведущих членов уравнения Кортевега—де Вриза—Бюргерса, имеет вид

u ux − β uxxx = 0.

(5.1.45)

5.1. Метод укороченного разложения

253

Подставляя u = u0 F p в (5.1.45), находим p = −2, и поэтому решение ищем в виде

u =	u0	+	u1	+ u2, F = F (x, t).	(5.1.46)
	F 2		F

Используя формулу (5.1.46), из (5.1.40) после приравнивая нулю выражений при одинаковых степенях F (x, t), получаем переопределенную систему уравнений

u0 = −12 β Fx

(5.1.47)

(5.1.48)

u1 = 12 β Fxx −

ν Fx,

Fxxx

6 ν Fxx

F 2

ν2

(5.1.49)

u2 +

+ 4 β

−

− 3 β

−

= 0,

F 2

25 β

ν Ft

Fxt

12νβ Fxxx

Fxx

FtFxx

− 2 β

− 3 β u2

−

Fx2

−

3 ν2 Fxx

6 ν β Fxx

− 5 β2

Fxxxx

+ 2

β2

Fxxx Fxx

−

(5.1.50)

−

β u2,x +

u2 = 0,

(u1)t + u1 (u2)x + u2 (u1)x + β (u1 )xxx − ν (u1 )xx = 0,

(5.1.51)

(u2)t + u2 (u2)x + β (u2)xxx − ν (u2)xx = 0.

(5.1.52)

Предопределенная система уравнений (5.1.49)—(5.1.52) является громоздкой и трудной для изучения. Однако можно заметить, что в эту систему уравнений входят только производные функции F (x, t), и поэтому, полагая [41]

254 Глава 5. Методы построения точных решений

F (x, t) = 1 + c1 exp{k x − ω t}, u2(x, t) = c2

(5.1.53)

(c1 и c2 — произвольные постоянные), от системы дифференциальных уравнений приходим к системе алгебраических уравнений


		β				3		6	2ν					ν2k				ω			(5.1.54)
		β		k			− 5 k		2ν		− 25 β + c2 k −							ω		= 0,	(5.1.54)
				k			− 5 k				− 25 β + c2 k −									= 0,
18	β ν k3 − 3				β c2 k2 +					1		ω ν − 3 β ω k +							1	c2 ν k−

5										5									5		(5.1.55)
							3	k2ν2 − 3 k4β2 = 0,													(5.1.55)
					−		3
					−		25
		6										1					1
	k4β2 −		k3ν β + k2c2									β +				k2ν2 −		kc2 ν−
	k4β2 −	5	k3ν β + k2c2									β +			5	k2ν2 −	5	kc2 ν−			(5.1.56)
						−kβ ω +						1	ν ω = 0.								(5.1.56)
												1
												5

Решив систему алгебраических уравнений (5.1.54)—(5.1.56) относительно k и ω, получаем зависимости k и ω от парамет-

ров ν и β:			ν
k1,2 =				,			(5.1.57)

			5 β
ω1,2 = −	6	ν3			ν c2		(5.1.58)
						.
	125	β2			5 β

С учетом выражений для коэффициентов u0 и u1 решение уравнения Кортевега—де Вриза—Бюргерса можно представить

формулой
u(x, t) = C		−		12 ν	∂ (1 + exp{k x − ω t + ϕ0})		+
u(x, t) = C	2			5			+
	2			5	∂ x		(5.1.59)
			∂2 (1 + exp{k x − ω t + ϕ0})				(5.1.59)
+ 12 β			∂2 (1 + exp{k x − ω t + ϕ0})			,
					∂ x2

5.1. Метод укороченного разложения

255

где значения k и ω определяются выражениями (5.1.57) и (5.1.58). Вычислив производные в (5.1.59), решение (5.1.59) можно представить в виде

u(x, t) = C2 +	12 β k2 ekx−ωt+ϕ0			12 ν kekx−ωt+ϕ0
			−				−
	1 + ekx−ωt+ϕ0			5	1 + ekx−ωt+ϕ0
			(5.1.60)
	−	12 β k2 e2 kx−2 ωt+2 ϕ0
						.
		(1 + ekx−ωt+ϕ0 )2

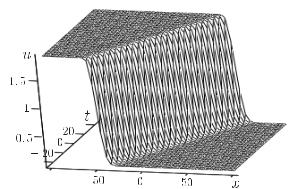
Рис. 5.2. Зависимость от x и t решения (5.1.60) уравнения Кортевега— де Вриза—Бюргерса (5.1.40)

Решение (5.1.60) уравнения (5.1.40) представляет собой кинк постоянной амплитуды, распространяющийся по среде с постоянной скоростью. График решения представлен на рис. 5.2.

256 Глава 5. Методы построения точных решений

5.2.Метод экспоненциальной функции для поиска точных решений нелинейных дифференциальных уравнений

Метод экспоненциальной функции (Exp — funtion method) является следствием метода Вайса—Табора—Карневейля, хотя реально был открыт как самостоятельный метод поиска точных решений нелинейных дифференциальных уравнений.

Заметим, что подстановка (5.1.53) в укороченное разложе-

ние приводит	к		логарифмическим производным от функции
F = 1 + exp k z		}	, где z = x	−	ω k−1 t + ϕ0 k−1	. Как следствие
{

этого обстоятельства в решении (5.1.60) появляется функция вида


G(x, t) =	ekx−ωt+ϕ0			(5.2.1)
			.
	1 + ekx−ωt+ϕ0
При этом степень функции G(x, t)		в решении (5.1.60) рав-
на порядку полюса общего	решения	уравнения		Кортевега—

де Вриза—Бюргерса. Дифференциирование фунцкии G(x, t) по t и по x повышает ее степень на единицу и приводит к соотношениям

Gt = −ω G + ω G2 ,	(5.2.2)
Gx = k G − k G2.	(5.2.3)

Дифференцируя по x выражение (5.2.3), получаем соотношения для старших производных функции G(x, t):

Gxx = k2G − 3 k2G2 + 2 k2G3,	(5.2.4)
Gxxx = k3G − 7 k3 G2 + 12 k3G3 − 6 k3 G4,	(5.2.5)
Gxxxx = k4G − 15 k4 G2 + 50 k4G3 − 60 k4 G4 + 24 k4 G5.	(5.2.6)

В связи с этими замечаниями метод укороченного разложения можно корректировать, что и приводит к методу экспоненциальной функции.

5.2. Метод экспоненциальной функции

257

Пусть задано нелинейное дифференциальное уравнение, решение которого имеет полюс p-го порядка

E (u, ut, ux, . . . , x, t) = 0.

(5.2.7)

Тогда точные решения этого уравнения можно искать в виде разложения по степеням логарифмической производной от функции F = 1 + exp {k x − ω t + ϕ0}:

p
u(x, t) = Aj G(x, t)j .	(5.2.8)

j=0

При проведении вычислений следует учесть соотношения (5.2.3), (5.2.4), (5.2.5) и (5.2.6).

5.2.1.Точные решения уравнения Колмогорова—Петровского—Пискунова

Используя метод экспоненциальной функции, найдем точные решения уравнения Колмогорова—Петровского—Пискунова [80]:

ut = δ uxx + α u − u2.

(5.2.9)

Из сравнения ведущих членов уравнения находим, что его решение имеет полюс второго порядка, и поэтому решение можно искать в виде

u(x, t) = A0 + A1 G(x, t) + A2 G(x, t)2 .

(5.2.10)

Подставляя выражение (5.2.10) в уравнение (5.2.9) и приравнивая к нулю выражения при одинаковых степенях G(x, t), получаем систему алгебраические уравнений

A2 − 6 δ k2 = 0,	(5.2.11)
10 δ A2k2 + 2 A1A2 − 2 δA1k2 + 2 A2ω = 0,	(5.2.12)

258 Глава 5. Методы построения точных решений


2 A0 A2 − 2 A2	ω + A1	2 − α A2 + 3 δ A1k2+			(5.2.13)
+A1ω − 4 δ A2k2 = 0,
2 A0A1	− α A1	− δ A1k2 − A1ω = 0,			(5.2.14)
		1			(5.2.15)
	9 δ2 k4 −			α2 = 0.
	9 δ2 k4 −		4	α2 = 0.

Решив эту систему алгебраических уравнений, получаем значения коэффициентов и параметров разложения решения

A2 = 6δ k2	, A1 = −6 δ k2 −	6	ω, A0	= α,	(5.2.16)
		5
	ω1,2 = 5 δ k2,				(5.2.17)

√√

			6 α δ					i 6 α δ	(5.2.18)
k1,2 = δ							k3,4 =	δ .

Подставляя (5.2.16) и ω = ω1 в (5.2.10), получим решение
u (x, t) = −3 δ k2 +				1		α + 6 δ k2G (x, t)2 .			(5.2.19)

					2
В случае (5.2.16) и ω = ω2 решение принимает вид
1				δ k2 G (x, t) + 6 δ k2G (x, t)2 ,
u (x, t) = 3 δ k2 +		α − 12							(5.2.20)
	2

где функция G(x, t) определяется выражением (5.2.1), а параметр k принимает одно из значений (5.2.18).

Можно заметить, что полученные решения уравнения Колмогорова—Петровского—Пискунова зависят от переменной бегущей волны, поэтому решение этого уравнения можно искать, используя переменную бегущей волны с самого начала.

5.2. Метод экспоненциальной функции

259

5.2.2.Точные решения уравнения Гарднера с учетом диссипации

Используя метод экспоненциальной функции, найдем точные решения нелинейного уравнения Гарднера

ut + u ux + u2 ux + β uxxx − ν uxx = 0.

(5.2.21)

Уравнение (5.2.21) не относится к классу точно решаемых. Однако имеет некоторые специальные решения. Решение уравнения будем искать, используя переменную бегущей волны

u(x, t) = y(z), z = x − c0t,

(5.2.22)

где y(z) удовлетворяет уравнению

c1 − c0y +	1	y2 +	1	y3 + β yzz − ν yz = 0	(5.2.23)
	2		3

(c1 — постоянная интегрирования).

Укороченное уравнение, сооветствующее уравнению (5.2.23), имеет вид

	1	y3	+ β yzz = 0.			(5.2.24)
3

Из уравнения (5.2.24) видно, что решение имеет полюс перво-
го порядка, поэтому y(z) ищем в виде
y(z) = A0 + A1 G(z),						(5.2.25)
где G(z) имеет вид
G(z) =				exp {k z}	,	(5.2.26)
				1 + exp {k z}

причем G(z) удовлетворяет уравнениям (5.2.3), (5.2.4)
Gz = k G − k G2,						(5.2.27)
Gzz = k2G − 3 k2G2 + 2 k2G3.

260 Глава 5. Методы построения точных решений

Подставляя (5.2.25) в (5.2.23), получаем уравнение


			1		A13 − 12 β2 A1k2				G4+
				3	A13 − 12 β2 A1k2				G4+
			1					1
	+ c1 − C0 A0 +						A03 +		A02 G+
	+ c1 − C0 A0 +					3	A03 +	2	A02 G+	(5.2.28)
+	1	A1	2 + 18 β2 A1k2 + ν A1k + A0A12 G3+

	2
+ A0A1 − C0 A1 + A02A1 − 6 β2A1k2 − ν A1 k G2 = 0.

Приравнивая нулю выражения при одинаковых степенях функции G(z), находим выражения для коэффициентов разложения (5.2.25) и параметров уравнения (5.2.23)

A(1,2) =

β k,

A(1,2)

ν + 18 β2 k 3 β

(5.2.29)

6 β

C0 =

ν2 − 9 β2 + 108 β4 k2

36 β2

(5.2.30)

9 ν2

β ± 648 β4 k2ν − 27 β3 2 ν3 + 972 β5 k2

−

648 β3

Точные решения уравнения (5.2.23) с учетом (5.2.30) выражаются формулой

y(z) =	±	ν 3 β + 18 β2 k	6 β kekz	.	(5.2.31)
		6 β
			1 + ekz

Решения (5.2.31) представляют собой уединенные волны в форме кинков.

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 23 24 2526 / 3626 27 28 29 30 31 32 33 34 35 36 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.08.20139.31 Mб450Крючков Основы учёта,контроля 2007.pdf
#
16.08.20132.37 Mб196Крючков Технические аспекты ядерного нераспространения 2010.pdf
#
16.08.2013864.18 Кб34Ктитров Администрирование ОЦ УНИХ 2007.pdf
#
16.08.20131.06 Mб53Ктитров Командный язык ОЦ Уних 2007.pdf
#
16.08.20131.93 Mб138Ктитров Расчет установившихся режимов и переходных процессов в нелинейных 2008.pdf
#
16.08.20131.5 Mб518Кудряшов Методы нелинейной математич 2008.pdf
#
16.08.20131.51 Mб193КузминАМ Основы теории критичности 2008.pdf
#
16.08.20131.79 Mб77Кулик Елементы теории принятия решений 2010.pdf
#
16.08.20131.87 Mб99Кулик Теория принятия решений 2007.pdf
#
16.08.201310.8 Mб226Курнаев Введение в пучковую електронику 2008.pdf
#
16.08.201310.79 Mб69Лабораторный практикум Компютерное модел 2007.pdf