Кудряшов Методы нелинейной математич 2008

282 Глава 5. Методы построения точных решений

Уравнение (5.4.59) при этом запишется в виде

Решения (5.4.66) и (5.4.71) уравнения (5.4.53) являются периодическими волнами. Более детальное обсуждение применения метода простейших уравнений можно найти в работе [124].

5.5.Применение многоугольников при построении точных решений

Одной из трудностей применения метода простейших уравнений для построения точных решений нелинейных дифференциальных уравнений является выбор простейшего уравнения. В ряде случаев в качестве простейших уравнений можно взять хорошо известные точно решаемые нелинейные обыкновенные дифференциальные уравнения: уравнение Риккати (5.4.5), уравнение для эллиптической функции Якоби (5.4.11) или уравнение для эллиптической функции Вейерштрасса (5.4.12). Однако во многих случаях эта трудность становится препятствием применения метода простейших уравнений, в преодолении которой может существенно помочь применение многоугольников, которые часто называют многоугольниками Ньютона [11, 12, 130].

Работа Ньютона по анализу алгебраического уравнения с использованием графической иллюстрации выполнена в 1711 году. Сам Ньютон считал эту работу одной из самых важных. Однако споры о роли самого Ньютона в открытии многоугольника, называемого его именем, не утихают до настоящего времени. Повидимому, это связано с тем, что сам Ньютон при анализе алгебраического уравнения рассмотрел лишь одно ребро ломаной.

Целиком выпуклая ломаная была рассмотрена Пюизе. Работа самого Пюизе не содержала ссылки на Ньютона, и остается неясным ответ на вопрос, был ли знаком Пюизе с работой Ньютона. Возможно, поэтому многие исследователи многоугольник Ньютона часто называют многоугольником Ньютона—Пюизе [3].

Применение многоугольников для решения различных задач исследования нелинейных обыкновенных дифференциальных уравнений основано на установлении соответствия между обыкновенным дифференциальным уравнением и многоугольником на плоскости, который как раз и называется многоугольником Ньютона.

Пусть задано нелинейное обыкновенное дифференциальное уравнение полиномиального вида

Каждому члену (моному) дифференциального уравнения (5.5.1) ставится в соответствие точка на плоскости по следующему правилу [11, 12, 130]

где C1, C2 — произвольные постоянные. При умножении мономов их координаты складываются. Множество точек на плоскости, сооветствующее дифференциальному уравнению, образует так называемый носитель. Соединяя все внешние точки носителя, получаем многоугольник Ньютона на плоскости. Таким образом, каждому обыкновенному дифференциальному уравнению (5.5.1) ставится в соответствие многоугольник L1 на плоскости [11, 12, 127, 128, 129].

Пусть решение y(z) исходного уравнения выражается через решения Y (z) простейшего уравнения

284 Глава 5. Методы построения точных решений

Подстановка (5.5.3) в уравнение (5.5.1) ведет к новому дифференциальному уравнению, которому также можно поставить в соответствие многоугольник Ньютона на плоскости. Обозначим этот многоугольник L2. Анализируя многоугольник L2, можно построить многоугольник Ньютона L3, соответствующий про-

нормальные векторы, то соответствующие асимптотики совпадают вплоть до значения коэффициентов [11, 12]. Под внешним нормальным вектором мы имеем в виду вектор, который направлен вне многоугольника. Следовательно, пригодный многоугольник L3 имеет все или несколько ребер, параллельных многоугольнику L2. Кроме того, в случае, когда многоугольник L3 передвигается по плоскости, его ребра должны перекрывать носитель преобразованного уравнения.

Предположим, что многоугольник L3 построен. Тогда анали-

ˆ

где R — дифференциальный оператор, то это означает, что для любого решения Y (z) простейшего уравнения (5.5.4) существует решение (5.5.3) исходного нелинейного дифференциального уравнения (5.5.1).

При выборе простейшего уравнения естественным является требование о том, что порядок простейшего уравнения выбирается меньшим, чем порядок исходного уравнения, соответствующего многоугольнику L2. Самыми важными простейшими уравнениями являются такие уравнения, общие решения которых не имеют подвижных критических особых точек. Если общее (или

частное) решение простейшего решения находится, то для изучаемого уравнения по формуле (5.5.3) находятся точные решения.

Применение многоугольников Ньютона для построения точных решений нелинейных дифференциальных уравнений можно сформулировать в виде следующих шести шагов.

Первый шаг. Построение многоугольника L1, соответствующего исходному уравнению.

Второй шаг. Определение порядка подвижного полюса общего решения изучаемого уравнения и написание преобразования (5.5.3), связывающего решения уравнений.

Третий шаг. Построение многоугольника L2 соответствующего преобразованному уравнению.

Четветый шаг. Построение многоугольника L3, характеризующего простейшее уравнение.

Пятый шаг. Выбор простейшего уравнения с неизвестными параметрами, соответствующего многоугольнику L3.

Шестой шаг. Определение коэффициентов преобразования (5.5.3) и параметров простейшего уравнения.

В случае, когда полюс общего решения простейшего уравнения совпадает с полюсом исходного уравнения, простейшее уравнение часто выбирается без преобразования исходного уравнения (5.5.3). В этом случае формула (5.5.3) становится тождественной подстановкой: y(z) ≡ Y (z).

5.5.1.Точные решения обобщенного уравнения Курамото—Сивашинского

Продемонстрируем применение метода многоугольников для построения точных решений обобщенного уравнения Курамото— Сивашинского [130]

286 Глава 5. Методы построения точных решений

и интегрируя полученное уравнение по переменной z, приходим к уравнению

где постоянная интегрирования полагается равной нулю. Точные решения уравнения (5.5.10) находятся в соответствии со следую-

щей теоремой.

Теорема 5.1. Пусть y(z) — решение уравнения

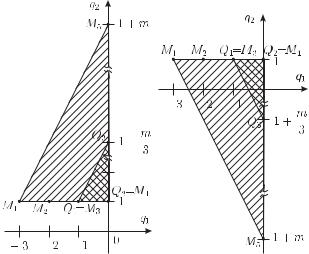
Доказательство. Мономам уравнения (5.5.10) соответствуют следующие точки на плоскости: M1 = (−3, 1),

M2 = (−2, 1), M3 = (−1, 1), M4 = (0, 1) и M5 = (0, m + 1). Многоугольник L1, соответствующий уравнению (5.5.10), является большим треугольником на рис. 5.7 (здесь левый треугольник соответствует m > 0 и, правый треугольник соответствует m < 0). Подходящий многоугольник L3 может быть найден без преобразования исходного уравнения это малый треугольник на рис.

4.10, который содержит точки: Q1 = (−1, 1), Q2 = M4 = (0, 1), и

Q3 = (0, 1 + m3 ).

Рис. 5.7. Многоугольники Ньютона, соответствующие дифференциальным уравнениям (5.5.10) и (5.5.13) при m > 0 (слева) и при m < 0 (справа)

Простейшее уравнение, соответствующее многоугольнику L3, можно представить в виде

C0 = 1/ 27. Однако при m → ∞ скорость C0 → 0.

Полагая m = 1 в (5.5.24), получим решение в виде уединенной

уравнения Курамото—Сивашинского представляет собой кинк [41, 45, 113, 120, 124]. Некоторые другие решения обобщенного уравнения Курамото—Сивашинского (5.5.6) получены в работе [131].

5.5.2.Автомодельные решения уравнения Кортевега— де Вриза пятого порядка

Используя многоугольники Ньютона, найдем решения уравнения Кортевега—де Вриза пятого порядка [130]

290 Глава 5. Методы построения точных решений

ut + uxxxxx − 10 u uxxx − 20 uxuxx + 30 u2 ux = 0. (5.5.27)

Решения уравнения (5.5.27) будем искать, используя автомодельные переменные

где y(z) удовлетворяет нелинейному обыкновенному дифференциальному уравнению

yzzzzz − 10 y yzzz − 20 yz yzz + 30 y2 yz − z yz − 2 y = 0. (5.5.29)

Результаты можно сформулировать в виде следующей теоре-

мы.

Теорема 5.2. Пусть Y (z) — решение уравнения

является решением уравнения (5.5.29).

Доказательство. Мономам уравнения (5.5.29) соответствуют точки на плоскости: M1 = (−5, 1), M2 = (−3, 2), M3 = (−3, 2), M4 = (−1, 3), M5 = (0, 1) и M6 = (0, 1). Носитель уравнения (5.5.29) определяется точками: Q1 = M1 = (−5, 1), Q2 = M4 = = (−1, 3), Q3 = M5 = M6 = (0, 1) и Q4 = M2 = M3 = (−3, 2). Соответствующий многоугольник L1 представлен на рис. 5.8.

Общее решение уравнения (5.5.29) имеет полюс второго по-