
- •Фгоу впо «Волгоградская академия государственной службы»
- •1.2. Цели и задачи учебной дисциплины.
- •1.3. Требования к уровню освоения дисциплины (знания, умения, навыки).
- •1.4. Тематический план курса «математика» (174 ч.)
- •1.5. Учебно-методическое обеспечение учебной дисциплины
- •Тема 6. Понятие функции. Способы задания и основные свойства функций.
- •Тема 7. Предел последовательности и функции. Правила вычисления пределов.
- •Тема 8. Замечательные пределы. Непрерывность функции. Основные теоремы о непрерывных функциях. Точки разрыва и их классификация.
- •Тема 9. Задачи, приводящие к производной. Понятие производной функции.
- •Тема 10. Производная неявных и параметрических функций. Производные высших порядков.
- •Тема 11. Понятие дифференциала функции.
- •Тема 12. Основные теоремы о дифференцируемых функциях. Теоремы Ферма, Ролля, Лагранжа и Коши. Правило Лопиталя-Бернулли раскрытия неопределенностей вида и.
- •Тема 13. Полное исследование функций и построение графиков.
- •Тема 14. Первообразная и неопределенный интеграл. Свойства интеграла. Таблица неопределенных интегралов.
- •Тема 15. Основные методы интегрирования.
- •Тема 16. Понятие определенного интеграла. Свойства и правила вычисления определенного интеграла.
- •Тема 17. Приложения определенного интеграла. Несобственные интегралы.
- •Планы семинарских и практических занятий
- •Тема 1. Операции над матрицами. Определители третьего порядка. (2 часа)
- •Тема 2. Определители четвертого и выше порядков. Элементарные преобразования определителей. Обратная матрица. (4 часа)
- •Тема 3. Ранг матрицы.(4 часа)
- •Тема 8. Замечательные пределы. Основные эквивалентные функции (4 часа).
- •Тема 9. Определение производной. Геометрический смысл. Основные правила дифференцирования. Таблица производных элементарных функций.(2 часа)
- •Тема 10. Производные неявных и параметрических функций. Логарифмическое дифференцирование. Производные высших порядков.(2 часа)
- •Тема 11. Дифференциал функции. Приложение производной в теории пределов. (2 часа)
- •Тема 12. Общая схема исследования функций и построения их графиков.(2 часа)
- •Тема 13. Контрольная работа.(2 часа)
- •Тема 14. Неопределенный интеграл. Свойства неопределенного интеграла. Интегралы от основных элементарных функций. Основные методы интегрирования.(2 часа)
- •Тема 15. Основные методы интегрирования: интегрирование по частям.(2 часа)
- •Тема 16. Определенный интеграл. Формула Ньютона-Лейбница. Методы интегрирования. Геометрические приложения определенного интеграла. (4 часа)
- •Темы, выносимые на самостоятельное изучение:
- •Тема 1. Основы теории множеств.
- •Тема 2. Элементы аналитической геометрии.
- •Вопросы к зачету:
- •Материалы текущего, промежуточного и итогового контроля Вопросы к аттестации
- •Контрольная работа № 1
- •Тема 19. Экстремум функций нескольких переменных. Наибольшее и наименьшее значения функции. Условный экстремум.
- •Тема 20. Условный экстремум функций нескольких переменных.
- •Тема 21. Основные понятия теории дифференциальных уравнений. Дифференциальные уравнения первого порядка.
- •Тема 22. Линейные неоднородные дифференциальные уравнения первого порядка.
- •Тема 23. Линейные однородные дифференциальные уравнения второго порядка. Линейные неоднородные дифференциальные уравнения второго порядка с правой частью специального вида.
- •Тема 24. Линейные неоднородные дифференциальные уравнения второго порядка. Метод Лагранжа.
- •Тема 30. Алгебра событий. Теоремы сложения и умножения вероятностей событий.
- •Тема 31. Формула полной вероятности. Формула Байеса.
- •Планы семинарских и практических занятий
- •Тема 1. Функции нескольких переменных. Частные производные. Дифференциал. (4 часа)
- •Тема 2. Экстремум функций двух переменных. Наибольшее и наименьшее значения функции. (2 часа)
- •Тема 3. Дифференциальные уравнения. Общее решение дифференциального уравнения. Задача Коши. (2 часа)
- •Тема 4. Линейные неоднородные дифференциальные уравнения первого порядка. (2 часа)
- •Тема 5. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Уравнения однородные. Неоднородные уравнения с правой частью специального вида. (4 часа)
- •Тема 6. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод Лагранжа. (4 часа)
- •Тема 7. Числовые ряды. Определение сходимости ряда. Основные свойства рядов. Необходимый признак сходимости числового ряда.Достаточные признаки сходимости знакоположительных рядов. (4 часа)
- •Тема 8. Знакочередующиеся ряды. Теорема Лейбница.(2 часа)
- •Тема 9. Понятие функционального ряда. Область сходимости. Степенной ряд. Интервал и радиус сходимости степенного ряда.(2 часа)
- •Тема 10. Разложение функций в степенные ряды. Формула и ряд Тейлора. Формула и ряд Маклорена. Применение рядов в приближенных вычислениях. (2 часа)
- •Тема 11. Контрольная работа. (2 часа)
- •Тема 12. Классическое определение вероятности. Элементы комбинаторики. Алгебра событий. Теоремы сложения и умножения вероятностей. (2 часа)
- •Тема 13. Формула полной вероятности. Формула Байеса. (2 часа)
- •Тема 14. Последовательность независимых испытаний. Наивероятнейшее число появлений события в серии из n независимых испытаний. Асимптотические формулы.(2 часа)
- •Тема 15. Контрольная работа.(2 часа)
- •Тема 16. Дискретная и непрерывная случайная величина. Закон распределения. Числовые характеристики.(2 часа)
- •Тема 17. Классические законы распределения случайных величин. Биномиальный закон. Равномерное и показательное распределение. Нормальная случайная величина.(2 часа)
- •Темы, выносимые на самостоятельное изучение:
- •Тема 1. Самостоятельное решение задач по теории дифференциальных уравнений и теории рядов.
- •Тема 2. Самостоятельное решение задач по теории вероятностей.
- •Вопросы к экзамену:
- •Материалы текущего, промежуточного и итогового контроля Вопросы к аттестации
- •Контрольная работа № 1 Примерный вариант заданий
- •Контрольная работа № 2 Примерный вариант заданий
- •Примерный вариант экзаменационного билета
- •Список рекомендуемой литературы
- •Раздел 2. Методические рекомендации по изучению учебной дисциплины для студентов
- •2.1. Рекомендации по использованию материалов учебно-методического комплекса:
- •2.2. Пожелания к изучению отдельных тем курса
- •2. 3. Рекомендации по работе с литературой
- •2.4. Советы по подготовке к экзамену (зачету)
- •Раздел 3. Материалы тестовой системы или практикум по решению задач по темам лекций
- •Iсеместр
- •Примеры решения задач по темам 1 – 5
- •Примерный вариант практического задания по Темам 1 – 5.
- •Примеры решения задач по темам 6 – 13
- •Примерный вариант практического задания по Темам 6 – 13.
- •Примеры решения задач по темам 14 – 17
- •Примерный вариант практического задания по Темам 14 – 17.
- •IIсеместр
- •Примеры решения задач по темам 18 – 24
- •Примерный вариант практического задания по Темам 18 – 24.
- •Примеры решения задач по темам 25 – 28
- •Примерный вариант практического задания по Темам 25 – 28.
- •Примеры решения задач по темам 29 – 35
- •Примерный вариант практического задания по Темам 29 – 35.
- •Раздел 4. Словарь основных терминов (глоссарий)
Примеры решения задач по темам 29 – 35
Пример 1. Студент знает 15 вопросов из 30 в первом разделе курса и 25 из 40 вопросов второго раздела этого курса.
Найти вероятность того, что студент:
1) знает ответы на оба вопроса;
2) не знает ответов на оба вопроса;
3) знает ответ только на один вопрос в билете.
Решение. Обозначим общее число вопросов первого раздела курсаn1= 30, а количество выученных вопросов этого разделаm1= 15.
Общее число вопросов второго раздела курса — n2= 40, а количество выученных вопросов этого раздела (т.е. благоприятствующих хорошему ответу)m2= 25.
Далее введём обозначение событий. Пусть:
событие Aсостоит в том, что студент знает ответ на вопрос, случайным образом предложенный ему из первого раздела курса;
 — противоположное событие, состоит в
том, что студент не знает ответ на
вопрос, случайным образом предложенный
ему из первого раздела курса; событиеBсостоит в том, что студент знает
ответ на вопрос, случайным образом
предложенный ему из второго раздела
курса;
— противоположное событие, состоит в
том, что студент не знает ответ на
вопрос, случайным образом предложенный
ему из первого раздела курса; событиеBсостоит в том, что студент знает
ответ на вопрос, случайным образом
предложенный ему из второго раздела
курса;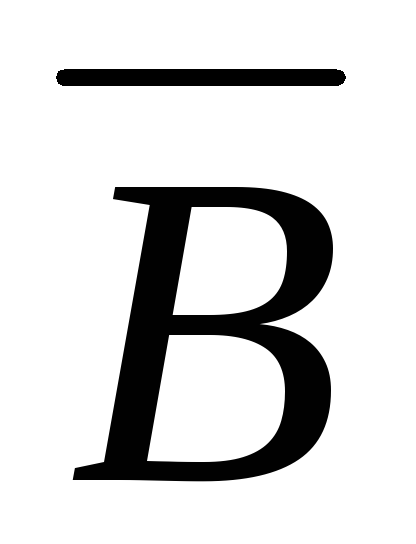 — противоположное событие, состоит в
том, что студент не знает ответ на
вопрос, случайным образом предложенный
ему из второго раздела курса.
— противоположное событие, состоит в
том, что студент не знает ответ на
вопрос, случайным образом предложенный
ему из второго раздела курса.
Вероятности событий AиBнайдём, пользуясь классическим определением вероятности:
![]() .
.
Вероятности противоположных событий
![]() и
и![]() определим, исходя из соотношения между
вероятностями противоположных событий
:
определим, исходя из соотношения между
вероятностями противоположных событий
:
![]() .
.
1. Для нахождения ответа на первый пункт введём обозначение ещё одного события:
пусть событие Cсостоит в том, что студент знает ответы на оба случайным образом предложенных ему вопроса из первого и второго разделов курса.
Опираясь на понятие произведения двух событий, видим, что C=AB.
Для нахождения вероятности события Cприменим теорему умножения вероятностей
независимых событий. Тогда![]() .
.
2. Для решения второго пункта задачи
введём ещё одно обозначение события:
событие Dсостоит в том, что студент
не знает ответы на оба случайным образом
предложенных ему вопроса из первого и
второго разделов. Используя понятие
произведения двух событий,![]() .
.
Для нахождения вероятности события Dприменим снова теорему умножения
вероятностей независимых событий. Тогда
![]() .
.
3. Для решения третьего пункта введём
ещё одно обозначение события: событие
Eсостоит в том, что студент знает
ответ только на один из двух случайным
образом предложенных ему вопросов из
первого или второго раздела курса. Это
сложное событие состоит из двух событий:
или студент знает ответ на случайный
вопрос из первого раздела и не знает
ответ на вопрос из второго раздела, т.е.![]() ,
или студент не знает ответ на вопрос из
первого раздела и знает ответ на вопрос
из второго раздела, т.е.
,
или студент не знает ответ на вопрос из
первого раздела и знает ответ на вопрос
из второго раздела, т.е.![]() .
.
Окончательно, событие
![]() .
.
Для нахождения вероятности этого события сначала применим теорему сложения вероятностей несовместных событий.
В нашем случае будет
![]() .
.
Теперь дважды применим теорему умножения вероятностей независимых событий:
![]() .
.
Подставляем числовые значения этих вероятностей, получим:
![]() .
.
Ответ. 1. Студент знает ответы на оба
предложенных вопроса с вероятностьюP(C) = ![]() .
2. Студент не знает ответов на оба
предложенных вопроса с вероятностью
.
2. Студент не знает ответов на оба
предложенных вопроса с вероятностью![]() .
3. Студент знает ответ на один из двух
предложенных ему вопросов с вероятностью
.
3. Студент знает ответ на один из двух
предложенных ему вопросов с вероятностью![]() .
.
Пример 2. Вероятность безотказной работы в течение гарантийного срока составляет для пылесоса 0,8 и для холодильника 0,95.
Какова вероятность того, что в течение гарантийного срока окажутся работоспособными:
1) оба прибора;
2) хотя бы один прибор?
Решение. Введём обозначение событий.
Пусть событиеAсостоит в том, что
пылесос не сломается в течение гарантийного
срока;![]() —
противоположное событие, состоит в том,
что пылесос сломается в течение
гарантийного срока; событиеBсостоит
в том, что холодильник не сломается в
течение гарантийного срока;
—
противоположное событие, состоит в том,
что пылесос сломается в течение
гарантийного срока; событиеBсостоит
в том, что холодильник не сломается в
течение гарантийного срока;![]() — противоположное событие, состоит в
том, что холодильник сломается в течение
гарантийного срока. Вероятности событийAиB нам даны в условии задачи:P(A)
= 0,80;P(B)
= 0,95. Вероятности противоположных событий
— противоположное событие, состоит в
том, что холодильник сломается в течение
гарантийного срока. Вероятности событийAиB нам даны в условии задачи:P(A)
= 0,80;P(B)
= 0,95. Вероятности противоположных событий![]() и
и![]() определим, исходя из соотношения между
вероятностями противоположных событий:
определим, исходя из соотношения между
вероятностями противоположных событий:
P(![]() )
= 1 –P(A)
= 1
– 0,80
= 0,20,
)
= 1 –P(A)
= 1
– 0,80
= 0,20,
P(![]() )
= 1 –P(B)
= 1
– 0,95
= 0,05.
)
= 1 –P(B)
= 1
– 0,95
= 0,05.
1. Для нахождения ответа на первый пункт введём обозначение ещё одного события: событие Cсостоит в том, что оба прибора не сломаются в течение гарантийного срока. Опираясь на понятие произведения двух событий, видим, чтоC=AB. Для нахождения вероятности событияCприменим теорему умножения вероятностей независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
P(AB) = P(A)P(B). Тогда P(C) = P(A B) = P(A)P(B) = 0,800,95 = 0,760.
2. Для решения второго пункта задачи введём ещё одно обозначение события:
событие Dсостоит в том, что в течение гарантийного срока хотя бы один прибор будет работать.
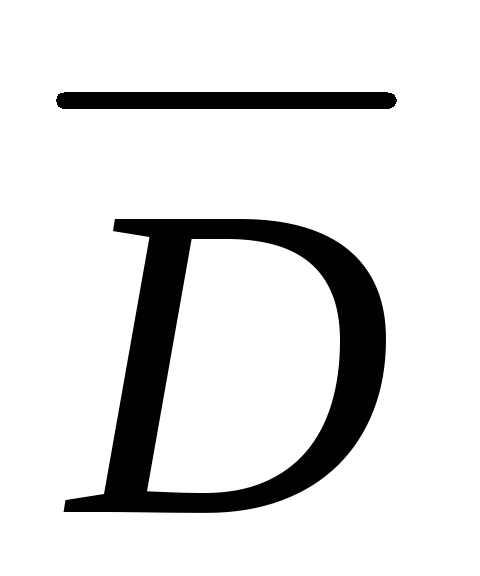 —противоположное
событие, состоит в том, что оба прибора
сломаются в течение гарантийного срока.
Используем понятие произведения двух
событий:
—противоположное
событие, состоит в том, что оба прибора
сломаются в течение гарантийного срока.
Используем понятие произведения двух
событий:
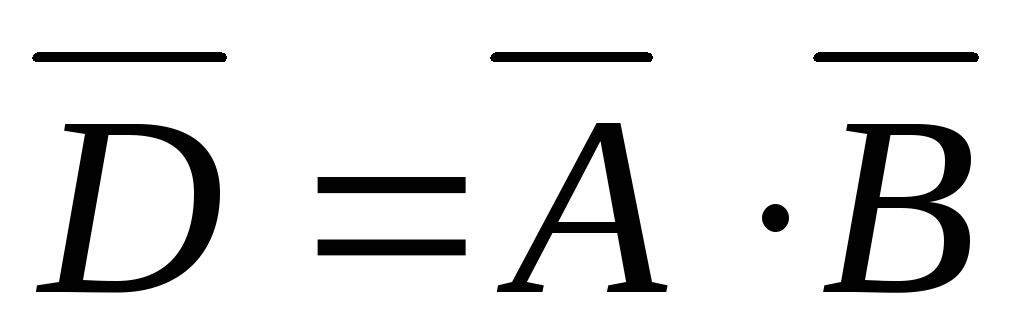 .
Для нахождения вероятности события
.
Для нахождения вероятности события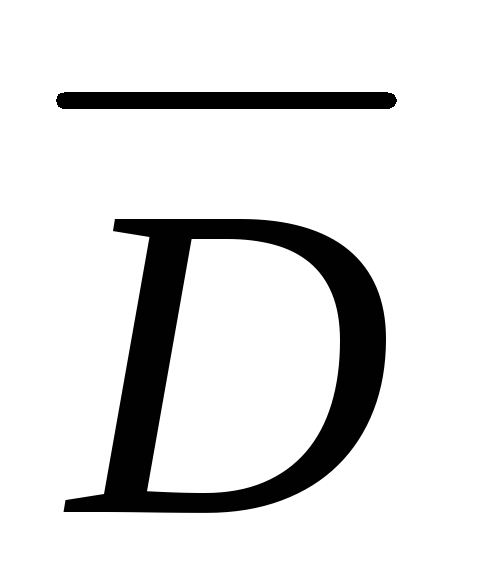 применим ту же теорему умножения
вероятностей независимых событий.
Тогда
применим ту же теорему умножения
вероятностей независимых событий.
Тогда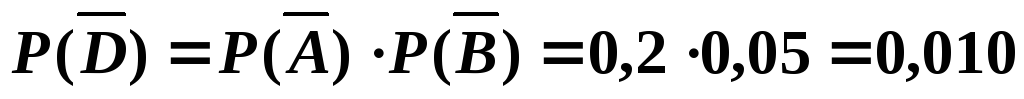 .
.
Но это вероятность противоположного
события
![]() ,
а нам надо узнать вероятность прямого
событияD, которую определим, пользуясь
соотношением между вероятностями
противоположных событий. Тогда вероятность
того, что будет работать хотя бы один
прибор:
,
а нам надо узнать вероятность прямого
событияD, которую определим, пользуясь
соотношением между вероятностями
противоположных событий. Тогда вероятность
того, что будет работать хотя бы один
прибор:
P(D)
= 1 – P(![]() )
= 1
– 0,010 = 0,990.
)
= 1
– 0,010 = 0,990.
Ответ. 1. Вероятность того, что пылесос и холодильник будут работать в течение гарантийного срока,P(C) = 0,76.
2. Вероятность того, что хотя бы один из приборов будет работать в течение гарантийного срока, P(D) = 0,99.
Пример 3. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит60% деталей отличного качества, а второй –84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что деталь произведена первым автоматом.
Решение. СобытиеA= {деталь оказалась отличного качества}. Гипотезы:
B1 — деталь изготовлена первым автоматом,B2 — деталь изготовлена вторым автоматом.
Найдем вероятности гипотез, исходя из
того, что производительность первого
автомата вдвое больше второго:
![]() .
.
![]() — вероятность того, что наудачу взятая
деталь будет отличного качества, при
условии, если она произведена первым
автоматом.
— вероятность того, что наудачу взятая
деталь будет отличного качества, при
условии, если она произведена первым
автоматом.![]() — вероятность того, что наудачу взятая
деталь будет отличного качества, при
условии, если она произведена вторым
автоматом.
— вероятность того, что наудачу взятая
деталь будет отличного качества, при
условии, если она произведена вторым
автоматом.
По условию задачи эти вероятности
соответственно равны
![]() .
.
Найдем вероятность P(A) по формуле полной вероятности:
![]()
Первое слагаемое соответствует доле вероятности изготовления деталей отличного качества первым автоматом. Тогда по формуле Бейеса имеем:
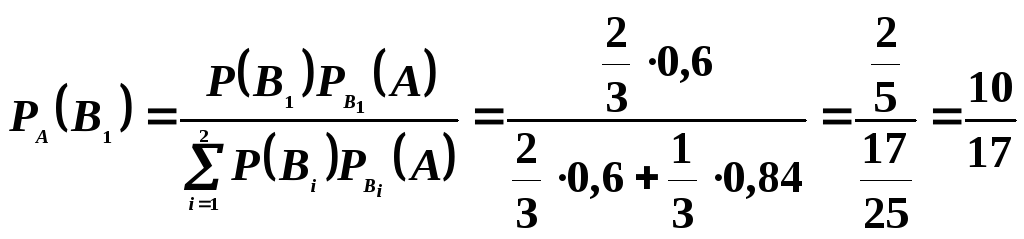 .
.
Ответ. Вероятность того, что взятая с конвейера деталь, которая оказалась отличного качества, произведена первым автоматом, равна10/17.
Пример 4. Вероятность того, что расход электроэнергии в течение одних суток не превысит установленной нормы, равна0,75. Найти вероятность того, что в ближайшие7суток расход электроэнергии не превысит нормы в течение4суток.
Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из7суток постоянна и равнаp =0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равнаq=1–p=1–0,75=0,25. По условию задачи количество повторных независимых испытаний, т.е. количество наблюдаемых суток,n =7,k =4. Используя формулу Бернулли, получаем:
![]() .
.
Ответ.Из100недель, взятых для наблюдения, в17случаях расход электроэнергии не превысит нормы в течение4суток.
Пример 5. Установлено, что в данном технологическом процессе в среднем90% выпускаемых изделий являются стандартными. При выборочном контроле качества продукции было случайным образом отобрано400изделий. Каково наивероятнейшее число стандартных изделий среди400отобранных и чему равна соответствующая этому событию вероятность? Какова вероятность того, что среди этих400изделий окажется от34до50нестандартных?
Решение.
1. Наивероятнейшее числоk0событий в серии изnповторных независимых испытаний находим как целое число, заключённое в пределах:np – q k0 np + p.
В нашей задаче:
общее число испытаний n = 400(количество отобранных для контроля изделий);
p = (90%) = 0,9— вероятность того, что наугад выбранное изделие является стандартным;
q = 1 – p = 1 – 0,9 = 0,1— вероятность того, что наугад выбранное изделие является нестандартным.
Подставляем числовые данные в двойное неравенство, получим
400·0,9 – 0,1 k0 400·0,9 + 0,9 360 – 0,1 k0 360 + 0,9
359,9 k0 360,9.
В этих пределах находится единственное целое число k0=360, т.е. вероятнее всего, что из наугад выбранных400изделий стандартными окажутся360.
При больших значениях nнаивероятнейшее числоk0событий приближённо можно находить из соотношения
k0 n·p = 400·0,9 = 360.
2. Найдём вероятность P400(360), используя локальную формулу Лапласа:
![]() ,
,
где
![]() ,
а
,
а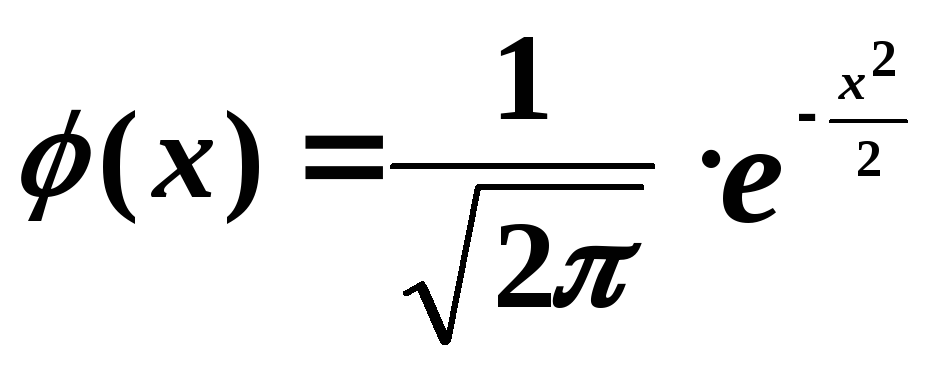 — нормированная функция Гаусса.
— нормированная функция Гаусса.
Тогда
![]() .
.
Для
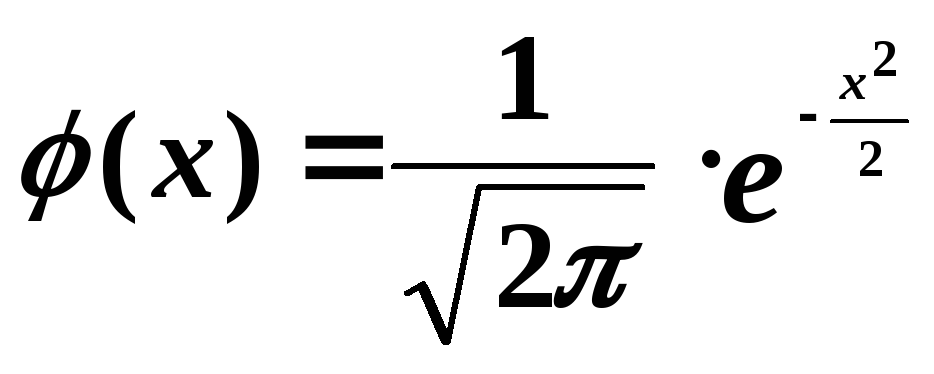 составлены таблицы в зависимости от её
аргумента
составлены таблицы в зависимости от её
аргумента
![]() .
.
Находим, что значение функции Гаусса
![]() .
Тогда искомая вероятность будет:
.
Тогда искомая вероятность будет:
![]() .
.
3. Вероятность P400 (34 k 50) того, что среди 400 изделий окажется от 34 до 50 нестандартных будем находить, используя интегральную теорему Лапласа:
Pn(k1kk2)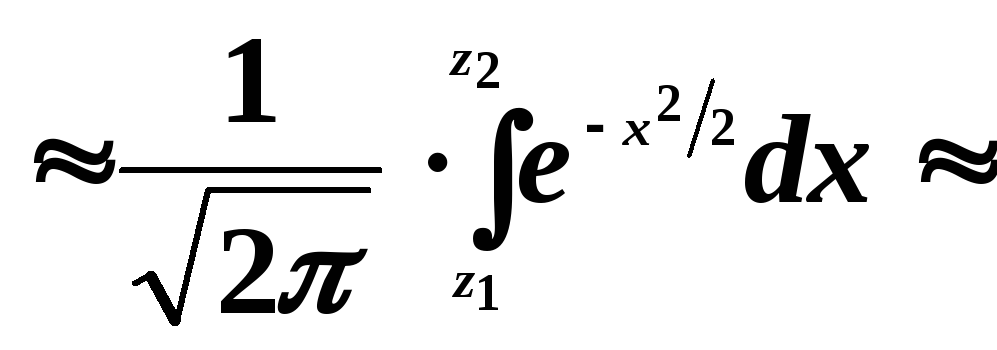 Ф(z2)
–Ф(z1),
Ф(z2)
–Ф(z1),
где
![]() — функция Лапласа, а
— функция Лапласа, а![]() ,
,![]() — её аргументы.
— её аргументы.
Но здесь следует изменить вероятности pиqпрямого и противоположного событий:
p— вероятность того, что наугад выбранное изделие является нестандартным,p = 0,1;
q — вероятность того, что наугад выбранное изделие является стандартным,q = 0,9.
Находим аргументы функции Лапласа:
![]()
![]()
Тогда Pn(k1 k k2) Ф(z2) – Ф(z1) = Ф(1,67) – Ф(-1).
Значения функции Лапласа находим в таблице, учитывая, что эта функция нечётная Ф(‑x) = ‑ Ф(x).
Тогда Ф(1,67) = 0,4525, Ф (-1) = -0,3413, получаем:
P400(34 k 50) Ф(z2) – Ф(z1) = Ф(1,67) – Ф(-1) = 0,4525 – (- 0,3413) = 0,4525 + 0,3413 = 0,7938.
Ответ.1. Вероятнее всего, что из400наугад выбранных для контроля изделий стандартными окажутсяk0=360шт.
2. Вероятность того, что из400наугад выбранных для контроля изделий стандартными окажутся360, —P400(360)0,06650,07.
3. Вероятность того, что из400наугад выбранных для контроля изделий нестандартными окажутся не менее34и не более50, будет равнаP400(34k50)0,79380,79.
Пример 6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величиныX, заданной функцией плотности:
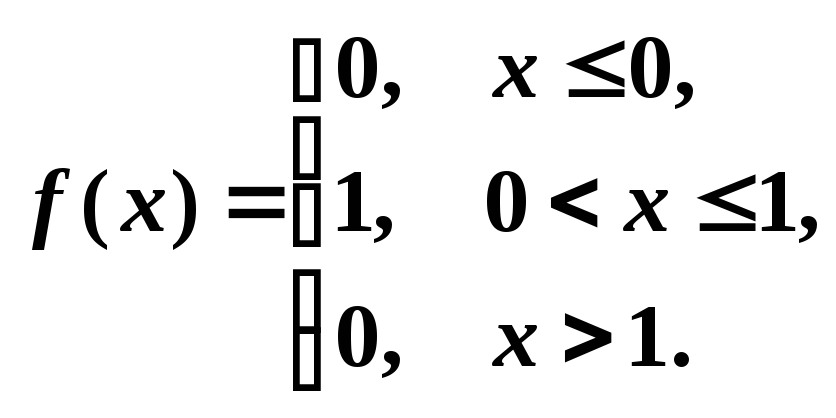
Решение. Математическое ожидание непрерывной случайной величины X, возможные значения которой принадлежат отрезку [a, b], вычисляется по формуле:
![]() .
.
Найдем
![]() :
:
![]() .
.
Дисперсия вычисляется по формуле:
![]() .
.
Среднее квадратическое отклонение находим по формуле:
![]() .
.
Ответ. Математическое ожидание
случайной величиныX
![]() ;
дисперсия
;
дисперсия![]() ;
среднее квадратическое отклонение —
;
среднее квадратическое отклонение —![]() .
.
Пример 7. Случайная величинаXподчинена закону распределения с плотностьюf(x), причемaнеизвестно:
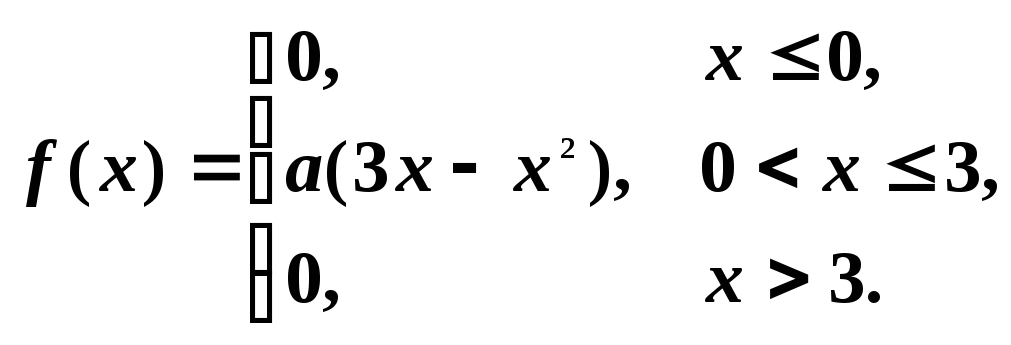
Требуется:
1. Найти коэффициент a.
2. Найти вероятность попадания Xв промежуток (1; 2).
Решение. 1. Так как все значения
данной случайной величины заключены
на отрезке [0; 3], то по формуле![]() ,
откуда
,
откуда
![]() или
или![]() ,следовательно,
,следовательно,
![]() .
.
Таким образом, плотность распределения имеет вид:
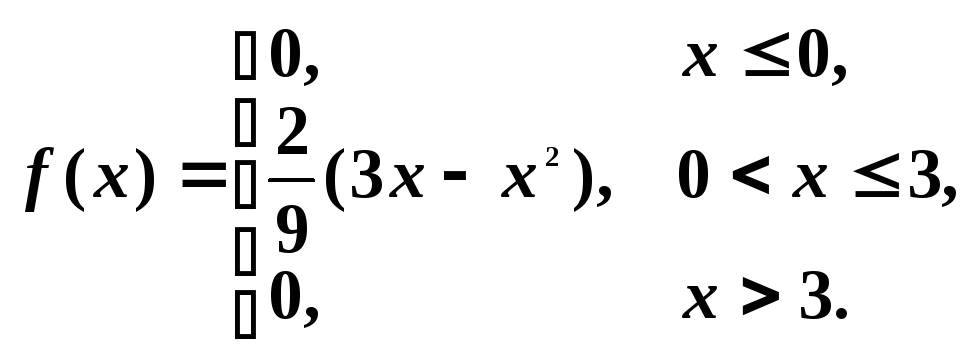
2. Вероятность попадания случайной
величины Xв промежуток (1; 2) найдем
по формуле (2.33), учитывая, что![]() на промежутке (1; 2):
на промежутке (1; 2):
![]()
Ответ.![]() ,
,![]() .
.
Пример 8. Случайная величина распределена нормально с параметрами a = 8, = 3. Найти вероятность того, что случайная величина в результате опыта примет значение, заключенное в интервале (12,5;14).
Решение. Воспользуемся формулой:![]() .
.
Так как = 12,5,= 14,a = 8,= 3, имеем![]() .
.
Тогда P(12,5 < x < 14) = Ф(2) – Ф(1,5) = 0,4772 – 0,4332 = 0,0440.
Ответ.Вероятность того, что случайная величина примет значение, заключенное в интервале (12,5; 14), равна 0,0440.
