
- •Фгоу впо «Волгоградская академия государственной службы»
- •1.2. Цели и задачи учебной дисциплины.
- •1.3. Требования к уровню освоения дисциплины (знания, умения, навыки).
- •1.4. Тематический план курса «математика» (174 ч.)
- •1.5. Учебно-методическое обеспечение учебной дисциплины
- •Тема 6. Понятие функции. Способы задания и основные свойства функций.
- •Тема 7. Предел последовательности и функции. Правила вычисления пределов.
- •Тема 8. Замечательные пределы. Непрерывность функции. Основные теоремы о непрерывных функциях. Точки разрыва и их классификация.
- •Тема 9. Задачи, приводящие к производной. Понятие производной функции.
- •Тема 10. Производная неявных и параметрических функций. Производные высших порядков.
- •Тема 11. Понятие дифференциала функции.
- •Тема 12. Основные теоремы о дифференцируемых функциях. Теоремы Ферма, Ролля, Лагранжа и Коши. Правило Лопиталя-Бернулли раскрытия неопределенностей вида и.
- •Тема 13. Полное исследование функций и построение графиков.
- •Тема 14. Первообразная и неопределенный интеграл. Свойства интеграла. Таблица неопределенных интегралов.
- •Тема 15. Основные методы интегрирования.
- •Тема 16. Понятие определенного интеграла. Свойства и правила вычисления определенного интеграла.
- •Тема 17. Приложения определенного интеграла. Несобственные интегралы.
- •Планы семинарских и практических занятий
- •Тема 1. Операции над матрицами. Определители третьего порядка. (2 часа)
- •Тема 2. Определители четвертого и выше порядков. Элементарные преобразования определителей. Обратная матрица. (4 часа)
- •Тема 3. Ранг матрицы.(4 часа)
- •Тема 8. Замечательные пределы. Основные эквивалентные функции (4 часа).
- •Тема 9. Определение производной. Геометрический смысл. Основные правила дифференцирования. Таблица производных элементарных функций.(2 часа)
- •Тема 10. Производные неявных и параметрических функций. Логарифмическое дифференцирование. Производные высших порядков.(2 часа)
- •Тема 11. Дифференциал функции. Приложение производной в теории пределов. (2 часа)
- •Тема 12. Общая схема исследования функций и построения их графиков.(2 часа)
- •Тема 13. Контрольная работа.(2 часа)
- •Тема 14. Неопределенный интеграл. Свойства неопределенного интеграла. Интегралы от основных элементарных функций. Основные методы интегрирования.(2 часа)
- •Тема 15. Основные методы интегрирования: интегрирование по частям.(2 часа)
- •Тема 16. Определенный интеграл. Формула Ньютона-Лейбница. Методы интегрирования. Геометрические приложения определенного интеграла. (4 часа)
- •Темы, выносимые на самостоятельное изучение:
- •Тема 1. Основы теории множеств.
- •Тема 2. Элементы аналитической геометрии.
- •Вопросы к зачету:
- •Материалы текущего, промежуточного и итогового контроля Вопросы к аттестации
- •Контрольная работа № 1
- •Тема 19. Экстремум функций нескольких переменных. Наибольшее и наименьшее значения функции. Условный экстремум.
- •Тема 20. Условный экстремум функций нескольких переменных.
- •Тема 21. Основные понятия теории дифференциальных уравнений. Дифференциальные уравнения первого порядка.
- •Тема 22. Линейные неоднородные дифференциальные уравнения первого порядка.
- •Тема 23. Линейные однородные дифференциальные уравнения второго порядка. Линейные неоднородные дифференциальные уравнения второго порядка с правой частью специального вида.
- •Тема 24. Линейные неоднородные дифференциальные уравнения второго порядка. Метод Лагранжа.
- •Тема 30. Алгебра событий. Теоремы сложения и умножения вероятностей событий.
- •Тема 31. Формула полной вероятности. Формула Байеса.
- •Планы семинарских и практических занятий
- •Тема 1. Функции нескольких переменных. Частные производные. Дифференциал. (4 часа)
- •Тема 2. Экстремум функций двух переменных. Наибольшее и наименьшее значения функции. (2 часа)
- •Тема 3. Дифференциальные уравнения. Общее решение дифференциального уравнения. Задача Коши. (2 часа)
- •Тема 4. Линейные неоднородные дифференциальные уравнения первого порядка. (2 часа)
- •Тема 5. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Уравнения однородные. Неоднородные уравнения с правой частью специального вида. (4 часа)
- •Тема 6. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод Лагранжа. (4 часа)
- •Тема 7. Числовые ряды. Определение сходимости ряда. Основные свойства рядов. Необходимый признак сходимости числового ряда.Достаточные признаки сходимости знакоположительных рядов. (4 часа)
- •Тема 8. Знакочередующиеся ряды. Теорема Лейбница.(2 часа)
- •Тема 9. Понятие функционального ряда. Область сходимости. Степенной ряд. Интервал и радиус сходимости степенного ряда.(2 часа)
- •Тема 10. Разложение функций в степенные ряды. Формула и ряд Тейлора. Формула и ряд Маклорена. Применение рядов в приближенных вычислениях. (2 часа)
- •Тема 11. Контрольная работа. (2 часа)
- •Тема 12. Классическое определение вероятности. Элементы комбинаторики. Алгебра событий. Теоремы сложения и умножения вероятностей. (2 часа)
- •Тема 13. Формула полной вероятности. Формула Байеса. (2 часа)
- •Тема 14. Последовательность независимых испытаний. Наивероятнейшее число появлений события в серии из n независимых испытаний. Асимптотические формулы.(2 часа)
- •Тема 15. Контрольная работа.(2 часа)
- •Тема 16. Дискретная и непрерывная случайная величина. Закон распределения. Числовые характеристики.(2 часа)
- •Тема 17. Классические законы распределения случайных величин. Биномиальный закон. Равномерное и показательное распределение. Нормальная случайная величина.(2 часа)
- •Темы, выносимые на самостоятельное изучение:
- •Тема 1. Самостоятельное решение задач по теории дифференциальных уравнений и теории рядов.
- •Тема 2. Самостоятельное решение задач по теории вероятностей.
- •Вопросы к экзамену:
- •Материалы текущего, промежуточного и итогового контроля Вопросы к аттестации
- •Контрольная работа № 1 Примерный вариант заданий
- •Контрольная работа № 2 Примерный вариант заданий
- •Примерный вариант экзаменационного билета
- •Список рекомендуемой литературы
- •Раздел 2. Методические рекомендации по изучению учебной дисциплины для студентов
- •2.1. Рекомендации по использованию материалов учебно-методического комплекса:
- •2.2. Пожелания к изучению отдельных тем курса
- •2. 3. Рекомендации по работе с литературой
- •2.4. Советы по подготовке к экзамену (зачету)
- •Раздел 3. Материалы тестовой системы или практикум по решению задач по темам лекций
- •Iсеместр
- •Примеры решения задач по темам 1 – 5
- •Примерный вариант практического задания по Темам 1 – 5.
- •Примеры решения задач по темам 6 – 13
- •Примерный вариант практического задания по Темам 6 – 13.
- •Примеры решения задач по темам 14 – 17
- •Примерный вариант практического задания по Темам 14 – 17.
- •IIсеместр
- •Примеры решения задач по темам 18 – 24
- •Примерный вариант практического задания по Темам 18 – 24.
- •Примеры решения задач по темам 25 – 28
- •Примерный вариант практического задания по Темам 25 – 28.
- •Примеры решения задач по темам 29 – 35
- •Примерный вариант практического задания по Темам 29 – 35.
- •Раздел 4. Словарь основных терминов (глоссарий)
Примерный вариант практического задания по Темам 1 – 5.
1. Найти матрицу, обратную матрице A. Проверить результат, вычислив произведение данной и обратной матриц.
A=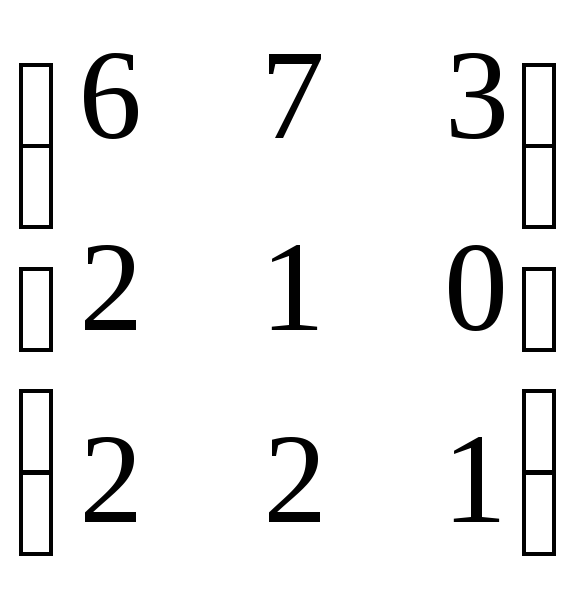
2. Решить систему уравнений двумя способами: матричным методом и по формулам Крамера:
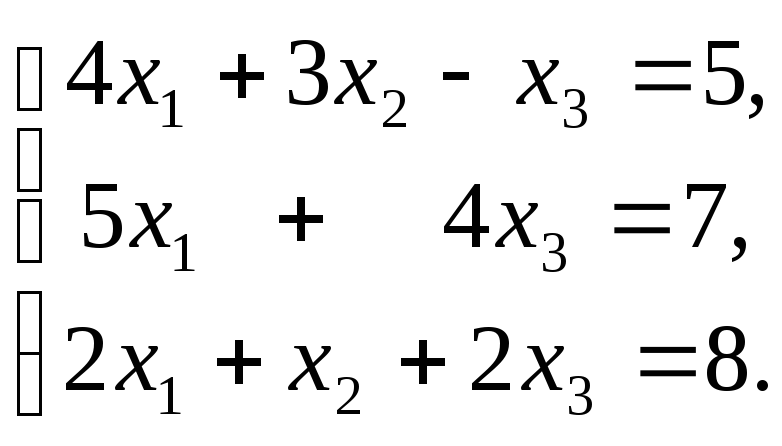
3. Фирма производит оплату трем категориям K1,K2,K3своих служащих по трем видам начислений:N1– должностной оклад,N2– надбавка за стаж работы в фирме иN3– премиальные выплаты. Нормы выплат и объем расхода денежных средств на один день заданы таблицей. Найти количество работников каждой из категорий, которые могут работать в ней при таких исходных данных.
|
Виды начислений |
Нормы выплат по категориям (ден. ед.) |
Объем расхода денежных средств на 1 день (ден. ед.) | ||
|
K1 |
K2 |
K3 | ||
|
N1 |
7 |
3 |
4 |
280 |
|
N2 |
6 |
2 |
3 |
230 |
|
N3 |
5 |
9 |
1 |
250 |
4. Построить множество решений системы линейных неравенств и найти координаты его угловых точек.
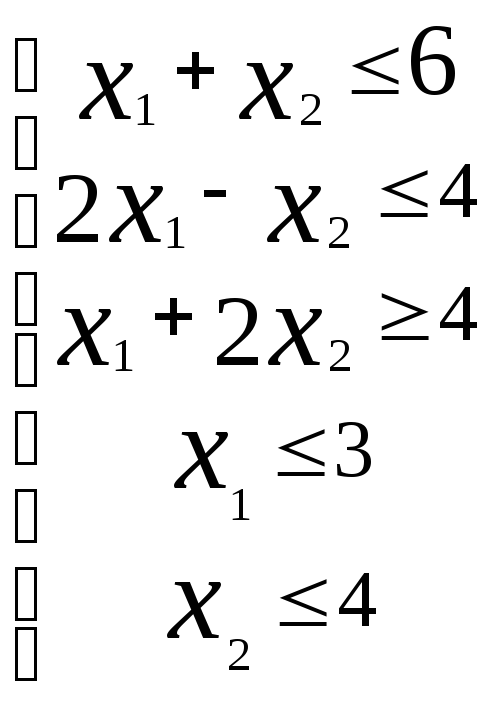
5. Определить, являются ли матрица AиBособенными, и перемножитьAнаBиBнаA:
A =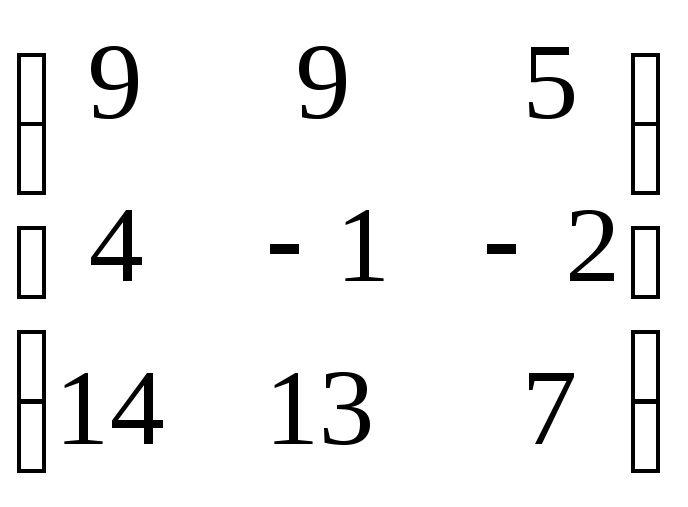 B =
B =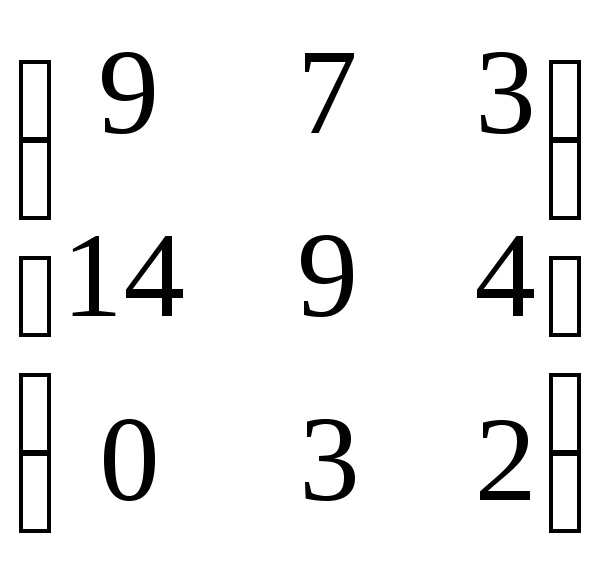
6. Решить систему линейных алгебраических уравнений методом Гаусса и выполнить проверку.
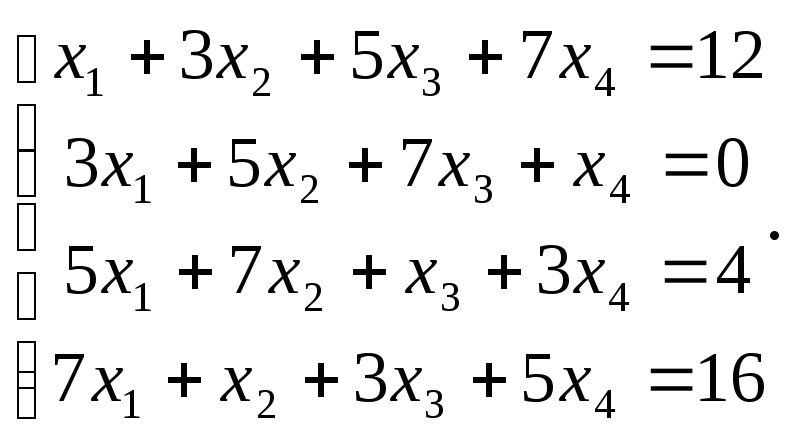
Примеры решения задач по темам 6 – 13
Пример
1.
![]() .
.
Решение. Подстановка предельного значения x= 2, дает нам неопределенность вида 0/0. Избавимся от нее путем разложения числителя и знаменателя на линейные множители.
2x2
– 3x
– 2 = 0 —
квадратный трехчлен, корни которого
находим по формулам корней
квадратного уравнения:
![]() ,
т. е.
,
т. е.![]() .
Итак,
.
Итак,![]() ,x2 =
2. Зная корни,
имеем разложение трехчлена: ax2
+ bx
+ c
= a(x
– x1)(x
– x2)
или, в нашем
случае,
,x2 =
2. Зная корни,
имеем разложение трехчлена: ax2
+ bx
+ c
= a(x
– x1)(x
– x2)
или, в нашем
случае,
![]() .
.
Аналогично получаем для знаменателя x2 – 2x = x(x – 2). Тогда наш предел примет вид:
![]() .
.
Теперь подставим под знак предела значение x = 2:
![]() .
.
Пример
2.
![]() .
.
Решение.
Подстановка предельного значения x
= –1
дает неопределенность вида 0/0.
Избавимся от нее, умножая числитель и
знаменатель на выражение, сопряженное
знаменателю,
т.е. на
![]() ;
тогда имеем:
;
тогда имеем:
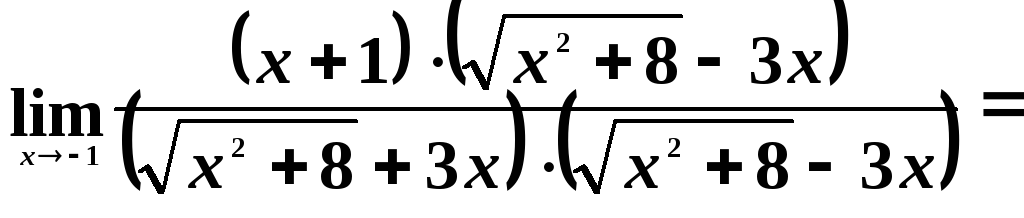
![]() .
.
В знаменателе выносим общий множитель, раскладываем разность квадратов и получаем
![]()
![]()
![]() .
.
Пример
3.
![]() .
.
Решение. Имеем неопределенность вида /. Разделим числитель и знаменатель дроби на старшую степень x, т.е. на x3:
![]()
(т.к. выражения 7/x, 2/x3, 4/x2, 3/x3 при x имеют своим пределом 0).
Пример
4.
![]() .
.
Решение.
Выделяем в круглых скобках единицу, для
чего делаем следующие преобразования:![]() .
.
Теперь воспользуемся вторым замечательным пределом:
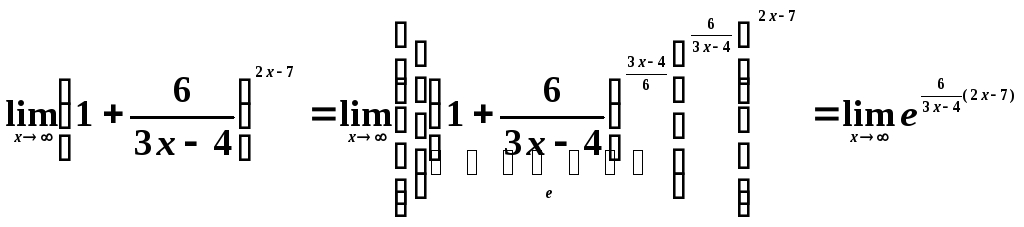 .
.
Предел в показателе степени вычислим как предел отношения многочленов:
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Пример
5.
![]() .
.
Решение.
Числитель запишем в виде
![]() ,
а знаменатель — в виде
,
а знаменатель — в виде![]() .
Используя соотношение
.
Используя соотношение![]() ,
при
,
при![]() получаем:
получаем:
![]()
![]() ,
,
![]()
![]() .
.
Значит,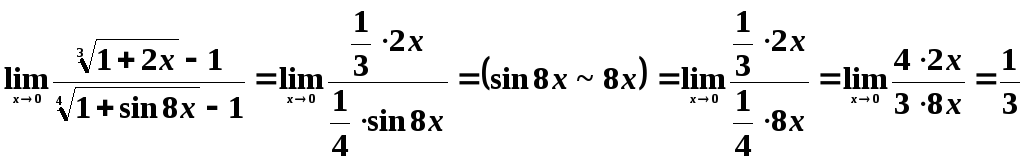 .
.
Пример
6. Найти
![]() ,
где
,
где![]() [1].
[1].
Решение. Функция y — четная, поэтому будем считать x > 0. Тогда
![]() .
Теперь вычислим
.
Теперь вычислим
![]() :
:
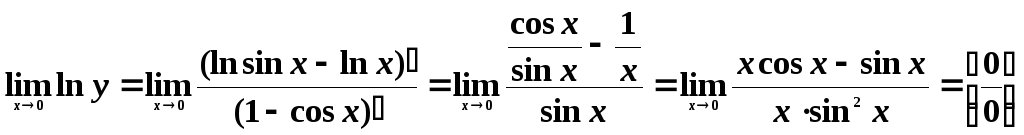 =
=
![]() .
.
Сократим
полученную дробь на x
sinx:
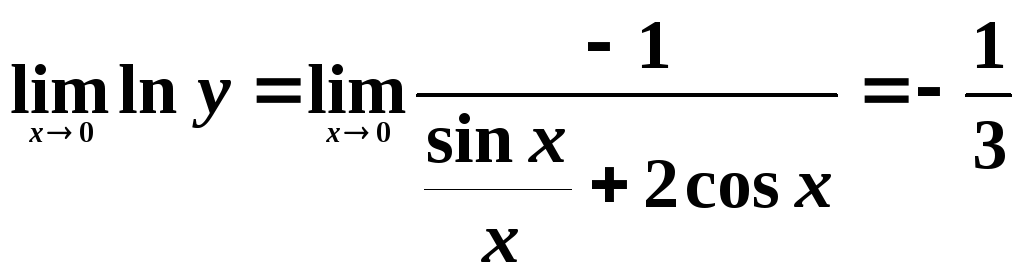 .
.
Таким
образом,
![]() .
.
Пример
7. Исследовать
на непрерывность функцию
![]() .
.
Решение.
Выражение
![]() не определено приx
=
0,
следовательно, точка x
=
0
есть точка разрыва заданной функции.
Определим вид разрыва.
не определено приx
=
0,
следовательно, точка x
=
0
есть точка разрыва заданной функции.
Определим вид разрыва.
Выполним
замену переменной
![]() ,
тогда приx
0
t
и
,
тогда приx
0
t
и
![]() .
.
Таким образом, при x = 0 имеем разрыв первого рода, а именно — скачок.
Пример
8. Исследовать
функцию
![]() и построить ее график.
и построить ее график.
Решение.
1. Найдем область определения функции, интервалы непрерывности, точки разрыва.
Сначала найдем область определения заданной функции. Для этого представим ее в виде:
![]() .
.
В числителе этой дроби стоит многочлен, непрерывный на всей числовой оси, а знаменатель обращается в нуль в точке x = 0. Итак, областью определения данной функции являются две полуоси – < x < 0 и 0 < x < +, т.е. D(f) = (–; 0) (0; +),
в этих двух интервалах функция будет непрерывна.
2. Найдем точки пересечения графика функции с осями координат.
Так как точка x = 0 не входит в область определения функции, то точек пересечения графика с осью ординат Oy нет. График функции пересекается с осью абсцисс Ox, если y = 0, т.е.
![]() ,
,
причем x 0, т.е. знаменатель дроби в нуль никогда не обращается. Тогда дробь равна нулю, если ее числитель равен нулю: 3x2 – 5x – 2 = 0. Ищем корни квадратного уравнения:
Получаем
![]() .
Итак, график функции имеет две точки
пересечения с осьюOx:
.
Итак, график функции имеет две точки
пересечения с осьюOx:
![]() и
и![]() .
.
3. Исследуем данную функцию на четность и нечетность.
Функция
является четной, если выполняется
равенство f(x)
= f(–x).
Функция является нечетной, если f(x)
= –f(–x).
Заданная функция
![]() .
Найдемf(–x):
.
Найдемf(–x):
![]() .
.
Несложно видеть, что f(x) f(–x) и f(x) –f(–x), т.е. данная функция не является ни четной, ни нечетной.
4. Найдем асимптоты графика функции.
а) Вертикальные асимптоты могут быть только в точках разрыва графика функции. В нашем случае это точка x = 0. Найдем пределы слева и справа заданной функции в этой точке:
![]() ,
,
![]() ,
,
Итак, оба односторонних предела равны –, поэтому прямая x = 0 является вертикальной асимптотой.
б)
У графика функции есть горизонтальная
асимптота y
= b,
если существует конечный предел
![]() (или конечный предел существует только
приx
–
или только при x +).Так как
(или конечный предел существует только
приx
–
или только при x +).Так как
![]() ,
то прямаяy
= 3 является
горизонтальной асимптотой. Так как эта
прямая является двусторонней горизонтальной
асимптотой (т.е. при x
),
то наклонных асимптот у графика функции
нет.
,
то прямаяy
= 3 является
горизонтальной асимптотой. Так как эта
прямая является двусторонней горизонтальной
асимптотой (т.е. при x
),
то наклонных асимптот у графика функции
нет.
Итак, у графика заданной функции есть вертикальная асимптота x = 0 и горизонтальная асимптота y = 3.
5. Теперь перейдем к отысканию интервалов возрастания и убывания функции и точек ее экстремума.
Найдем производную:
![]() =
=![]() .
.
а)
Функция возрастает, если y'
> 0. Мы имеем
неравенство
![]() .
Как известно, дробь является положительной,
если числитель и знаменатель имеют
одинаковые знаки. Тогда наше неравенство
распадется на две системы неравенств:
.
Как известно, дробь является положительной,
если числитель и знаменатель имеют
одинаковые знаки. Тогда наше неравенство
распадется на две системы неравенств:
|
|
и |
|
Решаем эти системы:
|
|
|
Объединяя эти два результата, получаем область возрастания заданной функции:
(–;–4/5)(0; +).
б)
Аналогично, из условия y'
< 0 (в нашем
случае —
![]() ),
получим область убывания функции. Дробь
меньше нуля, если ее числитель и
знаменатель имеют разные знаки. Тогда
полученное неравенство распадется на
следующие две системы неравенств:
),
получим область убывания функции. Дробь
меньше нуля, если ее числитель и
знаменатель имеют разные знаки. Тогда
полученное неравенство распадется на
следующие две системы неравенств:
|
|
и |
|
Решаем эти системы:
|
|
|
Объединяя
эти два результата, получаем область
убывания заданной функции:
![]() .
.
в)
Из условия y'
= 0, определим
критические точки заданной функции.
Решим уравнение
![]() .
Так какx
0, то 5x
+ 4 = 0,
откуда
.
Так какx
0, то 5x
+ 4 = 0,
откуда
![]() .
Это — критическая точка. Выше определили,
что слева от этой точки, в интервале
(–;
–4/5)
первая производная положительна и
функция возрастает, а справа, в интервале
.
Это — критическая точка. Выше определили,
что слева от этой точки, в интервале
(–;
–4/5)
первая производная положительна и
функция возрастает, а справа, в интервале
![]() ,
первая производная отрицательна, и
функция, соответственно, убывает. При
переходе через критическую точку
,
первая производная отрицательна, и
функция, соответственно, убывает. При
переходе через критическую точку![]() происходит смена знака производной с
плюса на минус, следовательно,
точка
происходит смена знака производной с
плюса на минус, следовательно,
точка
![]() является точкой максимума заданной
функции. Значение функции в этой точке
является точкой максимума заданной
функции. Значение функции в этой точке![]() .
.
Итак,
точка
![]() является точкой максимума данной
функции.
является точкой максимума данной
функции.
6. Найдём теперь интервалы выпуклости и точки перегиба графика заданной функции.
Интервалы выпуклости определим по знаку второй производной. Найдем ее, продифференцировав первую производную:
![]() ,
,
![]() .
.
Так как знаменатель полученной дроби x4 всегда положителен (за исключением значения x 0), то знак производной определяется знаком числителя – (10x + 12).
а)
Функция будет выпуклой вверх на
промежутке, где y''
< 0. Решением
неравенства – (10x
+ 12) < 0
или 10x
+ 12 > 0
является интервал
![]() .
Исключая значениеx
0, получаем,
что на интервале
.
Исключая значениеx
0, получаем,
что на интервале
![]() график функции будет выпуклым вверх.
график функции будет выпуклым вверх.
б)
Аналогично, из условия y''
> 0 (в нашем
случае, –(10x
+12) > 0)
определим интервал, на котором функция
будет выпукла вниз. Решая последнее
неравенство, определяем интервал
![]() или
или![]() ,
на котором график функции будет выпуклым
вниз.
,
на котором график функции будет выпуклым
вниз.
в)
Необходимым условием существования
точки перегиба является равенство нулю
второй производной (y''
= 0), что для
нашей функции имеет место при
![]() .
.
Достаточным
условием наличия точки перегиба служит
смена знака второй производной при
переходе через эту точку. У нас это
условие выполнено, следовательно,
![]() — точка перегиба графика заданной
функции. Значение функции в этой точке
— точка перегиба графика заданной
функции. Значение функции в этой точке![]() .
Итак, точка
.
Итак, точка![]() есть точка перегиба графика заданной
функции.
есть точка перегиба графика заданной
функции.
7. Составляем сводную таблицу.
|
x |
|
|
|
|
|
0 |
(0; +) |
|
f(x) |
|
|
|
|
|
разрыв |
|
|
f'(x) |
+ |
0, макс. |
– |
+ | |||
|
f''(x) |
+ |
0, перегиб |
– |
– | |||
8. По результатам исследования функции строим график.
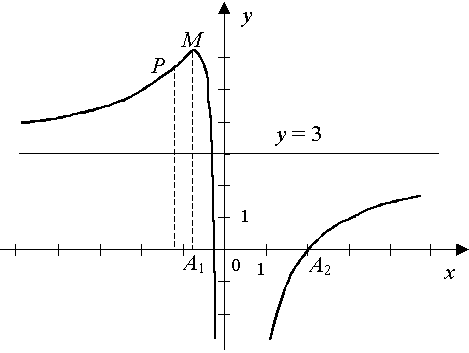

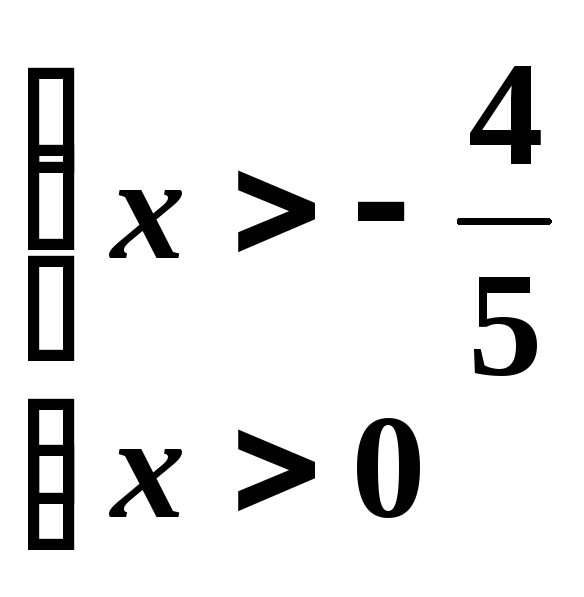 ,
откуда x
> 0.
,
откуда x
> 0.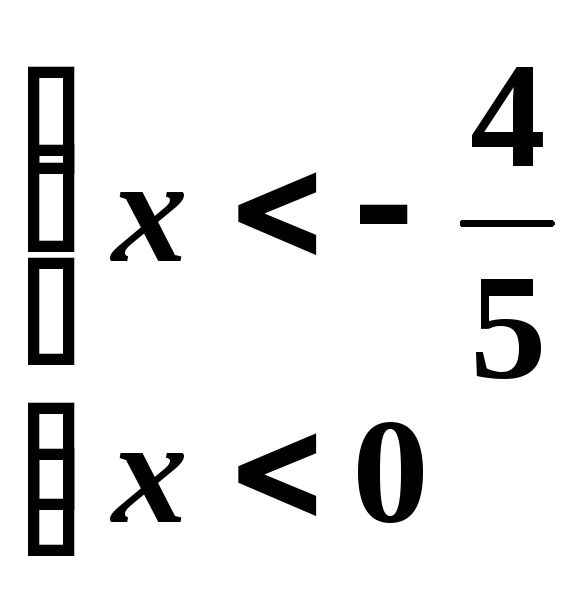 ,
откуда
,
откуда
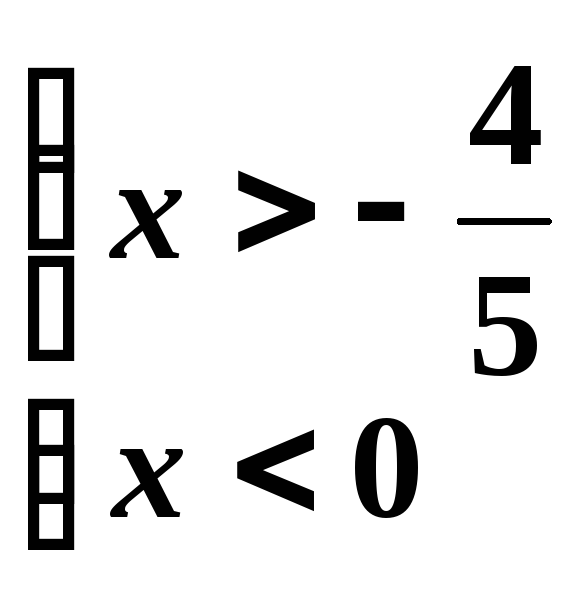 ,
откуда
,
откуда
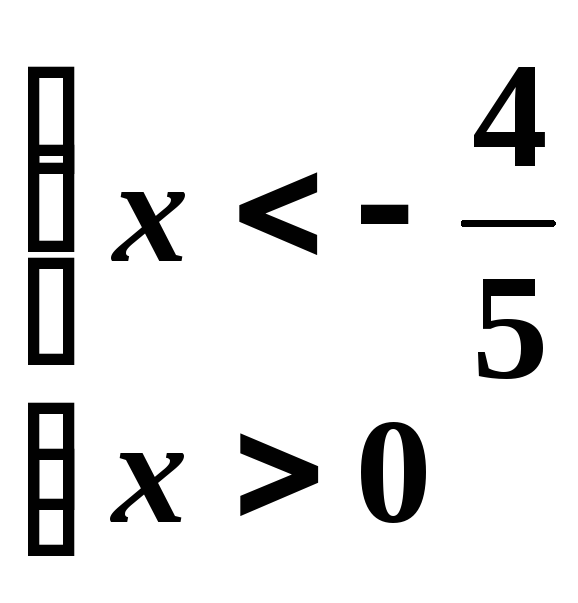 —эта
система несовместна.
—эта
система несовместна.