
- •Фгоу впо «Волгоградская академия государственной службы»
- •1.2. Цели и задачи учебной дисциплины.
- •1.3. Требования к уровню освоения дисциплины (знания, умения, навыки).
- •1.4. Тематический план курса «математика» (174 ч.)
- •1.5. Учебно-методическое обеспечение учебной дисциплины
- •Тема 6. Понятие функции. Способы задания и основные свойства функций.
- •Тема 7. Предел последовательности и функции. Правила вычисления пределов.
- •Тема 8. Замечательные пределы. Непрерывность функции. Основные теоремы о непрерывных функциях. Точки разрыва и их классификация.
- •Тема 9. Задачи, приводящие к производной. Понятие производной функции.
- •Тема 10. Производная неявных и параметрических функций. Производные высших порядков.
- •Тема 11. Понятие дифференциала функции.
- •Тема 12. Основные теоремы о дифференцируемых функциях. Теоремы Ферма, Ролля, Лагранжа и Коши. Правило Лопиталя-Бернулли раскрытия неопределенностей вида и.
- •Тема 13. Полное исследование функций и построение графиков.
- •Тема 14. Первообразная и неопределенный интеграл. Свойства интеграла. Таблица неопределенных интегралов.
- •Тема 15. Основные методы интегрирования.
- •Тема 16. Понятие определенного интеграла. Свойства и правила вычисления определенного интеграла.
- •Тема 17. Приложения определенного интеграла. Несобственные интегралы.
- •Планы семинарских и практических занятий
- •Тема 1. Операции над матрицами. Определители третьего порядка. (2 часа)
- •Тема 2. Определители четвертого и выше порядков. Элементарные преобразования определителей. Обратная матрица. (4 часа)
- •Тема 3. Ранг матрицы.(4 часа)
- •Тема 8. Замечательные пределы. Основные эквивалентные функции (4 часа).
- •Тема 9. Определение производной. Геометрический смысл. Основные правила дифференцирования. Таблица производных элементарных функций.(2 часа)
- •Тема 10. Производные неявных и параметрических функций. Логарифмическое дифференцирование. Производные высших порядков.(2 часа)
- •Тема 11. Дифференциал функции. Приложение производной в теории пределов. (2 часа)
- •Тема 12. Общая схема исследования функций и построения их графиков.(2 часа)
- •Тема 13. Контрольная работа.(2 часа)
- •Тема 14. Неопределенный интеграл. Свойства неопределенного интеграла. Интегралы от основных элементарных функций. Основные методы интегрирования.(2 часа)
- •Тема 15. Основные методы интегрирования: интегрирование по частям.(2 часа)
- •Тема 16. Определенный интеграл. Формула Ньютона-Лейбница. Методы интегрирования. Геометрические приложения определенного интеграла. (4 часа)
- •Темы, выносимые на самостоятельное изучение:
- •Тема 1. Основы теории множеств.
- •Тема 2. Элементы аналитической геометрии.
- •Вопросы к зачету:
- •Материалы текущего, промежуточного и итогового контроля Вопросы к аттестации
- •Контрольная работа № 1
- •Тема 19. Экстремум функций нескольких переменных. Наибольшее и наименьшее значения функции. Условный экстремум.
- •Тема 20. Условный экстремум функций нескольких переменных.
- •Тема 21. Основные понятия теории дифференциальных уравнений. Дифференциальные уравнения первого порядка.
- •Тема 22. Линейные неоднородные дифференциальные уравнения первого порядка.
- •Тема 23. Линейные однородные дифференциальные уравнения второго порядка. Линейные неоднородные дифференциальные уравнения второго порядка с правой частью специального вида.
- •Тема 24. Линейные неоднородные дифференциальные уравнения второго порядка. Метод Лагранжа.
- •Тема 30. Алгебра событий. Теоремы сложения и умножения вероятностей событий.
- •Тема 31. Формула полной вероятности. Формула Байеса.
- •Планы семинарских и практических занятий
- •Тема 1. Функции нескольких переменных. Частные производные. Дифференциал. (4 часа)
- •Тема 2. Экстремум функций двух переменных. Наибольшее и наименьшее значения функции. (2 часа)
- •Тема 3. Дифференциальные уравнения. Общее решение дифференциального уравнения. Задача Коши. (2 часа)
- •Тема 4. Линейные неоднородные дифференциальные уравнения первого порядка. (2 часа)
- •Тема 5. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Уравнения однородные. Неоднородные уравнения с правой частью специального вида. (4 часа)
- •Тема 6. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод Лагранжа. (4 часа)
- •Тема 7. Числовые ряды. Определение сходимости ряда. Основные свойства рядов. Необходимый признак сходимости числового ряда.Достаточные признаки сходимости знакоположительных рядов. (4 часа)
- •Тема 8. Знакочередующиеся ряды. Теорема Лейбница.(2 часа)
- •Тема 9. Понятие функционального ряда. Область сходимости. Степенной ряд. Интервал и радиус сходимости степенного ряда.(2 часа)
- •Тема 10. Разложение функций в степенные ряды. Формула и ряд Тейлора. Формула и ряд Маклорена. Применение рядов в приближенных вычислениях. (2 часа)
- •Тема 11. Контрольная работа. (2 часа)
- •Тема 12. Классическое определение вероятности. Элементы комбинаторики. Алгебра событий. Теоремы сложения и умножения вероятностей. (2 часа)
- •Тема 13. Формула полной вероятности. Формула Байеса. (2 часа)
- •Тема 14. Последовательность независимых испытаний. Наивероятнейшее число появлений события в серии из n независимых испытаний. Асимптотические формулы.(2 часа)
- •Тема 15. Контрольная работа.(2 часа)
- •Тема 16. Дискретная и непрерывная случайная величина. Закон распределения. Числовые характеристики.(2 часа)
- •Тема 17. Классические законы распределения случайных величин. Биномиальный закон. Равномерное и показательное распределение. Нормальная случайная величина.(2 часа)
- •Темы, выносимые на самостоятельное изучение:
- •Тема 1. Самостоятельное решение задач по теории дифференциальных уравнений и теории рядов.
- •Тема 2. Самостоятельное решение задач по теории вероятностей.
- •Вопросы к экзамену:
- •Материалы текущего, промежуточного и итогового контроля Вопросы к аттестации
- •Контрольная работа № 1 Примерный вариант заданий
- •Контрольная работа № 2 Примерный вариант заданий
- •Примерный вариант экзаменационного билета
- •Список рекомендуемой литературы
- •Раздел 2. Методические рекомендации по изучению учебной дисциплины для студентов
- •2.1. Рекомендации по использованию материалов учебно-методического комплекса:
- •2.2. Пожелания к изучению отдельных тем курса
- •2. 3. Рекомендации по работе с литературой
- •2.4. Советы по подготовке к экзамену (зачету)
- •Раздел 3. Материалы тестовой системы или практикум по решению задач по темам лекций
- •Iсеместр
- •Примеры решения задач по темам 1 – 5
- •Примерный вариант практического задания по Темам 1 – 5.
- •Примеры решения задач по темам 6 – 13
- •Примерный вариант практического задания по Темам 6 – 13.
- •Примеры решения задач по темам 14 – 17
- •Примерный вариант практического задания по Темам 14 – 17.
- •IIсеместр
- •Примеры решения задач по темам 18 – 24
- •Примерный вариант практического задания по Темам 18 – 24.
- •Примеры решения задач по темам 25 – 28
- •Примерный вариант практического задания по Темам 25 – 28.
- •Примеры решения задач по темам 29 – 35
- •Примерный вариант практического задания по Темам 29 – 35.
- •Раздел 4. Словарь основных терминов (глоссарий)
Планы семинарских и практических занятий
Тема 1. Функции нескольких переменных. Частные производные. Дифференциал. (4 часа)
Рассматриваемые вопросы:
Частные производные.
Дифференцирование неявных функций. Полная производная.
Дифференциал функции двух переменных. Приложение дифференциала в приближенных вычислениях.
Задания для самостоятельного выполнения:
1. Найти частные производные до второго порядка включительно:
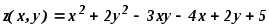
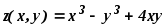
 ,
приx=1 и y=2
,
приx=1 и y=2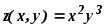
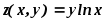
2. Найти частные производные в указанной точке:
2.1. ![]() , приx=3, y=4
, приx=3, y=4
2.2. ![]() , приx=2, y=4
, приx=2, y=4
2.3. ![]() , приx=1, y=1
, приx=1, y=1
3. Вычислить приближенно, применив линеаризацию функций двух переменных:
![]()
Тема 2. Экстремум функций двух переменных. Наибольшее и наименьшее значения функции. (2 часа)
Рассматриваемые вопросы:
Необходимое и достаточное условие экстремума функции двух переменных.
Исследование функции двух переменных на набольшее и наименьшее значения в замкнутой области..
Условный экстремум. Метод множителей Лагранжа. Сведение к задаче на экстремум функции одной переменной в случае линейного уравнения связи.
Задания для самостоятельного выполнения:
1. Исследовать на экстремум функции двух переменных, используя следующий
|
|
|
|
|
|
|
|
|
|
Тема 3. Дифференциальные уравнения. Общее решение дифференциального уравнения. Задача Коши. (2 часа)
Рассматриваемые вопросы:
Дифференциальные уравнения. Общее и частное решения. Геометрический смысл. Общий интеграл.
Задача Коши. Теорема существования и единственности решения задачи Коши.
Дифференциальные уравнения с разделенными переменными.
Интегрируемость дифференциальных уравнений первого порядка, разрешенных относительно производной, с правой частью – однородной функцией нулевого порядка.
Задания для самостоятельного выполнения:
1. Проинтегрировать дифференциальные уравнения с разделяющимися переменными:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Дифф. ур. первого порядка с правой частью однородной функцией нулевого порядка.
|
1)
|
4)
|
|
2)
|
5)
|
|
3) (x + y)dx + xdy = 0. |
6) (7x2 – 2xy + 6y2)dx + (x2 – 4xy)dy = 0. |
Тема 4. Линейные неоднородные дифференциальные уравнения первого порядка. (2 часа)
Рассматриваемые вопросы:
Линейные неоднородные дифференциальные уравнения 1 – го порядка. Метод Бернулли. Метод Лагранжа вариации произвольной постоянной. Структура общего решения.
Уравнение Бернулли.
Задания для самостоятельного выполнения:
1. Проинтегрировать линейные дифференциальные уравнения первого порядка:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Решить уравнения Бернулли.
|
|
|
|
|
|
|
|
|
|
|
