
Kluwer - Handbook of Biomedical Image Analysis Vol
.1.pdf
Improving the Initialization, Convergence, and Memory Utilization |
375 |
Figure 7.6: Original image with the outlined initial contour.
The obtained contour was plotted over the original image for matching (Fig. 7.6). If compared with Fig. 7.4(b) we observe an improvement in the obtained initialization.
7.3.3 Neural Nets
Neural networks have been used for instantiating deformable models for face detection [54] and handwritten digit recognition tasks [74] (see also [14] and references therein). To the best of our knowledge, there are no references using neural nets to initialize deformable models for medical images. However, the network system proposed in [25], which segments MR images of the thorax, may be closer to this proposal.
In this method each slice is a gray-level image composed of (256 × 256) pixels values and is accompanied by a corresponding (target) image containing just the outline of the region. Target images were obtained using a semiautomatic technique based on a region growing algorithm. The general idea is to use a multilayer perceptron (MLP), where each pixel of each slice is classified into a contour-boundary and non-contour-boundary one.
The inputs to the MLP are intensity values of pixels from a (7 × 7) window centered on the pixel to be classified. This window size was found to be the smallest that enabled the contour boundary to be distinguished from the other image’s artifacts. The output is a single node trained to have an activation of 1.0 for an input window centered in the pixel of a contour boundary, and 0.0 otherwise. The network has a single hidden layer of 30 nodes.
The network was trained using error backpropagation [12, 55] with weight elimination [72] to improve the network’s generalization ability. The training data should be constructed interactively: A proportion of misclassified examples should be added to the training set and used for retraining. The process
376 Giraldi, Rodrigues, Marturelli, and Silva
is initiated from small random selection of contour-boundary and non-contour- boundary examples and should be terminated when a reasonable classification (on a given slice) is achieved.
The MLP classified each pixel independently of the others, and therefore has no notion of a closed contour. Consequently, the contour boundaries it produces are often fragmented and noisy (false negatives and false positives, respectively). Then, with this initial set of points classified as contour boundaries, a deformable model is used to link the boundary segments together, while attempting to ignore
noise.
In [25] the elastic net algorithm is used. This technique is based on the
following equations:
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
||
ut+1 |
|
|
G |
ut |
|
|
2ut |
|
ut |
||||||||
j,l |
|
= |
i=1 |
|
ij |
i,l − |
j,l |
+ |
|
|
j+1,l |
− |
j,l |
+ |
j−1,l |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
utj+,l |
1 |
= K γ utj+,l+1 |
1 − 2utj+,l |
1 + utj+,l−1 |
1 |
|
|
|
|
(7.26) |
|||||||
where utj+,l1 is an interslice smoothing force, K is a simulated annealing term,
α, β, γ are predefined parameters, and Gij is a normalized Gaussian that weights the action of the force that acts over the net point uj,l due to edge point pi,l (l is the slice index).
The deformable model initialization is performed by using a large circle encompassing the lung boundary in each slice. This process can be improved by using the training set.
As an example, let us consider the work [74] in handwritten digit recognition. In this reference, each digit is modeled by a cubic B-spline whose shape is determined by the positions of the control points in the object-based frame. The models have eight control points, except for the one model which has three, and the model for the number seven which has five control points. A model is transformed from the object-based frame to the image-based frame by an affine transformation which allows translation, rotation, dilation, elongation, and shearing. The model initialization is done by determining the corresponding parameters. Next, model deformations will be produced by perturbing the control points away from their initial locations.
There are ten classes of handwritten digits. A feedforward neural network is trained to predict the position of the control points in a normalized 16 × 16 graylevel image. The network uses a standard three-layer architecture. The outputs are the location of the control points in the normalized image. By inverting the


378 |
Giraldi, Rodrigues, Marturelli, and Silva |
in expressions (7.11) and (7.12) have to be properly chosen to guarantee the advance over narrow regions. However, parameters choice remains an open problem in snake models [31]. This problem can be addressed by increasing the grid resolution as it controls the flexibility of T-surfaces. However, this increases the computational cost of the method.
To address the trade-off between model flexibility and the computational cost, in [22, 29] we propose to get a rough approximation of the target surfaces by isosurfaces generation methods. Then T-surfaces model is applied.
The topological capabilities of T-surfaces enable one to efficiently evolve the isosurfaces extracted. Thus, we combine the advantages of a closer initialization, through isosurfaces, and the advantages of using a topologically adaptable deformable model. These are the key ideas of our previous works [22, 29]. We give some details of them.
At first, a local scale property for the targets was supposed: Given an object
O and a point p O , let rp be the radius of a hyperball Bp which contains p and lies entirely inside the object. We assume that rp > 1 for all p O . Hence, the minimum of these radii (rmin) is selected.
Thus, we can use rmin to reduce the resolution of the image without losing the objects of interest. This idea is pictured in Fig. 7.8. In this simple example, we have a threshold which identifies the object (T < 150), and a CF triangulation whose grid resolution is 10 × 10.
Now, we can define a simple function, called an object characteristic function, as follows:
χ ( p) = 1, |
if I ( p) < T, |
(7.27) |
χ ( p) = 0, |
otherwise, |
|
where p is a node of the triangulation (marked grid nodes on Fig. 7.8(a)).
(a) (b)
Figure 7.8: (a) Original image and characteristic function. (b) Boundary approximation.
Improving the Initialization, Convergence, and Memory Utilization |
379 |
We can do a step further, shown in Fig. 7.8( b), where we present a curve which belongs to the transverse triangles. Observe that this curve approximates the boundary we seek. This curve (or surface for 3D) can be obtained by isosurface extraction methods and can be used to efficiently initialize the T-surfaces model, as we already pointed out before.
If we take a grid resolution coarser than rmin, the isosurface method might split the objects. Also, in [22, 29] it is supposed that the object boundaries are closed and connected. These topological restrictions imply that we do not need to search inside a generated connected component.
In [63] we discard the mentioned scale and topological constraints. As a consequence, the target topology may be corrupted. So, a careful approach will be required to deal with topological defects. An important point is the choice of the method to be used for isosurfaces generation. In [22, 63] we consider two kinds of isosurface generation methods: the marching ones and continuation ones.
In marching cubes, each surface-finding phase visits all cells of the volume, normally by varying coordinate values in a triple “for” loop [45]. As each cell that intersects the isosurface is found, the necessary polygon(s) to represent the portion of the isosurface within the cell is generated. There is no attempt to trace the surface into neighboring cells. Space subdivision schemes (such as Octree and k-d-tree) have been used to avoid the computational cost of visiting cells that the surface does not cut [17, 64].
Once the T-surfaces grid is a CF one, the tetra-cubes is especially interesting for this discussion [10]. As in the marching cubes, its search is linear: Each cell of the volume is visited and its simplices (tetrahedrons) are searched to find surfaces patches. Following marching cubes implementations, tetra-cubes uses auxiliary structures based on the fact that the topology of the intersections between a plane and a tetrahedron can be reduced to three basic configurations pictured in Fig. 7.1 (Section 7.2.3).
Unlike tetra-cubes, continuation algorithms attempt to trace the surface into neighboring simplices [1]. Thus, given a transverse simplex, the algorithm searches its neighbors to continue the surface reconstruction. The key idea is to generate the combinatorial manifold (set of transverse simplices) that holds the isosurface.
The following definition will be useful. Let us suppose two simplices σ0, σ1, which have a common face and the vertices v σ0 and v σ1 both opposite
380 |
Giraldi, Rodrigues, Marturelli, and Silva |
the common face. The process of obtaining v from v is called pivoting. Let us present the basic continuation algorithm [1].
PL generation algorithm:
Find a transverse triangle σ0;
= {σ0}; V (σ0) = set of vertices of σ0; while V (σ ) = for some σ
. get σ such that V (σ ) = ;
.get v V (σ );
. |
obtain σ from σ by pivoting v into v |
. |
if σ is not transverse |
. |
then drop v from V (σ ); |
.else
. |
if σ |
|
|
|
|
then |
|
from V (σ |
) |
|
|
|
|
v from V (σ ), v |
|||||
. |
drop |
|
|
|
|||||
. |
else |
|
|
|
|
|
|
|
|
. |
|
= |
+ σ ; |
|
|
|
|||
. |
V (σ |
|
) |
|
set of vertices of σ ; |
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
= |
|
|
|
|
. |
drop v from V (σ ), v |
from V (σ ) |
|||||||
Differently from tetra-cubes, once the generation of a component is started, the algorithm runs until it is completed. However, the algorithm needs a set of seed simplices to be able to generate all the components of an isosurface. This is an important point when comparing continuation and marching methods.
If we do not have guesses about seeds, every simplex should be visited. Thus, the computational complexity of both methods is the same (O (N) where N is the number of simplices).
However, if we know in advance that the target boundary is connected, we do not need to search inside a connected component. Consequently, the computational cost is reduced if continuation methods are applied.
Based on this discussion about marching cubes and PL generation, we can conclude that, if we do not have the topological and scale restrictions given in Section 7.4, tetra-cubes is more appropriate to initialize the T-surfaces. In this case, it is not worthwhile to attempt to reconstruct the surface into neighboring simplices because all simplices should be visited to find surface patches.
However, for the T-surfaces reparameterization (steps (1)–(4) in Section 7.2.3), the situation is different. Now, each connected component is
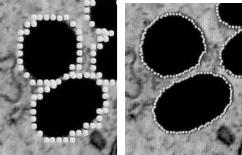
Improving the Initialization, Convergence, and Memory Utilization |
381 |
evolved at a time. Thus a method which generates only the connected component being evolved—that is, the PL generation algorithm—is interesting.
7.5 Reconstruction Method
Following the above discussion, we proposed in [22, 63] a segmentation/surface reconstruction method that is based on the following steps: (1) extract regionbased statistics; (2) coarser image resolution; (3) define the object characteristic function; (4) PL manifold extraction by the tetra-cubes; (5) if needed, increase the resolution, return to step (3); and (6) apply T-surfaces model.
It is important to highlight that T-surfaces model can deal naturally with the self-intersections that may happen during the evolution of the surfaces obtained by step (4). This is an important advantage of T-surfaces.
Among the surfaces extracted in step (4), there may be open surfaces which start and end in the image frontiers and small surfaces corresponding to artifacts or noise in the background. The former is discarded by a simple automatic inspection. To discard the latter, we need a set of predefined features (volume, surface area, etc.) and corresponding lower bounds. For instance, we can set the volume lower bound as 8(r)3, where r is the dimension of the grid cells.
Besides, some polygonal surfaces may contain more than one object of interest (see Fig. 7.9). Now, we can use upper bounds for the features. These upper bounds are application dependent (anatomical elements can be used).
(a) |
(b) |
Figure 7.9: (a) PL manifolds for resolution 3 × 3. ( b) Result with the highest
(image) resolution.
382 |
|
|
|
|
|
|
|
|
|
|
Giraldi, Rodrigues, Marturelli, and Silva |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Figure 7.10: Representation of the multiresolution scheme.
The surfaces whose interior have volumes larger than the upper bound will be processed in a finer resolution. By doing this, we adopted the basic philosophy of some nonparametric multiresolution methods used in image segmentation based on pyramid and quadtree approaches [3, 8, 41]. The basic idea of these approaches is that as the resolution is decreasing, small background artifacts become less significant relative to the object(s) of interest. So, it can be easier to detect the objects in the lowest level and then propagate them back down the structure. In this process, it is possible to delineate the boundaries in a coarser resolution (step (4)) and to re-estimate them after increasing the resolution in step (5).
It is important to stress that the upper bound(s) is not an essential point for the method. Its role is only to avoid expending time computation in regions where the boundaries enclose only one object.
When the grid resolution of T-surfaces is increased, we just reparameterize the model over the finer grid and evolve the corresponding T-surfaces.
For uniform meshes, such as the one in Fig. 7.10, this multiresolution scheme can be implemented through adaptive mesh refinement data structures [5]. In these structures each node in the refinement level l splits into ηn nodes in level l + 1, where η is the refinement factor and n is the space dimension (η = 2 and n = 3 in our case). Such a scheme has also been explored in the context of level sets methods [61].
As an example, let us consider Fig. 7.9. In this image, the outer scale corresponding to the separation between the objects is finer than the object scales. Hence, the coarsest resolution could not separate all the objects. This happens for the bottom-left cells in Fig. 7.9(a). To correct this result, we increase the resolution only inside the extracted region to account for more details (Figure 7.9( b)).
We shall observe that T-surfaces makes use of only the data information along the surface when evolving the model toward the object boundary. Thus, we can
Improving the Initialization, Convergence, and Memory Utilization |
383 |
save memory space by reading to main memory only smaller chunks of the data set, instead of the whole volume, as is usually done by the implementations of deformable surface models. Such point is inside the context of out-of-core methods which are discussed next.
7.6Out-of-Core for Improving Memory Utilization
There are few references of out-of-core approaches for segmentation purposes. The site (graphics.cs.ucdavis.edu/research/Slicer.html) describes a technique based on reordering the data according to a three-dimensional Lebesgue-space- filling-curve scheme to speed up data traversal in disk. The visualization toolkit uses cached, streaming (pulling regions of data in a continual flow through a pipeline) to transparently deal with large data sets [60]. Finally, and more important for our work, out-of-core isosurface extraction techniques have been implemented [16, 64] and can be used for segmentation purposes.
From the viewpoint of out-of-core isosurface generation, we need to efficiently perform the following operations: (a) group spatial data into clusters; ( b) compute and store in disk cluster information ( pointer to the corresponding block recorded in disk, etc.); and (c) optimize swap from disk to main memory. These operations require the utilization of efficient data structures. Experimental tests show that the branch-on-need octree (BONO) [64] and the meta-cell [16] framework provide efficient structures for out-of-core isosurface extraction. Next, we summarize and compare these methods.
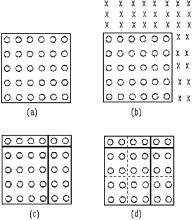
Octrees are hierarchical tree structures of degree 8. If the volume’s resolution is the same power of 2 in each direction; e.g., 2d × 2d × 2d, octrees offer the best ratio of the number of nodes to data points 1/7 [73]. Otherwise, an alternative, to be close to the optimum, is the branch-on-need octree (BONO) strategy [73]. Essentially, the octree is regarded as conceptually full, but the algorithm avoids allocating space for empty subtrees. With each node is associated a conceptual region and an actual region, as illustrated in Fig. 7.11. Besides, at each node the octree contains the maximum and minimum data values found in that node’s subtree.
We shall observe that the same space partition could be obtained if we take the following procedure: Sort all data points by the x-values and partition them
384 |
Giraldi, Rodrigues, Marturelli, and Silva |
Figure 7.11: (a) Data set; ( b) conceptual region; (c) leve 1; and (d) final level.
into H consecutive chunks (H = 3 in Fig. 7.11). Then, for each such chunk, sort its data points by the y-values and partition them into H consecutive chunks. For 3D images we must repeat the procedure for the z-values.
That is precisely the meta-cell partition. Unlike octrees, meta-cell is not a hierarchical structure. The partition is defined through the parameter H. Besides, given a point (q1, q2, q3), inside the domain, the corresponding meta-cell is given by:
mcell = %qi/Ci&, i = 1, 2, 3, |
(7.28) |
where Ci is the number of data points of each chunk of the conceptual region, in the direction i. To each meta-cell is associated a set of meta-intervals (connected components among the intervals of the cells in that meta-cell). These metaintervals are used to construct an interval tree, which will be used to optimize I/O operations. Given a set of N meta-intervals, let e1, e2, . . . , e2n be the sorted list of left and right endpoints of these intervals. Then, the interval tree is recursively defined as follows:
Interval tree construction: (i) If there is only one interval, then the current node r is a leaf containing that interval; (ii) else, the value m = (en + en+1)/2 is stored in r as a key; the intervals that contain m are assigned to r as well as pointers to the subtrees left(r) and right(r). Go to step (i).
Now, let us take an overview of out-of-core isosurface extraction methods based on the above structures. The methodology presented in [64] extends the BONO for time-varying isosurface extraction. The proposed structure (temporal
