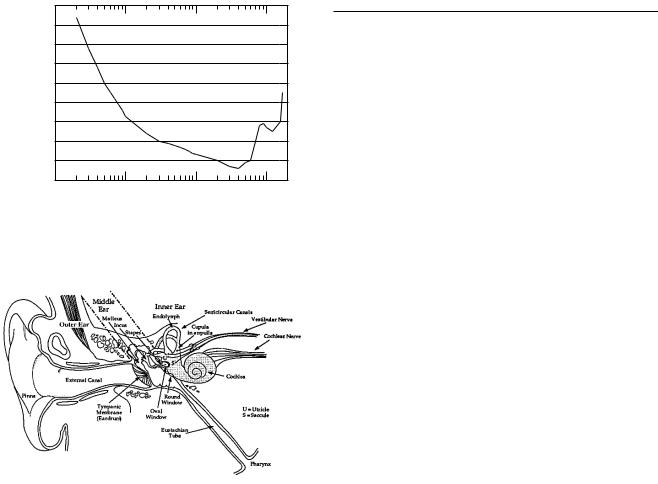
Intermediate Physics for Medicine and Biology - Russell K. Hobbie & Bradley J. Roth
.pdf


|
References |
341 |
Barrett, H. H., and K. J. Myers (2004). Foundations of |
Ramachandran, G. N., and A. V. Lakshminarayanan |
|
Image Science. New York, Wiley-Interscience. |
(1971). Three-dimensional reconstruction from radi- |
|
Cho, Z.-h., J. P. Jones, and M. Singh (1993). Founda- |
ographs and electron micrographs: Application of con- |
|
tions of Medical Imaging. New York, Wiley. |
volutions instead of Fourier transforms. Proc. Nat. Acad. |
|
Delaney, C., and J. Rodriguez (2002). A simple medical |
Sci. U.S. 68: 2236–2240. |
|
physics experiment based on a laser pointer. Amer. J. |
Shaw, R. (1979). Photographic detectors. Ch. 5 of Ap- |
|
Phys. 70(10): 1068–1070. |
plied Optics and Optical Engineering, New York, Acad- |
|
Gaskill, J. D. (1972). Linear Systems, Fourier Trans- |
emic, Vol. 7, pp. 121–154. |
|
forms, and Optics. 3rd. ed. New York, Wiley. |
Williams, C. S., and O. A. Becklund (1972). Optics: |
|
Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. |
A Short Course for Engineers and Scientists. New York, |
|
P. Flannery (1992). Numerical Recipes in C: The Art of |
Wiley. |
|
Scientific Computing, 2nd ed., reprinted with corrections, |
|
|
1995. New York, Cambridge University Press. |
|
|
Sound (or acoustics) plays two important roles in our |
x |
x + dx |
|
study of physics in medicine and biology. First, ani- |
|
|
|
mals hear sound and thereby sense what is happening in |
|
|
|
their environment. Second, physicians use high-frequency |
|
|
|
sound waves (ultrasound ) to image structures inside the |
|
(a) |
|
body. This chapter provides a brief introduction to the |
|
|
|
physics of sound and the medical uses of ultrasonic imag- |
ξ(x,t) |
ξ (x + dx,t) |
|
ing. A classic textbook by Morse and Ingard (1968) pro- |
|
|
|
vides a more thorough coverage of theoretical acoustics, |
|
|
|
and books such as Hendee and Ritenour (2002) describe |
sn(x,t) |
sn(x + dx,t) |
|
the medical uses of ultrasound in more detail. |
|
(b) |
|
In Sec. 13.1 we derive the fundamental equation gov- |
|
||
|
|
||
erning the propagation of sound: the wave equation. Sec- |
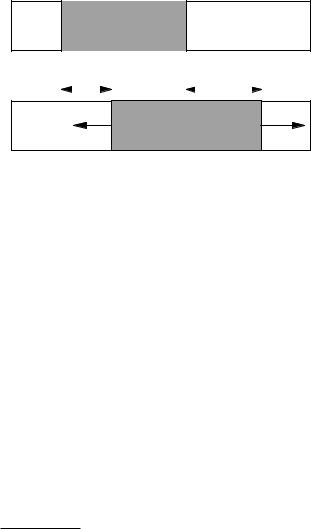
FIGURE 13.1. An elastic rod. (a) The rod in its equilibrium |
||
tion 13.2 discusses some properties of the wave equation, |
position. (b) Each point on the rod has been displaced from its |
||
including the relationship between frequency, wavelength, |
equilibrium position by an amount ξ which depends on x and |
||
and the speed of sound. The acoustic impedance and |
t. As a result there is a normal stress sn which also depends |
||
its relevance to the reflection of sound waves are intro- |
on x and t. |
|
|
|
|
||
duced in Sec. 13.3. Section 13.4 describes the intensity |
|
|
|
of a sound wave and develops the decibel intensity scale. |
rium position. In this section we consider sound waves |
||
The ear and hearing are described in Sec. 13.5. Section |
propagating along the x axis. The results can be general- |
||
13.6 discusses attenuation of sound waves. Physicians use |
ized to three dimensions [See Morse and Ingard (1968)]. |
||
ultrasound imaging for medical diagnosis, as described in |
We first consider an elastic rod, and then a fluid in which |
||
Section 13.7. Ultrasonic imaging can provide information |
viscous e ects are not important. |
||
about the flow of blood in the body by using the Doppler |
|
|
|
e ect, as shown in Sec. 13.8. |
13.1.1 Plane Waves in an Elastic Rod |
||
|
|
||
13.1 |
The Wave Equation |
The simplest case to consider is an elastic rod which is |
|
forced to move longitudinally at one end. This results in |
|||
In Chapter 1, we assumed that solids and liquids are in- |
the propagation of a sound wave along the rod.1 We set up |
||
a coordinate system where x measures distance along the |
|||
compressible. If a long rod were truly incompressible, a |
rod from a fixed origin when no sound wave is traveling |
||
displacement of one end would instantly result in an iden- |
along the rod. We also assume that the disturbance of |
||
tical displacement of the other end. In fact, the displace- |
the rod depends only on the position along the rod, x, |
||
ment does not propagate instantaneously. It travels at the |
|
|
|
speed of sound in the rod. |
1This simple geometry assures that all motion is parallel to the x |
||
The propagation of sound involves small displacements |
axis. In general, motion in an elastic solid involves both longitudinal |
||
of each volume element of the medium from its equilib- |
waves and transverse waves. |
|
|