5.4.2 Абсолютно неупругий удар

Пусть абсолютно не упруго сталкиваются два тела с массами т₁и т₂, движущихся со скоростямии. Считаем, что тела образуют замкнутую систему. По закону сохранения импульса

.

Отсюда скорость после столкновения равна

.

Из этой формулы видно, что после столкновения тела двигаются вдоль диагонали параллелограмма, построенного на векторах и.

Закон сохранения суммарной энергии в случае абсолютно неупругого удара запишется в виде

+ А_деформ.

5.5. Задание для самоконтроля знаний

_{1. Определить скорость вагонов одинаковой массы после неупругого столкновения, если они двигались навстречу со скоростями и} .

2. На сколько изменится угловая скорость фигуриста при его вращении, если он изменит свой момент инерции в 2 раза.

_{3. Определить потенциальную, кинетическую и полную энергию тела массой 1кг падающего с высоты 2м на середине пути и в точке удара о Землю.}

_{4. Определить скорость второго шара u2 после упругого столкновения его с первым шаром, движущимся со скоростью υ1 = 10 м/с, если их массы равны, а до столкновения скорость второго шара υ2 = 0 м/с.}

_{5. Определить скорость двух вагонов массой 10т, движущихся вместе после их не упругого столкновения, когда один стоял, а другой двигался со скоростью 20 км/час.}

Лекция 7

Глава 6. Механические волны

6.1 Продольные и поперечные волны

Е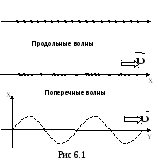сли какую-либо частицу или совокупность частиц упругой среды привести в колебательное движение, то колебания не останутся локализованными в том месте, где они возникли, а благодаря взаимодействию между частицами будут распространяться с некоторой скоростью по всем направлениям.Процесс распространения механических колебаний в упругой среде называется механической волной.

В волне частицы среды лишь совершают колебания около положений равновесия, причем соседние частицы, даже самые ближайшие, колеблются с некоторым сдвигом по фазе. Наличие сдвига фаз объясняется упругим взаимодействием между частицами которое распространяется в среде с конечной скоростью.

Различают поперечные и продольные волны. Волна называется поперечной, если колебания частиц среды происходят вдоль направлений, перпендикулярных к направлению распространения волны (например, колебания струны). Поперечные волны могут распространяться в тех средах, в которых возникают упругие силы при деформации сдвига.

Волна называется продольной, если колебания частиц среды происходят вдоль направлений, параллельных направлению распространения волны (например, звуковые волны). Продольные волны распространяются в упругих средах при их сжатии или растяжении

Расположение частиц в упругой среде в момент возникновения продольной или поперечной волны приведены на рис. 6.1. До появления волны частицы среды вдоль направления хнаходились на одинаковых расстояниях.

Распространение волны в упругой среде происходит с фазовой скоростью , частотой колебаний, периодом колебаний Т, циклической частотойи длиной.

Фазовая скорость, или скорость распространения волны , - это скорость с которой перемещается в пространстве фаза колебания. Фазовая скорость зависит от плотности среды и ее упругих свойств.

Частота колебаний - число полных колебаний частиц среды за единицу времени.

Период колебаний Т – промежуток времени, в течение которого частицы совершает одно полное колебание.

Циклическая частота - число полных колебаний, совершаемых за 2секунд.

Длина волны– расстояние между ближайшими частицами, с одинаковой фазой или сдвигом фаз равным 2.

Волновая поверхность – это геометрическое место точек, колеблющихся в одинаковой фазе. Волновые поверхности проводятся через равновесные положения частиц, колеблющихся в одинаковых фазах и поэтому они неподвижны. В зависимости от формы волновой поверхности различают плоские, сферические, цилиндрические, эллиптические волны и др.

Поверхность, отделяющая колеблющиеся частицы от частиц, находящихся в покое называется фронтом волны. Фронт волны в отличие от волновых поверхностей перемещается со скоростью, равной скорости распространения волны.

Нормаль восстановленная в точке фронта волны определят направление распространения волны.

Параметры волны связаны между собой соотношениями

(6.1)

Отношение называется волновым числом.

2. Уравнение плоской гармонической волны. Волновое уравнение.

Уравнение волны позволяет найти смещение sлюбой частицы среды от ее положения равновесия. Смещение зависит от координат частицы и времениs(x,y,z,t) и является периодической функцией.

Будем считать, что частицы среды совершают гармонические колебания и образуют плоскую волну движущихся в направлении осих.

Выделим в среде две волновые поверхности так, чтобы одна проходила через начало координат (поверхность О), другая – через произвольную точку с координатойх(поверхность Х) (рис. 6.2). Пусть смещение частиц принадлежащих волновой поверхностиО, изменяется какКолебания частиц, принадлежащих поверхностиХ, начнутся позже, так как требуется время за которое волна проходит расстояниех, отделяющее поверхностиОиХ.

Смещения частиц поверхности Хбудут отставать по времени от аналогичных смещений частиц поверхностиОнаи для них

(6.2)

Уравнение (6.2) – есть уравнение плоской гармонической волны, распространяющейся в направлении оси х.sопределяет смещение от положения равновесия любой из частиц с координатойхв момент времениt, А – максимальное смещение.

Запишем уравнение волны

(6.3)

где волновое плечо.

Уравнение волны, распространяющейся в направлении, противоположном оси, имеет вид

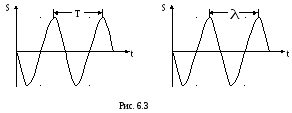
График и функции s(t) иs(x) при некотором фиксированном значениих иtприведены на рис. 6.3.

Уравнение плоской волны получается в результате решения волнового дифференциального уравнения в котором вторые частные производные от смешения по координатам связаны со вторыми производными от смещения по времени.

продифференцируем уравнение волны (6.3) дважды по времениt и координатой хи полученные равенства поделим

Так как то, и волновое уравнение плоской гармонической волны запишется в виде

_(6.4)

Для волны распространяющейся в произвольном направлении, в левой части волнового уравнения появляются вторые частные производные по yиz

_(6.5)

Приведем формулы для расчета скорости распространения волны в разных средах, которые могут быть полезны при решении инженерных задач.

1. В растянутой струне скорость распространения поперечной волнызависит от силы натяжения струныи от ее массы, приходящейся на единицу длины, (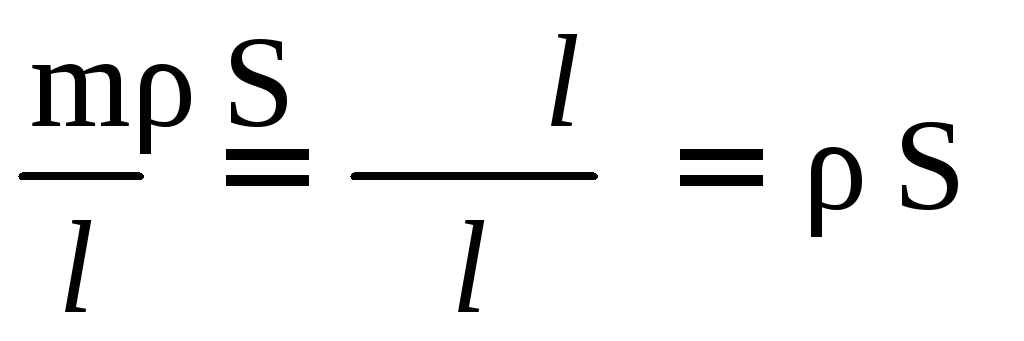, где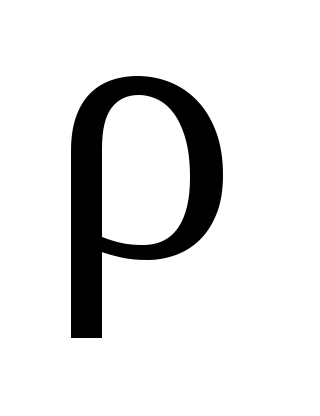– плотность материала,S– площадь поперечного сечения,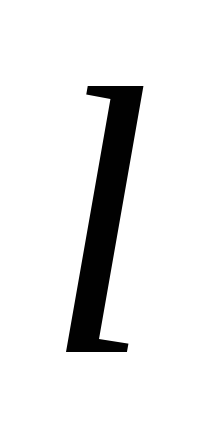- длина струны)

.

2. Скорость распространения колебаний в твердом тонком стержне для продольной волны

,

и поперечной волны ,

где Е – модуль Юнга, G– модуль сдвига,- плотность материала стержня.

3. Скорость распространения звуковой волны в идеальном газе

,

где – показатель адиабаты, Т – температура,R– универсальная газовая постоянная,– молярная масса газа.