
- •Механика
- •Оглавление
- •Глава 1. Кинематика материальной точки
- •Глава 2. Динамика
- •Глава 3. Работа и энергия
- •Глава 4. Законы сохранения в механике
- •Глава 5. Механические волны
- •Глава 6. Молекулярное движение
- •Глава 7. Основы термодинамики
- •Глава 1. Кинематика материальной точки
- •Кинематика поступательного движения
- •Понятия и определения
- •Модуль вектора ускорения
- •1.2. Уравнения движения
- •1.2.1 Равномерно, прямолинейно движение.
- •1.2.2 Ускоренное, прямолинейное движение
- •1.2.3 Кинематика вращательного и колебательного движения Вращательное движение
- •При постоянной угловой скорости , угловой путь и угол поворота определяется из равенств:
- •Колебательное движение
- •Для самостоятельного изучения
- •1.3.1 Модуль касательного и нормального ускорения.
- •1.3.2 Равномерное криволинейное движение.
- •Сложение гармонических колебаний
- •1.4 Задания для самоконтроля знаний.
- •Глава 2. Динамика
- •2.1 Законы Ньютона.
- •2.2. Динамика поступательного движения тела
- •2.3. Динамика вращательного движения
- •2.4. Динамика колебательного движения
- •2.5. Принцип относительности Галилея. Неинерциальные системы отсчета
- •2.6 Для самостоятельного изучения
- •2.6.1. Понятие силы. Равнодействующая сила
- •2.6.2. Силы гравитационного взаимодействия
- •2.6.3.Силы трения
- •2.6.4.Сила вязкого трения и сопротивления среды.
- •2.6.5.Сила упругости. Закон Гука.
- •6. Колебания математического и физического маятников
- •2.7. Задания для самоконтроля знаний
- •Глава 3. Работа и энергия
- •3.1. Работа. Мощность
- •3.2. Энергия поступательного движения (кинетическая энергия)
- •И всегда положительна в любой системе отсчета.
- •3 Dr.3. Энергия взаимодействия (потенциальная энергия)
- •3.4. Работа и энергия вращательного движения
- •3.5. Энергия колебательного движения
- •3.6. Для самостоятельного изучения
- •3.6.1. Потенциальная энергия тела относительно поверхности Земли
- •3.6.2. Работа силы тяжести
- •3.6.3. Потенциальная энергия пружины
- •3.6.4. Потенциальный барьер и яма
- •3.7. Задание для самоконтроля знаний.
- •Лекция 6
- •Глава 5. Законы сохранения в механике
- •5.1 Закон сохранения импульса
- •5.2 Закон сохранения момента импульса
- •При составлении равенства (5.5) учтено, что и.
- •5.3 Закон сохранения энергии
- •5.4 Для самостоятельного изучения
- •5.4.2 Абсолютно неупругий удар
- •5.5. Задание для самоконтроля знаний
- •Глава 6. Механические волны
- •6.1 Продольные и поперечные волны
- •6.3.Задания для самоконтроля знаний.
- •Глава 7.Молекулярное движение
- •7.1 Размеры и масса молекул
- •7.2. Движение и столкновение молекул газа
- •7.3 Давление и температура.
- •7.4 Скорость и энергия молекул [распределение Максвелла]
- •7.5 Диффузия, внутреннее трение, теплопроводность.
- •7.6 Давление идеального газа на стенку
- •7.7 Уравнение состояния идеального газа
- •Глава 8. Основы термодинамики
- •8.1. Термодинамическая система. Внутренняя энергия идеального газа
- •8.2. Работа и теплопередача
- •8.3. Первое начало термодинамики, термодинамические изопроцессы.
- •8.4 Теплоемкость
- •8.5 Обратимые и необратимые процессы. Термодинамическая вероятность. Энтропия.
- •8.6 Изменение энтропии в изопроцессах
- •8.7 Тепловая машина. Цикл Карно.
- •8.8. Для самостоятельного изучения
- •1. Второе начало термодинамики
- •Вес тела – сила, приложенная к опоре или подвесу, которые удерживают тело от свободного падения. При неподвижной опоре (подвесе) или при их равномерном движении вес тела равен силе тяжести.
- •Второй закон Ньютона - ускорение , материальной точкой в инерциальной системе отсчета прямопропорционально действующей силе, обратно пропорционально массе и совпадает по направлению с силой.
- •Вес тела – сила, приложенная к опоре или подвесу, которые удерживают тело от свободного падения. При неподвижной опоре (подвесе) или при их равномерном движении вес тела равен силе тяжести.
Для самостоятельного изучения
1.3.1 Модуль касательного и нормального ускорения.
Модули касательного и нормального ускорения находятся из соотношения
, (1.38)
где
![]() единичный
вектор, направленный по касательной к
точке траектории в сторону движения
м.т. (рис 1.11), а
единичный
вектор, направленный по касательной к
точке траектории в сторону движения
м.т. (рис 1.11), а![]() -
вектор мгновенной скорости
-
вектор мгновенной скорости![]() .
.
Первое слагаемое в (1.11) равно касательному ускорению,
![]() ,
,
![]()
![]()
 ,
,![]()
второе - нормальному
![]()
![]() (1.39)
(1.39)
Вектор касательного ускорения может
совпадать с вектором мгновенной скорости
![]() и может быть ему антипараллелен
и может быть ему антипараллелен![]() .
В первом случае движение будет ускоренным,
а во втором – замедленным.
.
В первом случае движение будет ускоренным,
а во втором – замедленным.
Рассмотрим перемещение материальной
точки по траектории из точки
![]() в точку
в точку![]() .
(рис 1.7) За малый интервал времени
.
(рис 1.7) За малый интервал времени![]() единичный вектор в точке А2 равен
сумме
единичный вектор в точке А2 равен
сумме
![]() ,
,
где
![]() – единичный вектор, определяющий
направление движения в точке А1,
– единичный вектор, определяющий
направление движения в точке А1,![]() – вектор изменения направления движения.
Треугольник
– вектор изменения направления движения.
Треугольник![]() ,
образованный векторами
,
образованный векторами![]() и
и![]() ,
равнобедренный, т.к.
,
равнобедренный, т.к.![]() =1.
При
=1.
При![]() ,
угол
,
угол![]() между векторами
между векторами![]() и
и![]() уменьшается
и стремится к нулю, а угол
уменьшается
и стремится к нулю, а угол![]() между векторами
между векторами![]() и
и![]() увеличится до
увеличится до![]() .
Следовательно, вектора
.
Следовательно, вектора![]() и
и![]() направлены к центру кривизны траектории
и совпадает с вектором нормали к
скорости
направлены к центру кривизны траектории
и совпадает с вектором нормали к
скорости![]() (
(![]() ).
).
Модуль вектора нормального ускорения
определяется из треугольников
![]()
![]() и
и![]() DC.
Эти треугольники равнобедренные и
подобные, т.к. при
DC.
Эти треугольники равнобедренные и
подобные, т.к. при![]()
![]() где
где![]() –
радиус кривизны траектории. Из соотношения
сторон треугольников
–
радиус кривизны траектории. Из соотношения
сторон треугольников
. (1.40)
Для бесконечного малого интервала
времени![]() ,
,
![]()
Вектор
![]() можно представить в виде
можно представить в виде
![]() .
Тогда вектор нормального ускорения
.
Тогда вектор нормального ускорения
![]() ,
,
![]() (1.41)
(1.41)
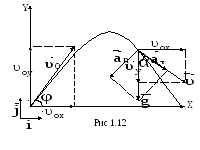
1.3.2 Равномерное криволинейное движение.
Частным случаем ускоренного движения
является движение тела брошенного со
скоростью
![]() под
углом
под
углом![]() к горизонту и падающего с постоянным
ускорением свободного падения
к горизонту и падающего с постоянным
ускорением свободного падения![]() (рис
1.12). Положение тела в пространстве
определяется путем разложения его
движения на равномерное прямолинейное
по оси OX со скоростью
(рис
1.12). Положение тела в пространстве
определяется путем разложения его
движения на равномерное прямолинейное
по оси OX со скоростью![]() и равнопеременное по оси OY с ускорением
свободного падения g и начальной
скоростью
и равнопеременное по оси OY с ускорением
свободного падения g и начальной
скоростью![]() .
.
В момент времени t координаты тела
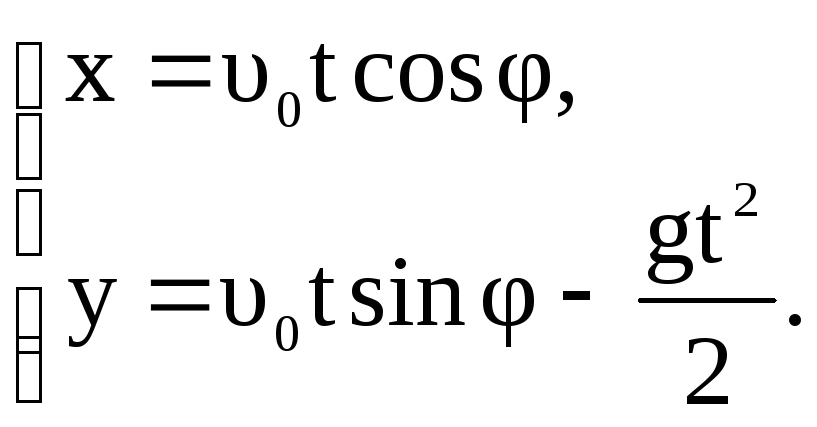 (1.42)
(1.42)
вектор скорости
![]() .
(1.43)
.
(1.43)
Модуль вектора скорости
![]() (1.44)
(1.44)
где
![]() .
.
Уравнение траектории найдём путем исключения параметра tиз равенств (1.44)
![]() .
(1.45)
.
(1.45)
Ускорение свободного падения в любой точке траектории можно разложить на его касательную и нормальную составляющие, где модуль касательного ускорения
![]()
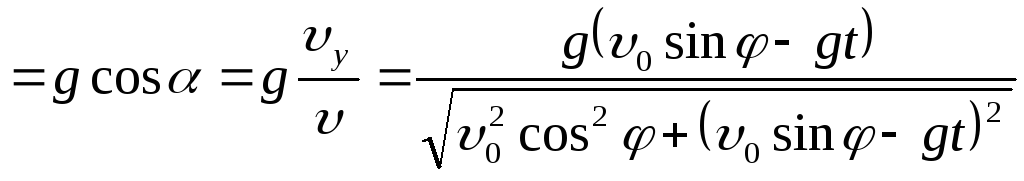 ,
(1.46)
,
(1.46)
где α-угол между векторами скорости
![]() и ускоренияgв заданной
точке траектории
и ускоренияgв заданной
точке траектории
Модуль нормального ускорения
![]() . (1.47)
. (1.47)
Из сравнения уравнения параболы
![]() и равенства (1.22) следует, что тело,
брошенное под углом к горизонту, движется
по параболе.
и равенства (1.22) следует, что тело,
брошенное под углом к горизонту, движется
по параболе.
