2.1.6 Розкладання сум квадратів

Відповідно до основної ідеї дисперсійного аналізу розкладемо суму квадратів відхилень спостережень від загального середнього на дві скла-дові суми, одна з яких буде характеризувати вплив фактора випадковості, а друга - фактора мінливості х.

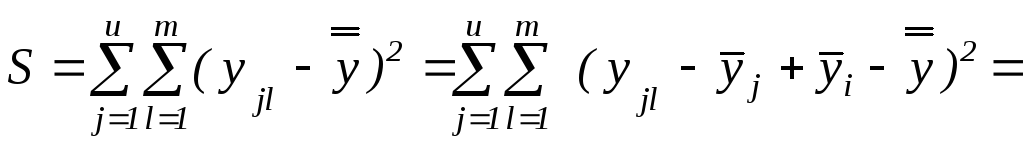
(2.7)

,

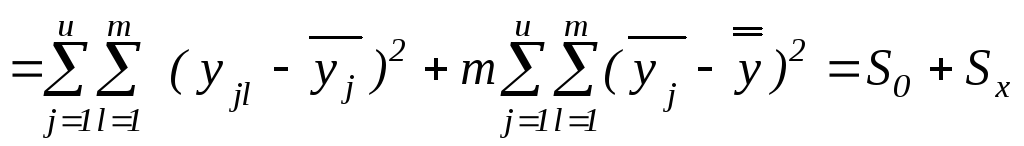оскільки

, (2.8)

а

,

як сума відхилень спостережень j-ї серії від середнього тієї самої серії, де

(2.9)

- “загальна” сума квадратів відхилень окремих спостережень від загального середнього . Ця сума характеризує розсіювання спостережень в результаті дії обох факторів як випадковості (з дисперсією ²), так і досліджуваного x (з дисперсією ²).

(2.10)

- сума квадратів відхилень "в середині серій", тобто сума квадратів роз-ходжень між окремими спостереженнями і середнімвідповідної се-рії. Ця сума характеризує залишкове розсіювання випадкових похибок дос-віду, тобто їхнє відтворення (з дисперсією²).

(2.11)

- сума квадратів відхилень "між серіями" або розсіювання за рівнями, тобто зважена (з урахуванням кількості спостережень в кожній серії) сума квадратів різниць між середнім окремих серій і загальним середнімвсієї сукупності спостережень. Сумахарактеризує розсіювання серед-ніхсерій за рахунок випадкових причин (з дисперсією для середніх серій) і досліджуваного фактора (з дисперсією).

2.1.7 Оцінка дисперсій

Припустимо, що вплив фактора x на вихідний параметр буде відсут-ній, тобто нуль-гіпотеза про однорідність вірна. Тоді всі серії паралельних спостережень можна розглядати як випадкові вибірки з однієї і тієї самої нормальної сукупності і, отже:

1) не зміщена загальна оцінка дисперсій відновлення ² за всіма u·m спостереженнями визначається з виразу

(2.12)

з кількістю ступенів свободи

2) вибіркова дисперсія розсіювання "в середині серій" або залиш-кова оцінка дисперсії відновлення ² знаходиться як середнє з вибіркових дисперсій за кожною серією окремо

(2.13)

з кількістю ступенів свободи

3) вибіркова дисперсія розсіювання між середніми серій є незміщеною оцінкою дисперсії , а нормально розподілені (незалежні одна від іншої) середні серій:

(2.14)

з кількістю ступенів свободи

Звідси легко отримуємо третю оцінку дисперсії відновлення, вибіркову дисперсію розсіювання "між серіями":

(2.15)

з кількістю ступенів свободи

Кількість ступенів свободи перевіряється зі співвідношення

4) В результаті більш глибокого аналізу можна довести, що S₀ і S_x незалежні один від одного. Зі сказаного видно, що через відсутність впливу фактора x вибіркові оцінки s², і s_x однорідні, оскільки є оцінками однієї і тієї самої генеральної дисперсії ².

Припустимо тепер, що вплив фактора x на вихідний параметр істотний, тобто нуль-гіпотеза про однорідність вірна. Тоді серії паралельних спостережень можна розглядати як випадкові вибіркиu незалежних нормально розподілених випадкових величин з однією і тією ж дисперсією ² та різними центрами розподілу . Отже:

1) вибіркова дисперсія s² характеризує вплив як фактора випадковості, так і фактора x, тобто

; (2.16)

2) оскільки сума S₀ не змінюється при заміні нато вибіркова дисперсія також не змінюється і так само є не зміщеною оцінкою для ², тобто

; (2.17)

3) оскільки сума S_x враховує не тільки випадкові, але й систематичні розходження між середніми серій і збільшується за рахунок впливу фактора x, то дисперсія при цьому також збільшується і перестає бути оцінкою тільки для , тобто

Тому легко отримуємо

(2.18)

4) незалежність S₀ і S_x один від іншого зберігається.

Таким чином, для дисперсії фактора x тепер можна дати дві наближені оцінки

(2.19)

(2.20)

Перша оцінка менш точна через похибки величин s² і . Точність другої вище, оскільки дисперсії, які входять в неї, поділені на m.

Виходячи з другого припущення зрозуміло, що за умови впливу фактора x вибіркові оцінки s², , s_x неоднорідні. Отже, зіставляючи ці вибіркові дисперсії, можна прийняти рішення про справедливість першого або другого припущення щодо значимості впливу фактора x (з дисперсією ) на вихідний параметр. З огляду на точність виразів (2.19), (2.20), для оцінки будемо порівнювати дисперсіїі.