- •Федеральное агентство морского и речного транспорта
- •Предисловие
- •Лекция 1. Предмет физики.
- •1. Кинематика. Движение тел.
- •2. Движение материальной точки.
- •3. Скорость.
- •4. Ускорение.
- •5. Вращательное движение. Угловая скорость и угловое ускорение.
- •6. Качение тела.
- •Лекция 2. Динамика материальной точки.
- •1. Первый закон Ньютона.
- •2. Второй закон Ньютона.
- •3. Третий закон Ньютона.
- •4. Закон всемирного тяготения. Сила тяжести. Вес.
- •Силы упругости.
- •Силы трения.
- •Лекция 3. Закон сохранения импульса.
- •Введение.
- •Закон сохранения импульса.
- •Закон движения центра масс.
- •Движение тел с переменной массой. Реактивное движение.
- •Лекция 4. Закон сохранения энергии в механике.
- •Энергия, работа, мощность.
- •Потенциальная энергия.
- •Кинетическая энергия
- •Закон сохранения энергии.
- •Удар абсолютно упругих и абсолютно неупругих тел.
- •Лекция 5. Динамика вращательного движения твердого тела.
- •Вращение твердого тела вокруг неподвижной оси. Кинетическая энергия.
- •2. Момент инерции твердого тела.
- •3. Моменты инерции тел различной формы.
- •4. Момент силы относительно неподвижной точки.
- •5. Момент силы относительно неподвижной оси.
- •6. Момент импульса относительно неподвижной точки.
- •7. Момент импульса относительно неподвижной осиz.
- •Лекция 6. Уравнения динамики вращательного движения.
- •1. Закон сохранения момента импульса.
- •2. Гироскоп.
- •Лекция 7 Колебания и волны.
- •Свободные гармонические колебания. Гармонический осциллятор.
- •Задача о колебании груза на пружине.
- •Задача о физическом маятнике.
- •Задача о математическом маятнике.
- •Скорость и ускорение при гармоническом колебании.
- •Энергия гармонического осциллятора.
- •Лекция 8. Сложение колебаний.
- •Сложение гармонических колебаний одного направления и одной частоты.
- •Биения.
- •Формула для сложения колебаний в общем случае для плоских волн.
- •Вынужденные колебания.
- •Затухающие колебания.
- •Механические волны (упругие волны)
- •Лекция 9 Уравнение плоской гармонической волны.
- •Фронт волны
- •Фазовая скорость.
- •Волновое уравнение.
- •Стоячие волны.
- •Звуковые волны.
- •Лекция 10 Механика жидкости
- •Линии и трубки тока. Неразрывность струи.
- •Уравнение Бернулли.
- •Ламинарное и турбулентное течение.
- •Силы сопротивления при движении тел в жидкостях. Закон Стокса. Число Рейнольдса.
- •Лекция 11 Физические основы молекулярно-кинетической теории газов.
- •1. История.
- •2. Идеальный газ. Параметры состояния газа. Уравнение состояния идеального газа.
- •3. Атомная единица массы (а.Е.М.).
- •4. Свойства идеального газа.
- •5. Уравнение Менделеева-Клапейрона.
- •6. Основное уравнение кинетической теории газов (уравнение Клаузиуса).
- •Лекция 12 Первый закон термодинамики.
- •1. Термодинамические системы (тдс).
- •2. Внутренняя энергия систем.
- •3. Первый закон термодинамики. Термодинамические процессы.
- •4. Работа газа при изменении его объема.
- •5. Теплоемкость.
- •Лекция 13 Термодинамические процессы.
- •1. Изохорный процесс
- •2. Изобарный процесс.
- •3. Изотермический процесс.
- •Лекция 14
- •4. Адиабатический процесс.
- •5. Политропический процесс.
- •Лекция 15 Второе начало термодинамики. Сущность второго начала термодинамики.
- •1. Введение
- •2. Обратимые и необратимые процессы.
- •3. Круговые процессы (циклы).
- •4. Прямой цикл (тепловая машина).
- •5. Обратный цикл (холодильник).
- •6. Цикл Карно. Произвольный обратимый цикл.
- •Лекция 16 Энтропия.
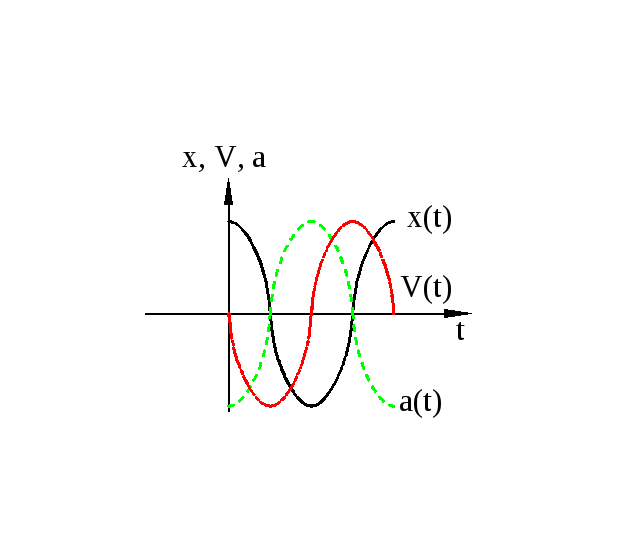
Скорость и ускорение при гармоническом колебании.
![]()
![]() =
=![]()
![]() - амплитудное значение скорости
- амплитудное значение скорости
![]()
Скорость опережает смещение по фазе на
![]() .
.
![]() =
=![]()
![]()
![]()
Сдвиг фаз между
![]() и
и![]() равен
равен![]() ,
они колеблются в противофазах.
,
они колеблются в противофазах.
Сила.
![]()
Силы, которые подчиняются закону упругой силы, но по природе своей не являются упругими называются квазиупругими.
Гармонические колебания – это колебания, которые происходят под действием квазиупругой силы, то есть силы, пропорциональной смещению.
Энергия гармонического осциллятора.
![]()
(кинетическая Энергия, Т + потенциальная энергия, П = полной энергии, Е).
Пусть
![]()
![]() .
.
Тогда
![]() =
=![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]() =
=![]() +
+![]() =
=![]() .
.
![]()
- полная энергия механического осциллятора
не зависит от
![]() и пропорциональна
и пропорциональна![]() .
Механический осциллятор есть консервативная
система, так как
.
Механический осциллятор есть консервативная
система, так как![]() .
.
Выводы:
Кинетическая и потенциальная энергии по отдельности зависят от времени.
Максимальная кинетическая энергия равна максимальной потенциальной энергии и равна полной энергии.
Средняя кинетическая энергия равна средней потенциальной энергии и равна половине полной энергии.
Полная энергия не зависит от времени и пропорциональна квадрату амплитуды.
Лекция 8. Сложение колебаний.
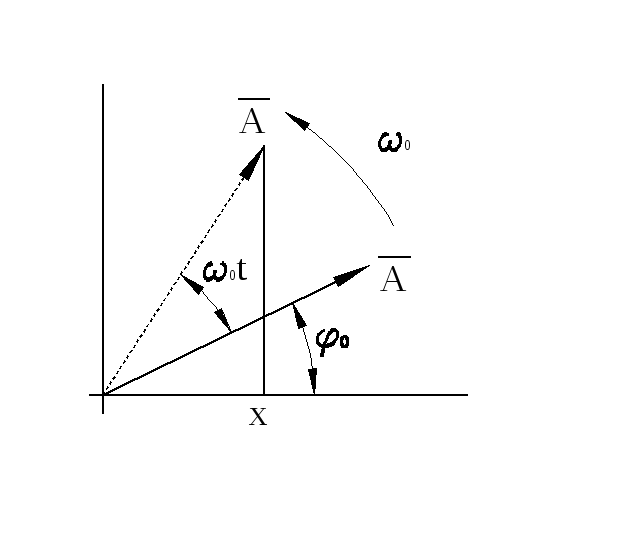
Сложение колебаний – задача сложная и часто пользуются искусственными приемами для ее решения. Представим гармоническое колебание в виде вектора амплитуды.
|
|
Модуль
вектора
|
В момент
![]() проекция на ось
проекция на ось![]() вектора
вектора![]() равна
равна![]() .
Получили уравнение гармонических
колебаний. Итак, всякому гармоническому
колебанию можно сопоставить вектор
амплитуды, вращающийся с угловой
скоростью
.
Получили уравнение гармонических
колебаний. Итак, всякому гармоническому
колебанию можно сопоставить вектор
амплитуды, вращающийся с угловой
скоростью![]() ,
равной круговой частоте колебания.
Тогда проекция этого вектора на ось
,
равной круговой частоте колебания.
Тогда проекция этого вектора на ось![]() совершает гармонические колебания.
Физического смысла здесь нет, но решение
задачи облегчается.
совершает гармонические колебания.
Физического смысла здесь нет, но решение
задачи облегчается.
Сложение гармонических колебаний одного направления и одной частоты.
![]()
![]() .
.
Изобразим их графически:
|
|
|
Векторы
![]() и
и![]() вращаем с
вращаем с![]() .
Поскольку частоты равны, то параллелограмм,
не деформируясь, вращается с той же
частотой. Длина
.
Поскольку частоты равны, то параллелограмм,
не деформируясь, вращается с той же
частотой. Длина![]() не
меняется. Его проекция совершает
гармонические колебания.
не
меняется. Его проекция совершает
гармонические колебания.
![]() ,
но
,
но![]() .
.
То есть результирующее колебание гармоническое, имеет ту же частоту, что и слагаемые колебания. Амплитуду находим из начальных условий по формуле
![]()
![]() ,
,
![]()
Биения.
Рассмотрим сложение колебаний одинаковой
амплитуды и близких частот
![]() ,
,![]() ,
,![]() .
Решение задачи усложняется.
.
Решение задачи усложняется.
![]()
![]() .
.
Если изобразить эти колебания с помощью
вектора амплитуды, то они вращаются с
разными угловыми скоростями, и всегда
будет момент, когда
![]() .
Фазы в этот момент принимают за нуль.
Тогда
.
Фазы в этот момент принимают за нуль.
Тогда
![]()
![]() .
.
![]() =
=![]()
![]() =
=
=
![]() .
.
![]() =
=![]()
- уравнение биений. Первый множитель медленно меняется, второй – быстро. Уравнение можно представить в виде
![]()
Сравним с уравнением гармонических колебаний
![]() .
.
Уравнение биений – негармоническое,
но
![]() меняется медленно, так как
меняется медленно, так как![]() мало.
мало.
![]() .
.
Поэтому биения – приблизительно
гармонические колебания с медленно
меняющейся амплитудой,
![]() может быть больше и меньше нуля.
может быть больше и меньше нуля.
![]() - амплитуда. Для гармонических колебаний
- амплитуда. Для гармонических колебаний
|
|
|
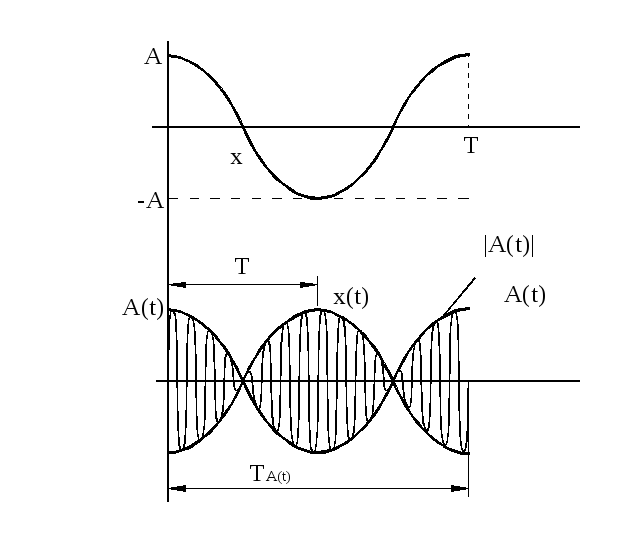
Амплитуда ограничивает
![]() .
(Проводим штрихами симметричную кривую
внизу).Частота
.
(Проводим штрихами симметричную кривую
внизу).Частота![]() .
.![]() .
Получили биения – усиление и ослабление
колебаний.
.
Получили биения – усиление и ослабление
колебаний.
Метод биений широко применяется на практике. Основан на сравнении искомой частоты с частотой эталона. Метод биений – это один из наиболее точных методов измерения частот, емкостей, индуктивностей. Применяют для настройки музыкальных инструментов.