Система разностных уравнений (3.96) дополнялась начальными и граничными условиями (3.91 и 3.92 – 3.95) и решалась методом обыкновенной прогонки попеременно в двух направлениях.
Текст программы алгоритма решения двухмерного параболического дифференциального уравнения (3.2.36), написанной на блочно-структурном языке системы MATH CAD и числовые данные, приведен ниже.
Результаты численных расчетов. Для отработки и выверки выше- приведенного алгоритма численного решения двухмерного уравнения диффузии частиц (3.2.36) ставились два численных эксперимента. В первом эксперименте расчеты концентраций частиц проводились для симметричных условий по обеим координатным осям x и y (число и величины пространственных шагов по осям x и y имели одинаковые значения).
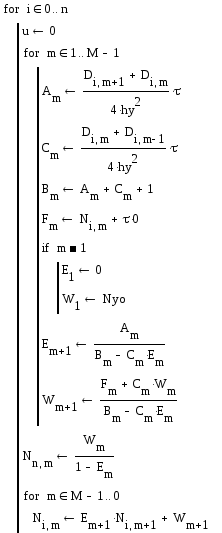
Рассчитанные зависимости концентраций частиц от х и у приведены на рис 2.10.
Рис.3.20. Зависимости концентраций частиц от координат х и у
Как и следовало ожидать, зависимости концентраций частиц от координат x и y, изображенные на рис. 3.20, полностью совпадают, что подтверждает правильность разработанного выше алгоритма численного решения двухмерного уравнения диффузии частиц.
Во втором численном эксперименте число пространственных шагов было одинаковым, а их величины – разными и имели следующие значения:
Xn:=250; n:=50; yM:=50; M:=50; tk:=72000; k:=60; N0:=1; No:=1.2; Nyo:=1.2; Do:=0.4
Для этого случая рассчитанные зависимости концентраций частиц от координат х и у приведены на рис. 3.21.
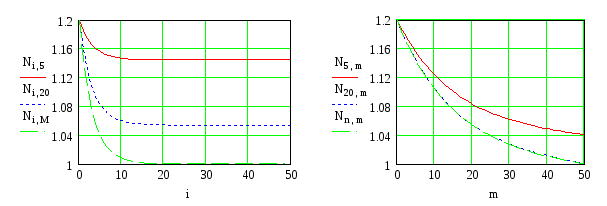
Рис. 3.21. То же самое, что и на рис.3.20, только шаг интегрирования по оси x в пять раз больше, чем по y
Анализ зависимостей концентраций частиц от координат x и y, приведенных на рис.3.21, указывает на разный характер зависимостей N(t,x), так вдоль оси х возмущение, заданное левым краевым условием не успевает добежать до правой границы (большая сторона прямоугольника), то по оси y оно приходит на границу области.
Задание.
Провести численное исследование
процесса
переноса частиц на основе нестационарного
двухмерного дифференциального уравнения
(3.2.36) при следующих начальных и граничных
значениях концентрации
N(x,у,0)
и
N(0,у,t),
N(x,0,t)
(
и
),
а также коэффициентах диффузии D,
приведенных в табл. 3.9.
Таблица 3.9
|
Номер пос-ледней циф-ры зачетной книжки |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
N(x,у,0)10-26м-3 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
|
N(0,у,t) 10-26м-3 |
26.2 |
25.2 |
24.2 |
23.2 |
22.2 |
21.2 |
20.2 |
19.2 |
18.2 |
17.2 |
|
N(x,0,t)10-26м-3 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
|
D,см2/сут |
0.1 |
0.09 |
0.08 |
0.07 |
0.06 |
0.11 |
0.12 |
0.13 |
0.13 |
0.14 |
3.3. Повышение порядка точности аппроксимации дифференциальных уравнений
Как следует из анализа численных экспериментов по решению параболических уравнений по разностным схемам, приведенных выше, погрешность вычислений дискретных значений искомых функций слабо зависит от величины шага интегрирования по времени, что определяется порядком точности аппроксимации этих уравнений 0(τ+h2). В это же время разностные схемы бегущего счета, аппроксимирующие гиперболические уравнения имеют первый порядок точности по обеим переменным t и h, что приводит к необходимости интегрировать эти уравнения с маленькими временными шагами, а это значительно понижает эффективность численных алгоритмов.