Решение систем Нелинейных уравнений методом пРостых итерацй

6.1. Цель работы. Получение практических навыков алгоритмизации и программирования решения систем нелинейных уравнений методом простых итераций.

6.2. Справочный материал. Рассмотрим системы нелинейных уравнений и начальных приближений, записанных в векторной форме

F(x) = 0, x₀ = const. (2.6.1)

явно выразим вектор неизвестных x:

x = f(x). (2.6.2)

Приписывая итерационные индексы вектору неизвестной х в уравнении (2.6.2), таким образом, чтобы справа он был на единицу больше, получаем итерационный вычислительный процесс:

x_i+1 = f(x_i), x₀ = const, i = 0, 1, …, N-1. (2.6.3)

Условия сходимости итерационного процесса для приближений векторных величин

, (2.6.4)

где - малый параметр, определяющий точность вычислений.

Таким образом, итерационный процесс прерывается, при начале выполнения условия сходимости (2.6.4), отсюда и определяется N, как N = i+1.

Второй вопрос решается на основе условия локализации корня. Например, с помощью графика выберем окрестность искомого корня. Эту окрестность называют областью локализации корня. Итерационный процесс (2.6.3) сходится к искомому корню из любой точки области локализации, если в этой области выполняется условие

. (2.6.5)

Приведение исходного уравнения (2.6.1) к итерационному виду (2.6.2) в общем случае неоднозначно. Если для выбранного представления (2.6.2) условие (2.6.5) не выполняется, то нужно искать другую итерационную функцию.

6.3. Пример.

6.3.1. Методом простых итераций с заданной точностью решить систему нелинейных уравнений

(2.6.6)

Преобразуем эту систему уравнений к итерационной форме (2.6.2). Тогда вектор х и вектор правой части f(x) имеют вид

х = ;f(x) = ,

где ;.

Начальные приближения корней возьмем из решения систем нелинейных уравнений (2.6.6) графическим методом:

.

Продифференцируем векторную функцию f(x) по векторному аргументу х, в резултате получим матрицу q(x,y)

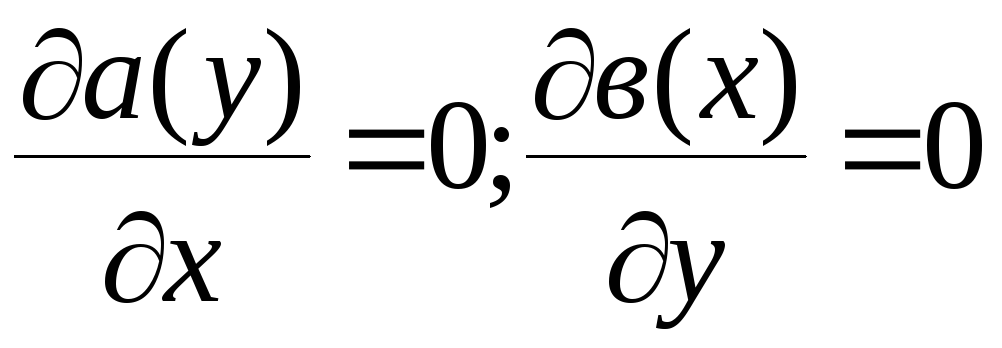, т.к. . (2.6.7)

В качестве нормы матрицы возьмем ее определитель, а т.к. определитель может быть отрицательным необходимо от него еще взять модуль, т.е.

. (2.6.8)

Теперь по формуле (2.6.3) можно построить итерационный процесс.

Рис. 6.1. Развитие итерационного процесса вычисления корней х_к = 3, у_к =0.36

и число итераций, равно N = 1

6.3.2. Методом простых итераций решить систему нелинейных уравнений при начальных приближений корней, значение которых задается из графического метода

x + 3·lg(x) – y² = 0, х₀ = 1.59, у₀ = -1.3, (2.6.9)

2·x² - x·y - 5·x + 1 = 0.

Систему уравнений (2.6.9) запишем в следующем векторном виде:

А(х,у)·Х = ψ(х), Х₀ = const, (2.6.10)

где Х = , А(х,у) = , ψ(х) =.

Пологая, что определитель матрицы А(х,у) не равен нулю (существует обратная матрица А^-1(х,у)), в результате умножения левой и правой части векторного уравнения (2.6.10) на обратную матрицу, получим

Х = f(x,y), где вектор f(x,y) = A^-1(x,y)·ψ(x). (2.6.11)

Теперь по формуле (2.6.3) можно построить итерационный процесс в виде следующего алгоритма.

Программа и результаты итерационных вычислений корней:

Рис.6.2. Развитие итерационного процесса вычисления корней (а) х_к = 1.46

и (b) у_к = - 1.4, при этом, число итераций, равно N = 200

6.4. Задание. Методом простых итераций решить соответствующий вариант задания приведенного в пункте 5.4 предыдущей работы.