3.1.3. Математическая модель стабильности позвоночника

В основу модели положено математическое описание динамических процессов дифференциальными уравнениями Лагранжа 2-го рода, составляемого на основе расчетной схемы трехпозвонкового комплекса, представленного как дискретные сосредоточенные массы, связанные упругодемпфирующими элементами и обладающие определенными геометрическими параметрами [III, 6].

За основу был принят принцип стабильности позвоночного столба изложенный L. Rene, где стабильность позвоночника представлена в вертикальной, горизонтальной и аксиальной плоскостях (ротация), что обеспечивается телами позвонков с дугоотростчатыми суставами, которые связаны между собой упруго-демпфирующими элементами (межпозвоночные диски, мышечно-связочный аппарат).

Учитывались следующие параметры трехпозвонкового комплекса:

1. Механическая система является диссипативной.

2. Распределение нагрузок соответствует трехстолбовой концепции.

3. Предел прочности тел позвонков и упругодемпфирующих элементов, а также их упругая деформация и плотность считались условно установленными по данным работы.

4. Изменение геометрических характеристик трехпозвонкового комплекса соответствовало типичным типам статико-динамических нарушений стабильности позвоночника [III, 6, 13, 21-24].

Расчетная схема фрагмента позвоночника человека, состоящая из трех позвонков с клиновидным средним позвонком и стабилизирующими конструкциями представлена на рис.3.8 с вариантом клиновидной деформации среднего позвонка и двумя стабилизирующими конструкциями (для передних и заднего опорных комплексов).

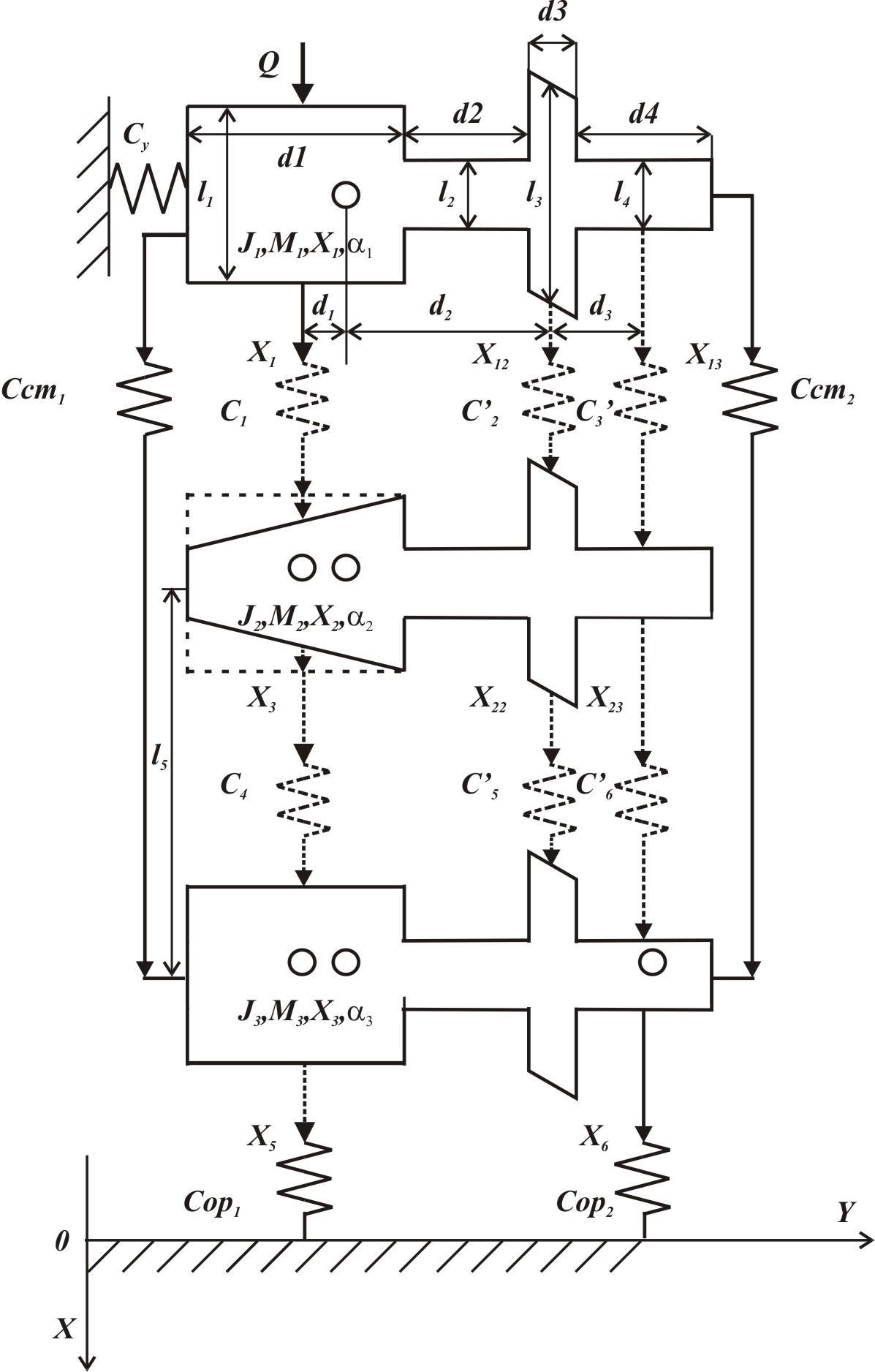
Рис. 3.8. Расчетная схема трехпозвонкового комплекса человека.

Здесь введены следующие обозначения:

J_i, М_i, X_i– момент инерции, масса, координата i-го позвонка (i = 1,2,3);

Cст_i –коэффициенты жесткости j–й стабилизирующей пластины (j = 1,2);

Сop_j - коэффициенты жесткости j–й опоры (j = 1,2);

d1=25 мм; d2=20 мм;d3=5 мм; d4=30 м;

d₁=8.5 мм; d₂=26.5 мм; d₃=17 мм;

l₁=32 мм; l₂=10 мм; l₃=25 мм; l₄=10 мм; l₅=50 мм;

m₁= m₂=m₃ =0.1 кг;

J₁= J₂=J₃=35 кгּмм²; Y_ц=17.2 мм; S=13.25 см².

Координаты Х_ц и Y_ц центра тяжести и момента инерции J плоского позвонка определяются формулами:

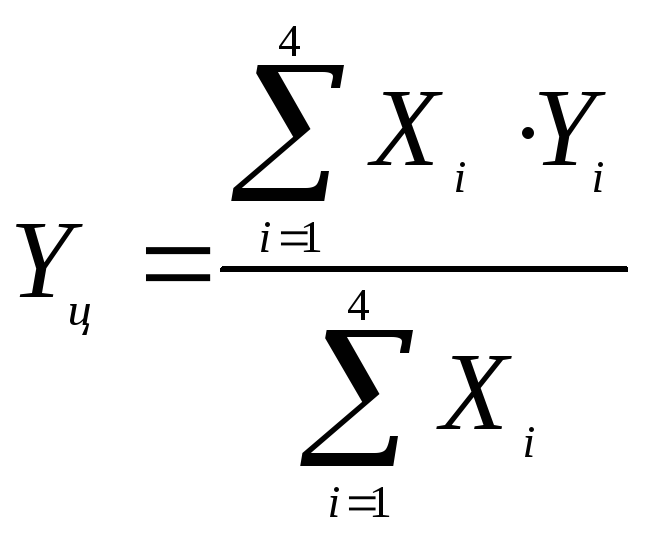; ;(3.1.25)

где индекс i определяет число элементарных фигур, составляющих плоский позвоночник; γ – удельная поверхностная масса позвонка, кг/мм².

Предел прочности, упругая деформация и коэффициенты жесткости различных участков позвоночника по А.П. Громову, приведены в таблице:

Предел прочности, упругая деформация и коэффициенты жесткости различных участков позвоночника Таблица 3.3

Nо.	Наименование комплексов	Предел прочности, кг/см2	Упругая деформация Х, мм	Коэффициенты жесткости С, н/мм
1.	Шейный отдел	120-170	4,0-5,2	(2.30 - 5.52)·103
2.	Грудной отдел	190	5.3	4.66·103
3.	Поясничный отдел	420	5,0-8.5	(6.40-11,00)·103
4.	Целая грудная клетка	240	33,0	944.40

Для упрощения динамической модели трехпозвонкового комплекса коэффициенты жесткости С₂ и С₃, а также коэффициенты жесткости С₅ и С₆ приведены к одним коэффициентам С₂ и С₄ (см. рис.3.8), соответственно, по следующим формулам:

; . (3.1.25)

На расчетной схеме (рис.3.9.) третий позвонок связывается посредством жестких элементов Сор₁ и Сор₂ с опорой по оси Ox, а первый по оси Y через – С_y.

Рис.3.9. Расчетная схема трехпозвонкового комплекса с патологией среднего позвонка и ее двухсторонней стабилизацией (2-ой вариант).

Для фиксации вариантов нестабильности позвоночника предусмотрено применение условных жестких плоскостных конструкций с коэффициентами жесткости Сст₁ и Сст₂, что позволяет моделировать, как жесткие ригидные металлические системы, как и полуригидные пружинные элементы.

Разработанная математическая модель позволяет на основе вычисления внутренних нагрузок опорных комплексов каждого позвонка трехпозвонкового комплекса, рассчитывать варианты переломов и нестабильности позвонков в различных зонах при их патологии. Кроме этого, можно произвести расчет смещения позвонков по оси Oy под воздействием силы Q2_y, что чаще всего является причиной стеноза позвоночного канала и может приводить к удавлению дуального мешка. Выбранная динамическая модель трехпозвонкового комплекса человека (см. рис.3.9.) является механической системой, для которой уравнение Лагранжа II рода имеет вид:

, k=1,…,7, (3.26)

где Т, П – кинетическая и потенциальная энергия системы;

Ф – диссипативная функция, определяемая спинными мышцами;

Q_k – внешние воздействия.

В качестве обобщенных координат X_k принимаются следующие координаты:

х₁; х₂; х₃; х₄ (α₁ = );х₅; х₆ ();у, (3.1.27)

где D_i = d₁ + d₂; i = 1,2,3.

Рис.3.10. К расчету сил, действующих на средний позвонок с патологией трехпозвонкового комплекса человека.

Для вычисления смещающей силы, действующей на 2-й позвонок вдоль оси Y, возникающих вследствие клиновидной деформации (по сути трапеции) второго позвонка рассмотрим рис.3.10.

P₁ Q1₁=Q1·cos(β₁); P₃ O₃=Q3·cos(β₃);

O₁ Q1₂= Q1·sin(β₁); Q₃O₃=Q3·sin(β₃);

Q1_x=O₂ Q1₂=O₁ Q1₂·sin(β₁)= Q1·sin²(β₁);

Q1_y=O₁ O₂= Q1·sin(β₁)·cos(β₁);

Q3_x=O₄ Q3₁·sin(β₃)= Q3·sin²(β₃);

Q3_y=O₃ O₄= Q3·sin(β₃)·cos(β₃);

Q2_y=Q1_y+Q3_y = С₁ Х1·sin(β₁)·cos(β₁)+ С₃ Х3·sin(β₃)·cos(β₃);

y₂= x₁·sin(β₁)·cos(β₁)+ x₃·sin(β₃)·cos(β₃).

Таким образом, проекции сил Q1и Q3 на оси Х и Y при наличии деформации среднего позвонка трехпозвонкового комплекса человека определяются приведенными выше формулами.

Кинетическая энергия механической системы трехпозвонкового комплекса человека, приведенная на рис.3.8. и равна:

(3.1.28)

где ,– квадраты скоростей колебаний и вращений 1-го, 2-го и 3-го позвонков относительно центра тяжестей этих позвонков.

Упругие деформаций х₁, х₂; х₃, х₄; х₅, х₆ центрального и правого столбов 1-го, 2-го и 3-го столбов позвонков связаны с деформаций центра тяжестей этих позвонков X_1, Х₂, Х₃ и α₁, α₂, α₃ следующими соотношениями:

(3.1.29)

Задача решается в приближении малых смещений, то есть

X_i <<D_i; tg(α_i) = sin(α_i) = α_i . (3.1.30)

Тогда X₁ и α₁ выражаются через х₁ и х₂ по формулам (для второго и третьего позвоночника, аналогично):

; X₁ = . (3.1.31)

С учетом соотношения (3.31) кинетическая энергия трехпозвонкого комплекса с патологией среднего позвонка (ТКПСП) и ее двухсторонней стабилизацией, приведенного на рис.2, запишется в следующем виде:

(3.1.32)

где

Потенциальная энергия механической системы трехпозвонкового комплекса человека считается равной нулю при положении статического равновесия (абсолютные координаты), а отсчет деформации упругих элементов ведется от условия, когда статическая нагрузка на элемент уравновешивается упругой силой от его осадки.

В этом случае потенциальная энергия П деформации упругих элементов трехпозвонкого комплекса с патологией среднего позвонка и ее двухсторонней стабилизацией определяется следующим соотношением:

(3.1.33)

Диссипативная функция Ф ТКПСП и ее двухсторонней стабилизацией записывается через коэффициенты демпфирования В_j, как

(3.1.34)

Определив функции кинетической Т, потенциальной энергии П и диссипативных сил Ф, вычислим сначала производные от кинетической энергии по :

(3.1.35)

Производные от потенциальной энергии П трехпозвонкого комплекса по координатам равны:

(3.1.36)

Производные от диссипативный функции Ф трехпозвонкого комплекса:

(3.1.37)

Подставляя значения производных от кинетической и потенциальной энергии, а также от диссипативной функции Ф для механической системы трехпозвонкового комплекса в уравнения Лагранжа II рода, получим:

(3.1.38)

где с₁= cos(β₁); c₃= cos(β₃).

С целью упрощения записи матриц, введем обозначения

S₁= С₁ x₁·sin(β₁)·cos(β₁);

S₃=С₃·x₃·sin(β₃)·cos(β₃);

;

;

;

,

Подставляя значения производных от кинетической и потенциальной энергии, а также от диссипативной функции Ф для механической системы трехпозвонкового комплекса в уравнения Лагранжа II рода, получим в векторном виде:

, (3.1.39)

где

;

Х=

где с₁= cos(β₁); c₃= cos(β₃).

S₁= С₁ x₁·sin(β₁)·cos(β₁);

S₃=С₃·x₃·sin(β₃)·cos(β₃);

;

;

;

,

SB₁= B₁ x₁·sin(β₁)·cos(β₁);

SB₃= B₃ x₃·sin(β₃)·cos(β₃).

Умножая обе части векторного уравнения (3.1.40) на обратную матрицу М^-1, получим следующее приведенное векторное уравнение:

или

, (3.1.40)

где А = М^-1 С; ;F = .

Интерпретация полученных результатов. Для получения эпюр нагрузок Р₁, Р₂ и Р₃, Р₄, а также упругих деформаций х₁, х₂ и х₃, х₄ вдоль оси Y для 1 и 2-го позвонков использовалась линейная интерполяция и экстраполяция в соответствии со следующими формулами (для 1-го позвонка при его длине 80мм)

y, (3.1.41)

где .

Эпюры нагрузок Р₃, Р₄ и упругих деформаций х₃, х₄ для 2-го позвонка рассчитываются по формулам, формулам (3.1.42).

Текст программы алгоритма математической модели трехпозвонкового комплекса, написанной на блочно-структурном языке системы MATH CAD и числовые данные, приведены ниже.

С₁=3.26 10³; С₂=0.92 10³; С₃=0.46 10³; С₄=3.26 10³; С₅=0.92 10³;

С₆=0.46 10³н/мм; С_у=5 10³н/мм; Cop₁=Cop₂=3.26 10³н/мм;

Q=400кг (внешняя сила приложена к центру тяжести позвонка при у=21мм); β₁=0⁰; β₃=0⁰ (деформация позвонка отсутствует); Сст₁=Сст₂=0 (стабилизирующие пластины слева и справа от позвонков отсутствуют (см. рис.3.11)), число временных слоев j = 1000, а шаг интегрирования по времени τ = 10^-2с.