Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие

приведена к виду

71

верно. Аналогично можно проверить, что AA−1 = E .

§ 2.6. ОБРАЩЕННЫЙ БАЗИС СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Пусть дана система k линейных алгебраических уравнений с n неизвестными (2.3.1).

Исследуем ее, вычислив ранги матрицы системы и расширенной матрицы с помощью миноров. Предположим, что она оказалась совместной, все уравнения линейно независимы и пусть, для определенности, ненулевой минор Mk наивысшего порядка k (базисный минор) порождает-

ся подматрицей

составленной из коэффициентов при первых m неизвестных. Для матрицы Qk найдем обратную матрицу

Матрицу Q−k 1 называют обращенным базисом.

Запишем систему уравнений (2.3.1) в матричной форме и умножим обе части слева на матрицу Q−k 1 :

72

gij = ui1a1 j + ui 2a2 j + …+ uik akj , hi = ui1b1 + ui 2b2 + …+ uik bk

или

Тогда равенство (2.6.1) можно переписать в виде

или

Мы пришли к предпочитаемому эквиваленту исходной системы линейных алгебраических уравнений. Базисными оказались те неизвестные, из коэффициентов при которых был составлен ненулевой минор наивысшего порядка при исследовании системы. Особо подчеркнем, что матри- цы-столбцы коэффициентов при неизвестных и свободных членов в исходной и предпочитаемой формах системы связаны соотношениями

Из (2.6.2) получаем для исходной системы общее решение

73

И еще одно важное замечание. Пусть a j — вектор-столбец, компонентами которого являются коэффициенты при неизвестной x j в системе

уравнений (2.3.1), а b — вектор-столбец правых частей уравнений той же системы. В силу предположения векторы a1,a2 ,…,ak образуют базис си-

стемы векторов a1,a2 ,…,ak , ak +1,ak +2 ,…,an ,b . Пусть g j — вектор-столбец коэффициентов при неизвестной x j в предпочитаемой форме системы

уравнений, а h — столбец свободных членов. Тогда можно доказать, что координаты векторов g j и h являются коэффициенты разложения векторов

соответственно a j и b по базисным векторам a1,a2 ,…,ak :

a j = g1 ja1 + g2 ja2 + + gkjak , j = 1, 2, …, n, b = h1a1 + h2a2 + + hmam .

§ 2.7. МОДЕЛЬ МЕЖОТРАСЛЕВОГО БАЛАНСА

Идеи модели межотраслевого баланса, рассматриваемой в данном разделе, впервые возникли в 1920-х гг. в работах экономистов молодой Советской России, которые строили модель плановой экономики, удовлетворяющей спрос конечных потребителей. Наибольшее развитие эти идеи получили в трудах В. Леонтьева, эмигрировавшего к тому времени в США. В 1973 г. за эти исследования В. Леонтьеву была присуждена Нобелевская премия в области экономики.

Пусть производственный сектор национальной экономики разделен на n ч и с т ы х о т р а с л е й (например, «машиностроение», «энергетика», «транспорт» и т. д.), каждая отрасль производит один вид продукции, различные отрасли выпускают разную продукцию. В процессе производства каждая отрасль может расходовать как свою продукцию, так и про-

74

дукцию других отраслей, поэтому на непроизводственное потребление, вообще говоря, идет не вся выпущенная продукция (часть ее тратится в процессе производства).

Введем обозначения: aij — количество продукции i-й отрасли, расходуемое в процессе производства единицы продукции j-й отрасли, xi — план выпуска i-й отрасли, ci — спрос на продукцию i-й отрасли в непроизводственной сфере.

Матрица A = (aij) называется матрицей прямых затрат. Если считать сложившиеся производственные технологии н е и з м е н н ы м и в о в р е м е н и, то матрица A будет постоянной.

Кроме того, будем считать технологии л и н е й н ы м и: если для выпуска единицы продукции j-й отрасли необходимо израсходовать aij единиц продукции i-й отрасли, то для выпуска xj единиц продукции j-й отрасли необходимо израсходовать aijxj единиц продукции i-й отрасли.

В этих предположениях объем продукции i-й отрасли, потребляемый всеми n отраслями в процессе производства, равен

n

∑aij x j , j =1

поэтому на конечное непроизводственное потребление остается

n

xi − ∑aij x j j =1

единиц продукции i-й отрасли.

Значит, чтобы конечный спрос был обеспечен, необходимо выполнение б а л а н с о в ы х р а в е н с т в

n

xi − ∑aij x j = сi , i =1, 2, …, n .

j =1

75

вектор конечного непроизводственного потребления,

единичная матрица.

Из матричной формы модели Леонтьева

(E − A )x = c

можно выразить зависимость вектора валового выпуска x от вектора конечного непроизводственного потребления y:

x = (E − A)−1c ,

матрица (E − A)−1 называется при этом матрицей полных затрат.

Модель Леонтьева называется продуктивной, если она разрешима в неотрицательных x.

ПРИМЕР 2.7.1. В модели Леонтьева даны матрица прямых затрат

и вектор конечного спроса

c= 3 .

2

Требуется найти вектор x валового выпуска, обеспечивающий данный

спрос.

Решение. Найдем матрицу полных затрат (E – A)–1 :

76

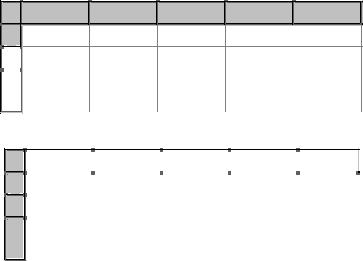
Теперь поясним, как получить тот же результат в пакете Microsoft Excel. Введем матрицу (E – A) в ячейки A2:C3 рабочего листа Microsoft Excel, как показано на рис. 3.2.1, а.

Матрица (E – A)–1 имеет две строки и два столбца, отведем под результат ячейки D2:E3. В ячейку D2 введем формулу «=МОБР(A2:B3)», причем эту формулу необходимо ввести как ф о р м у л у м а с с и в а. Для этого нужно мышью выделить диапазон D2:E3, начиная с ячейки D2, содержащей формулу, затем нажать клавишу <F2>, а затем — комбинацию клавиш <Ctrl> + <Shift> + <Enter>. Результат представлен на рис. 3.2.1, б (в ячейках D2:E3). Замечаем, что результаты ручного и компьютерного вычисления обратной матрицы совпали. Если формулу ввести не как формулу массива, то будет рассчитан только левый верхний элемент результата: число 3.

а) формула Microsoft Excel

Рис. 3.2.1. Вычисление матрицы полных затрат с помощью Microsoft Excel

Таким образом, матрица полных затрат

Теперь можно найти вектор валового выпуска, обеспечивающий

77

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1.Приведите примеры векторов и матриц из экономической практики.

2. Даны векторы a = (15, –12, 2) и b = (8, 16, 24). Найдите 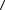a + b, a − b ,

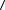2a + 3b, − a + 2b .

Найдите матрицы AB, cd, dc, BE − AT , если они существуют.

4.Найдите AB – BA и CD – DC, если

5.Найдите ранги матриц из задач 3 и 4.

6.Исследуйте данные системы линейных уравнений методом последовательного исключения неизвестных и в случае совместности найдите общее решение, не менее двух базисных решений и какоенибудь одно частное небазисное решение:

7.Найдите не менее двух базисных неотрицательных решений для каждой из систем, представленных в задаче 6.

8.Для данных матриц найдите обратные или докажите необратимость:

78

ГЛАВА 3. МЕТОДЫЛИНЕЙНОГОПРОГРАММИРОВАНИЯ

§ 3.1. ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему линейных алгебраических уравнений или неравенств и среди всех неотрицательных решений найти то решение, при котором линейная функция принимает наибольшее или наименьшее значение. Изучение методов исследования и решения математических задач указанного типа составляет содержание раздела математики, который называется линейным программированием.

Основная задача линейного программирования выглядит сле-

дующим образом.

Дана система m линейных уравнений с n неизвестными:

где все неизвестные могут принимать только неотрицательные значения:

называемая ц е л е в о й ф у н к ц и е й.

Требуется среди всех решений системы уравнений (3.1.1) найти такое неотрицательное решение, при котором целевая функция (3.1.3)

принимает наибольшее возможное значение.

Любое неотрицательное решение системы уравнений (3.1.1) называют допустимым решением, а то допустимое решение, при котором целевая функция (3.1.3) принимает наименьшее значение, называют оптимальным

79

решением задачи линейного программирования (3.1.1)—(3.1.3). Кратко задачу формулируют так: найти вектор (x1, x2 , …, xn ) , минимизирующий целе-

вую функцию (3.1.3) при линейных ограничениях (3.1.1) и (3.1.2).

Мы остановились на вполне определенной формулировке основной задачи линейного программирования, имея в виду, что если в математической модели какой-либо конкретной задачи планирования будут содержаться линейные неравенства, то их можно заменить линейными уравнениями с помощью дополнительных неотрицательных неизвестных. Кроме того, если в конкретной задаче будет необходимо найти наименьшее возможное значение некоторой линейной функции u = c1 x1 + c2 x2 +…+ c n xn при линейных

ограничениях, то для приведения такой задачи к принятому нами виду основной задачи линейного программирования достаточно линейную функцию u заменить противоположной ей функцией v = −c1 x1 − c2 x2 −…− c n xn ,

так как если функция v принимает набольшее значение при некоторых значениях переменных, то при тех же значениях переменных функция u примет наименьшее возможное значение.

Может случиться также, что в математической модели конкретной задачи некоторые переменные по своему содержательному смыслу могут принимать и отрицательные значения. Тогда для каждой такой переменной

функции, после чего задача приводится к стандартному виду.

Не всегда удобно пользоваться формулировкой задачи линейного программирования (3.1.1)—(3.1.3). В частности, вместо системы линейных уравнений (3.1.1) целесообразно иногда иметь систему линейных неравенств. Чтобы перейти от системы линейных уравнений к системе линейных неравенств, достаточно заметить, что уравнение

ai1 x1 + ai 2 x2 +…+ ain xn = bi

равносильно системе двух неравенств:

ai1 x1 + ai 2 x2 +…+ ain xn bi ,ai1 x1 + ai 2 x2 +…+ ain xn bi .

С другой стороны, если в математической модели конкретной задачи условия, которыми связаны переменные целевой функции, представляют собой систему линейных алгебраических неравенств, то ее можно заменить некоторой системой линейных алгебраических уравнений с бó льшим числом неизвестных и привести задачу к принятому нами виду основной задачи линейного программирования.

Поэтому задачу линейного программирования нередко формулируют как задачу минимизации или максимизации линейной функции (3.1.3) при ограничениях

80