Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новокузнецкий институт (филиал КемГУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие

.pdf

Скачиваний:

1245

Добавлен:

19.04.2015

Размер:

6.01 Mб

Скачать

☆

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 3720 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

§ 6.3. МОДЕЛЬПОВЕДЕНИЯ ПОТРЕБИТЕЛЯ

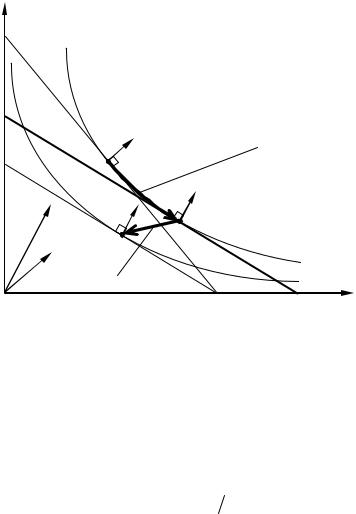
Теперь сформулируем математически задачу потребителя: требу-

ется из бюджетного множества выбрать набор товаров, обладающий максимальной полезностью:

u(x) → max, x B.

Запишем эту задачу подробнее [с учетом (3.1.1)]:

u(x1, x2 , …, xn ) → max,
p1x1 + p2 x2 + + pn xn I ,	(6.3.1)

x1 0, x2 0, …, xn 0.
ТЕОРЕМА СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ РЕШЕНИЯ ЗАДАЧИ ПОТРЕБИТЕ-
ЛЯ. Решение

x1x2

задачи потребителя (6.3.1) существует, лежит на границе бюджетного множества:

p x + p		x + + p		x = I	(6.3.2)
1 1	2	2	n	n

и если функция полезности является строго выпуклой вверх, то решение задачи потребителя (6.3.1) является единственным.

Доказательство. Существование решения следует непосредственно из теоремы Вейерштрасса (о том, что непрерывная функция достигает на замкнутом ограниченном множестве максимального и минимального значения.

Условие (6.3.2) докажем от противного. Предположим, что в точке x максимума функции полезности выполняется неравенство

p1 x1 + p2 x2 + + pn xn < I .

Тогда на остаток бюджета I − p1x1 + p2 x2 + + pn xn можно приобрести некоторый набор товаров a , причем хотя бы одна из координат ai > 0 Пусть y = x + a , тогда y B и в силу аксиомы о том, что каждый товар является для потребителя желательным, u(y ) > u(x ) , что противоречит предположению, что x — точка максимума функции полезности на бюджетном множестве.

Теперь докажем единственность решения задачи потребителя. Пусть существуют две точки максимума: x(1) и x( 2) . Тогда u (x(1) ) = u (x(2) ), при этом в силу условия (6.3.2)

191

p x(1)	+ p	x(1)	+ + p	x(1)		= I ,
1 1	2	2	n		n
p z( 2) + p		z( 2)	+ + p		z( 2) = I.
1 1	2	2	n		n

Рассмотрим точку x(3) = 12 (x(1) + z(2) ) . В этой точке, очевидно,

p1x1(3) + p2 x2(3) + + pn xn(3) = I ,

а поскольку по условию теоремы функция полезности строго выпукла вверх,

u (x(3) ) = u ( 12 (x(1) + x( 2) )) > 12 (u (x(1) ) + u (x( 2) )) = u (x(1) ) = u (x( 2) ) ,

что входит в противоречие с предположением о том, что x(1) и x( 2) — точки максимума.

Перепишем задачу (6.3.1) в виде общей задачи выпуклого программирования:

u(x1, x2 , …, xn ) → max,

p1x1 + p2 x2 + + pn xn I ,
−x				0,
	1			(6.3.3)
	−x2			(6.3.3)
	−x2			0,


		−x	n	0,
			n

введем вектор множителей Лагранжа

y = (λ y1 y2 … yn ),

первая координата которого λ соответствует бюджетному ограничению p1x1 + p2 x2 + + pn xn I , а оставшиеся координаты y1, y2 ,…, yn — огра-

ничениям неотрицательности спроса x1 0, x2 0, …, xn 0,									составим для
задачи (6.3.3) функцию Лагранжа
		L(x1, x2 , …, xn , λ, y1, y2 , …, yn ) =
= u(x1, x2 , …, xn ) + λ ( I − p1x1 − p2 x2 − − pn xn )								m
= u(x1, x2 , …, xn ) + λ ( I − p1x1 − p2 x2 − − pn xn )								+ ∑ yi xi ,
								i=1
и запишем для этой задачи условия Каруша —							Куна —	Таккера (3.2.3)—
(3.2.6):
	∂L	=	∂u	− λp j	+ y j = 0,	j = 1, 2, …, n ,			(6.3.4)
		=		− λp j	+ y j = 0,	j = 1, 2, …, n ,			(6.3.4)
	∂x j		∂x j
	∂L		= I − p x − p x − − p x 0 ,
	∂λ		1 1		2 2	n	n
			1 1		2 2	n	n

192

∂L

= x j 0,

j = 1, 2, …, n ,

∂y j

λ ∂L = λ (I − p x − p x − − p x

) = 0 ,

∂λ

1 1

2 2

∂L

= y

= 0,

j = 1, 2, …, n ,

∂y

λ 0,

y j 0,

j = 1, 2, …, n .

Выразив из (6.3.4)

y j = λ p j

−

∂u

j = 1, 2, …, n ,

∂x j

перепишем остальные условия с учетом (6.3.2):

λ 0,

∑ p j x j

= I ,

(6.3.5)

j=1

∂u

λ p

∂u

− λ p

= 0,

j = 1, 2, …, n . (6.3.6)

∂x

Условия (6.3.6) означают, что в оптимальной точке возможны два варианта: либо j-й товар потребляется в ненулевом количестве, и тогда

∂u	= λ p j ,	(6.3.7)

∂x j

либо ∂u / ∂x j < λp j , и тогда j-й товар не потребляется. Отсюда следует

очень важное свойство решения задачи потребителя: если в оптимальной точке i-й и j-й товары потребляются в ненулевом количестве, то предельная норма замены i-го товара j-м равна отношению цен i-го и j-го товаров:

r j =	∂u / ∂xi	=	pi	.	(6.3.8)
	∂u / ∂x j
i			p j

Равенство (6.3.8) можно содержательно интерпретировать в виде второго закона Госсена: взаимозаменяемыми являются такие количества товаров, которые имеют одинаковую стоимость.

Кроме того, условия (6.3.6) означают и то, что вектор предельных полезностей потребляемых (в н е н у л е в о м к о л и ч е с т в е) товаров пропорционален вектору цен:

193


∂u	:	∂u	:…:	∂u	= p : p :…: p .		(6.3.9)

∂x1		∂x2		∂xn		n
				1 2

Можно сделать еще один вывод из условий (6.3.6): у всех потребляемых (в н е н у л е в о м к о л и ч е с т в е) товаров в оптимальной точке отношения предельных полезностей к ценам совпадают и равны λ :


	∂u / ∂x1	=	∂u / ∂x2	= =	∂u / ∂xn		= λ .	(6.3.10)

	p1		p2			pn
Это дает ответ на вопрос об экономическом смысле множителя
Лагранжа λ : множитель Лагранжа равен						п р е д е л ь н о й		п о л е з н о -
с т и о д н о й д е н е ж н о й			е д и н и ц ы			(поскольку в оптимальной точ-

ке часть предельной полезности каждого товара, приходящаяся на единицу

его цены, равна λ ).
	Важно заметить, что для тех товаров, которые в оптимальной точке
не потребляются, условия (6.3.8)—(6.3.10) не выполняются.
	Если из условий (6.3.4) выразить x как функцию от цен и богат-
ства,	то	получим		функцию	спроса	данного	потребителя:
x = x ( p , p		, …, p	, I ) .
	1 2	n

В параграфе 3.1 отмечалось, что при одновременном увеличении в k раз цен всех товаров и богатства потребителя бюджетное множество не изменяется, поэтому, очевидно,

x (kp , kp	2	, …, kp	n	, kI ) = x ( p , p	2	, …, p	n	, I ) ;	(6.3.11)
1	2		n	1	2		n

ТЕОРЕМА О ДИФФЕРЕНЦИАЛЬНЫХ СВОЙСТВАХ ФУНКЦИИ СПРОСА. Если реше-

ние задачи потребителя (6.3.1) дифференцируемо, то пропорциональное изменение всех цен и доходов не влияет на спрос:

n		( p1, p2 , …, pn	, I )			( p1, p2 , …, pn	, I )
∑ pi	∂x j			+ I	∂x j			= 0 ;	(6.3.12)
		∂pi				∂I
i=1

изменение цены одного товара не влияет на общие расходы:

n	∂x	( p , p , …, p , I )		+ x j ( p1, p2 , …, pn , I ) = 0 ;	(6.3.13)
∑ pi	i	1 2	n	+ x j ( p1, p2 , …, pn , I ) = 0 ;	(6.3.13)
i=1		∂p j

изменение дохода влечет соответствующее изменение суммарных расходов

n	∂x	( p , p ,…, p , I )
∑ pi	i	1 2	n	= 1;	(6.3.14)
		∂I
i=1
Доказательство. Условие (6.3.12) получается дифференцированием
по k равенства (6.3.11), а условия (6.3.13) и (6.3.14) —					дифференцированием
соответственно по p j и по I равенства (6.3.2).

194

ПРИМЕР 6.3.1. В условиях примера 6.1.1 известна также функция полезности потребителя u(x1, x2 , x3 ) = x1x2 x3 . Требуется определить

функцию спроса и рассчитать ее конкретное значение при заданном богатстве I и векторе цен p.

Решение. Предельные полезности товаров в данном примере равны

∂u

x2 x2

∂u

x1x3

∂u

x1x2

∂x1

2 x1

∂x2

2 x2

∂x3

2 x3

В оптимальном решении

задачи потребителя x1 ¹ 0, x2 ¹ 0, x3 ¹ 0,

так как

u(x1, x2 , 0) = u(x1, 0, x3 ) = u(0, x2 , x3 ) = 0 .

Поэтому условия

(3.2.2),

(3.2.7) для определения функции спроса принимают вид

x2 x3

¶u

x2 x3

= lp1,

x1 =

¶x1

2 x1

2lp1

¶u

x2 x3

x x

¶x2

= lp2 ,

2 x2

= lp2 ,

Û 2 x2

2lp1

¶u

= lp ,

x1x2

x2 x3

¶x

= lp3 ,

2lp

= lp3 ,

+ p x

= I

p1x1 + p2 x2 + p3 x3 = I

p x + p x + p x = I

p x + p x

1 1

2 2

3 3

1 1

2 2

3 3

x =

x2 x3

( p ,

p ,

I ) =

3 p1

4λ2 p12

x1 = 4λ

p2 p3 ,

( p , p , p , I ) =

= λp2

4λ

3 p2

p1 p2 ,

4λp

= 4λ2 p1 p3 ,

( p , p , p , I ) =

= λp3

3 p3

4λp1

12λ

p1 p2 p3 = I

p x + p x + p x = I

12 p1 p2 p3

Таким образом, функция спроса данного потребителя

I / (3 p1)

x ( p , p , p , I ) = I / (3 p )

(6.3.15)

I / (3 p3 )

а предельная полезность денег

l =

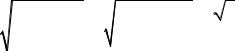
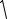12 p1 p2 p3

195

При данном векторе цен p = (2 5

6) и богатстве I = 30 получаем:

x ( p ,

p , I ) =

= 5,

( p

, p

p , I ) =

= 2,

3 p1

3 × 2

3 p2

3 × 5

( p

, p

, p , I ) =

l =

3 p3

3 × 6 3

12 p1 p2 p3

12 × 2 ×5 × 6 12

Итак, вектор спроса при данных ценах и данном богатстве таков:

		5
x	=	2	.
x	=	2	.

		5 / 3

§ 6.4. УРАВНЕНИЕ СЛУЦКОГО

Рассмотрим, как изменится спрос потребителя, если изменится цена одного из товаров (например, j-го).

Предположим вначале, что при изменении цены j-го товара на ве-

личину Dp j (при	неизменных	ценах остальных	товаров) происходит
к о м п е н с а ц и я	б о г а т с т в а	на такую величину	I , чтобы новая точ-

ка оптимального спроса осталась на той же поверхности безразличия, что и старая [иными словами, чтобы полезность набора товаров

x′ = x ( p , p ,…, p

+ p

,…, p , I + I ) ,

оптимального при векторе цен P =(p1

pj +Δpj

pn )

и богат-

стве I + I , была бы равна полезности набора товаров

x = x ( p , p ,…, p

,…, p , I ) ,

оптимального при векторе цен p = ( p1

p j

pn ) и богатстве I

(рис. 6.4.2)].

Если теперь устремить Dp j

к нулю и рассмотреть предел

lim

x′ − x

i i

p j

→0,

p j

→0,

u (x′)=u (x )

( p , p , …, p

, …, p

, I +

I ) − x

( p , p , …, p

, …, p , I )

lim

1 2

p j

p j →0,

u (x′)=u (x )

то мы получим изменение спроса на i-й товар при изменении цены j-го товара на единицу и сопутствующем компенсирующем изменении богатства; это изменение обозначается


¶xi	=	lim		Dxi	.

¶p j комп.		p j →0,	)	Dp j
		u ( x′)=u ( x

196

I +ΔI

	p′=(p , p +dp )
1		2	2
I +ΔI

p2 +Δp2		gradu(x ) p
	x

gradu(x′) p′

p′	x′

p	x2

0	I	I +ΔI

	p1	p1
Рис. 6.4.2. Изменение спроса с компенсацией дохода

Величина (¶x	/ ¶p	)	комп.	отражает э ф ф е к т з а м е щ е н и я — при
i	j		комп.

изменении цены j-го товара и компенсирующем изменении богатства потребитель останется на той же поверхности безразличия, что и раньше, для чего заменит часть j-го товара другими товарами.

Найдем величину такого компенсирующего изменения богатства dI при бесконечно малом изменении цены j-го товара (на dpj) и неизменных остальных ценах [т. е при изменении цен pi всех остальных товаров (с номерами k ¹ j ) на dpk = 0 ].

Из условий оптимального поведения потребителя (3.2.4) получаем,

что

n	¶u		n	n	n
du = ∑	¶u	dxk = l ∑ pk dxk ,		dI = ∑ pk dxk + ∑xk dpk .
du = ∑		dxk = l ∑ pk dxk ,		dI = ∑ pk dxk + ∑xk dpk .
k =1	k		=	=	=
	¶x		k 1	k 1	k 1
Чтобы полезность не изменилась, необходимо и достаточно, чтобы
du = 0 , и поскольку предельная полезность денег l ¹ 0 , то
			n
			∑ pk dxk	= 0 .
			k =1
Но тогда
		n	n	n	= x j dp j
d I = ∑ pk dxk + ∑ xk dpk				= ∑ xk dpk	= x j dp j	(6.4.1)
		k =1	k =1	k =1
(где мы учли также, что dpk			= 0 при k ¹ j ).

На самом деле компенсации богатства потребителя при изменении цен не происходит, и изменение спроса потребителя на i-й товар при изменении цены j-го товара на единицу равно

197

∂x		∂x		∂x
i	=	i	−	i x j ,	i = 1, 2, …, n,	j = 1, 2, …, n .	(6.4.2)
∂p j
		∂p j комп.		∂I

Уравнение (6.4.2), полученное в 1915 г. Е. Е. Слуцким, играет важнейшую роль в теории потребительского спроса. Вычитаемое в этом уравнении отражает э ф ф е к т д о х о д а, связанный с изменением потребительской ценности единицы богатства. Фактически потребитель не остается на той же поверхности безразличия, что и раньше, а переходит на другую поверхность безразличия, соответствующую другим количествам товаров, которые он может позволить себе приобрести при изменении цены j-го товара и неизменном богатстве и ценах остальных товаров. Эффект дохода и эффект замещения иллюстрируется рис. 6.4.3.

		x2
	I
	p2
			p′=(p , p +dp )
			1	2	2
I +ΔI

p2 +Δp2				gradu(x ) p			эффект
			x′′	gradu(x ) p			эффект
I							замещения
p2 +Δp2					gradu(x′) p′
					gradu(x′) p′
		p′			x′
		p′
			p′
		p	эффект дохода						x1
			эффект дохода						x1
0						I		I +ΔI

						p1		p1

Рис. 6.4.3. Эффект дохода и эффект замещения

ПРИМЕР 6.4.1. В условиях примера 6.3.1 требуется убедиться в

справедливости уравнения Слуцкого для данного потребителя.

Решение. Рассмотрим, например, что произойдет со спросом при изменении цены первого товара. Пусть цена первого товара изменилась с p1 до p1 + p1 . Если произошло соответствующее компенсирующее изме-

нение богатства на величину			I = x	p = I	p		3 p		[определенную по фор-
			1	1		1	1
муле (6.4.1)], то новая точка спроса								I +
								I +	I

						3( p +			p )
							1		1
x ( p + p , p , p , I + I ) =								I + I		,
x ( p + p , p , p , I + I ) =										,
1	1	2	3					3 p2
1	1	2	3

								I +	I
								I +	I
								3 p3
								3 p3

198

т. е. изменение спроса составляет

x = x ( p + p , p , p , I + I ) − x

( p , p , p , I ) =

I + I

−

(I + I ) p1 − I ( p1 +

p1 )

p1 I − I p1

3( p +

3 p

( p +

p )

3 p

( p +

p )

p ) 3 p

I + I

−

3 p2

I + I − I

3 p

Подставим сюда

I = I

p1 / (3 p1) , получим

p1I p1 / (3 p1 ) − I p1

−2I p1

3 p ( p + p )

9 p ( p +

p )

1 1

x =

9 p1 p2

9 p1 p3

Отсюда находим изменение спроса при бесконечно малом изменении цены первого товара и компенсирующем изменении дохода:

∂x

−2I p1

−2I

9 p ( p + p )

lim

1 =

lim

1 1

lim

= −

∂p

9 p

( p +

9 p

комп.

p1→0,

p1 →0,

p1→0,

p )

)

u (x′)=u (x )

u (x′)=u (x

∂x
	2
	∂p
	1	комп.
∂x
	3
	∂p
	1	комп.

=	lim
	p1→0,
	u (x′)=u (x )
=	lim
	p1→0,
	u (x′)=u (x )

x2 p1

x3 p1

=	lim
	p1 →0,
	u (x′)=u (x )
=	lim
	p1 →0,
	u (x′)=u (x )

9 p1 p2

lim

p1 →0,

9 p p 9 p p

u (x′)=u (x )

1 2

9 p1 p3

lim

p1→0,

9 p p 9 p p

u (x′)=u (x )

1 3

∂x1 ∂p1

∂x1 ∂I

Найдем теперь ∂x	/ ∂p ,	∂x	/ ∂I (i = 1, 2, 3):
i	1	i

∂[I / (3 p )]

∂x

∂[I / (3 p

)]

∂x

∂[I / (3 p

)]

= −

2 =

= 0,

3 =

= 0,

∂p

3 p2

∂p

∂[I / (3 p )]

∂x

∂[I / (3 p )]

∂x

∂[I / (3 p )]

2 =

3 =

∂I

3 p

∂I

3 p

∂I

3 p

Замечаем, что

199

∂x

1 I

∂x

−

1 x = −

−

= −

1 ,

∂p

9 p2

3 p

3 p2

∂I

3 p

∂p

комп.

∂x

−

2 x =

−

= 0

2 ,

∂p

9 p p

3 p

∂I

∂p

комп.

∂x

1 I

∂x

−

3 x =

−

= 0

3 ,

∂p

9 p p

3 p

∂I

∂p

комп.

т. е. уравнение Слуцкого (6.4.2) для данного потребителя действительно выполняется.

Можно показать, что

∂x		< 0 ,	(6.4.3)
	i
	∂p
	i комп.

т. е. при увеличении цены (i-го) товара, сопровождающемся компенсирующим изменением богатства, спрос на данный товар падает.

Товар с номером i называется ценным, если при увеличении богатства спрос на него растет, т. е. если

∂x	(6.4.4)
i > 0,	(6.4.4)
∂I

и малоценным, если при увеличении богатства спрос на этот товар снижается:

∂xi < 0 . ∂I

В оптимальной точке [согласно (3.2.4)]

∑ pk xk = I .

k =1

Продифференцируем левую и правую части этого равенства по I:

n	∂x	= 1.
∑ pk	k
k =1	∂I
Отсюда (с учетом того, что все		pk > 0 ) следует, что среди частных
производных ∂x / ∂I есть хотя бы одна положительная, т. е. обязательно
k
существует хотя бы один ценный товар.
Товар с номером i называется нормальным, если при увеличении
его цены спрос на него падает, т. е. если
∂x
i	< 0 ,
∂pi

200

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 1920 / 3720 21 22 23 24 25 26 27 28 29 30 31 32 > Следующая >>>

Соседние файлы в папке Семестровая 1 (Методы оптимальных решений)

#
19.04.201553.55 Кб144(Методы оптимальных решений) Семестровая 1.docx
#
19.04.20156.01 Mб1245Методы оптимальных решений учебное пособие.pdf
#
19.04.2015177.31 Кб404Пример решения задачи симплекс методом..docx
#
19.04.201562.74 Кб72Пример решения ЗЛП графическим методом и анализ чувствительности модели.docx