
Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие
.pdf
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а |
4.1.2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потребление |
b1 = 41 |
b2 = 50 |
b3 = 44 |
b4 = 30 |
b5 = 12 |
|
|
||||||||
Производство |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 |
|
|
3 |
|
2 |
|
0 |
|
|
a1 = 54 |
41 |
|
13 |
|
|
|
|
|
|
|
|
|
p1 = 0 |
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
3 |
|
|
6 |
|
|
2 |
|
5 |
|
0 |
|
|
a2 = 60 |
|
|
|
|
37 |
|
23 |
|
|
|
|
|
|
p2 = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
+ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
5 |
|
|
6 |
|
7 |
|
0 |
|
|
|
a3 = 63 |
|
* |
|
|
|
|
|
21 |
|
30 |
|
12 |
|
|
p3 = 6 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
– |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||||
|
q1 = 1 |
q2 = 4 |
q3 = 0 |
q4 = 1 |
q5 = –6 |
|
|
||||||||
Положим p1 = 0 |
и найдем остальные потенциалы из условия, |
что |
|||||||||||||
для базисных клеток ij |
= 0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 = 0, p1 + q1 − c11 = 0, 0 + q1 −1 = 0, q1 = 1, 12 = 0, p1 + q2 − c12 = 0, 0 + q2 − 4 = 0, q2 = 4, 22 = 0, p2 + q2 − c22 = 0, p2 + 4 − 6 = 0, p2 = 2,
и т. д. В результате получим: q3 = 0, p3 = 6,q4 =1,q5 = −6 .
Затем по формуле (4.1.6) вычислим оценки всех свободных клеток:
13 = p1 + q3 − c13 = 0 + 0 − 3 = −3, |
14 = p1 + q4 − c14 = 0 + 1− 2 = −1, |
15 = p1 + q5 − c15 = 0 − 6 − 0 = −6, |
21 = p2 + q1 − c21 = 2 + 1 − 3 = 0, |
24 = −2, 25 = −4, |
31 = 5, 32 = 5. |
Находим наибольшую положительную оценку:
max( ij > 0) = 5 = |
31 . |
|
i, j |
|
|
Для найденной свободной клетки (3, 1) построим цикл пересчета: |
||
(3, 1) — (1, 1) — (1, 2) — (2, 2) — (2, 3) — (3, 3 |
). |
|
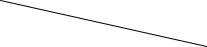
Производим перераспределение поставок вдоль цикла пересчета (на |
||
рис. 4.1.2, а ρmax = 21), получаем второе базисное |
допустимое решение |
|
(табл. 4.1.3).
141
|
41 |
13 |
|
|
|
|
|
|
41 – ρ |
13 + ρ |
|
|
|
|
|
|
|
|
|
20 |
34 |
|
|
|
|
|
|
|||||||
|
|
37 |
23 |
|
→ |
|
|
|
|
37 – ρ |
|
23 + ρ |
|
→ |
|
|
16 |
|
44 |
|
|
|
||||||||||||
|
* |
|
|
21 |
|
|
|
|
|
ρ |
|
|
|
|
21 – ρ |
|
|
|
|
21 |
|
|
|
|
|
|
|
|
||||||
|
|
а) при переходе ко второму базисному решению |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
20 |
|
* |
|
|
→ |
|
20 – ρ |
|
|
|
ρ |
|
→ |
|
|
|
20 |
|
|
|
|
|
|
|
|||||||
|
|
|
21 |
|
30 |
|
|
|
21 + ρ |
30 – ρ |
|
41 |
10 |
|
|
|
|
|
|
|
||||||||||||||
|
|
б) при переходе к третьему базисному решению |
|
|
|
|||||||||||||||||||||||||||||
Рис. 4.1.1. Перераспределение поставок вдоль цикла пересчета |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а |
4.1.3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Потребление |
|
b1 = 41 |
|
b2 = 50 |
|
b3 = 44 |
b4 = 30 |
|
b5 = 12 |
|
||||||||||||||||||||||||
Производство |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
|
2 |
|
|
0 |
|
||||
a1 = 54 |
|
|
|
|
|
|
20 |
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
p1 = 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
6 |
|
|
|
|
|
2 |
|
|
|
5 |
|
|
0 |
|
||||
a2 = 60 |
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
44 |
|
|
|
|
|
|
|
|
|
|
|
p2 = 2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
7 |
|
|
0 |
|
||||
a3 = 63 |
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
12 |
|
p3 = 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
q1 = 1 |
|
q2 = 4 |
|
|
|
|
q3 = 0 |
q4 = 6 |
|
q5 = –1 |
|
|||||||||||||||
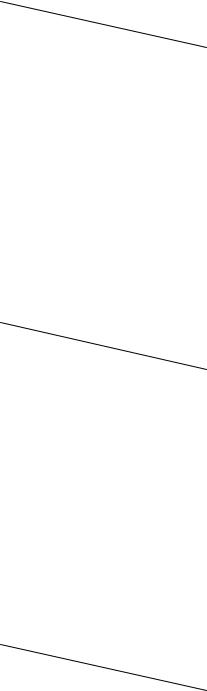
Находим новые потенциалы, новые оценки. Наибольшую положительную оценку будет иметь свободная клетка (1, 4). Для нее строим цикл пересчета
(1, 4) — (1, 1) — (3, 1) — (3, 4),
производим перераспределение (на рис. 4.1.2, б ρmax = 20 ) и получаем тре-
тье базисное допустимое |
|
решение. |
Продолжаем |
процесс |
дальше |
||||||
(табл. 4.1.4—4.1.6). |
В табл. 4.1.6 |
|
11 = 0, |
13 = −3, 15 = −2, |
21 = 0, |
||||||
24 = −1, 33 = −5, |
34 = −4, |
35 = −2 . |
Поскольку |
все |
оценки неположи- |
||||||
тельны, базисное допустимое решение |
|
|
|
|
|
|
|||||
|
|
|
|
0 |
24 |
0 |
30 |
|
|
|
|
|
X = |
|
0 |
4 |
44 0 |
|
|
|
|
||
|
|
|
|
|
|
||||||
|
|
|
|
|
22 |
0 |
0 |
|
|
|
|
|
|
|
41 |
|
|
|
|
||||
является оптимальным.
142
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а |
4.1.4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потребление |
b1 = 41 |
b2 = 50 |
b3 = 44 |
b4 = 30 |
b5 = 12 |
|
|||||||
Производство |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 |
|
3 |
|
|
2 |
|
0 |
|
a1 = 54 |
|
|
34 |
|
|
|
20 |
|
|
|
p1 = 0 |
||
|
|
|
|
|
|
|
|
||||||
|
|
|
– |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
|
6 |
|
2 |
|
|
5 |
|
0 |
|
a2 = 60 |
|
|
|
16 |
|
44 |
|
|
|
|
|
|
p2 = 2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
5 |
|
6 |
|
|
7 |
|
0 |
|
a3 = 63 |
41 |
|
|
* |
|
|
|
|
10 |
|
12 |
|
p3 = 5 |
|
|
|
|
|
|
|
|
||||||
|
|
|
+ |
|
|
|
|
– |
|
|
|
||
|
|
|
|
|
|
|
|||||||
|
q1 = –3 |
q2 = 4 |
q3 = 0 |
q4 = 2 |
q5 = –5 |
|
|||||||
|
|
|
|
|
|
|
|
|
Т а б л и ц а |
4.1.5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потребление |
b1 = 41 |
b2 = 50 |
b3 = 44 |
b4 = 30 |
b5 = 12 |
|
|||||||
Производство |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
4 |
|
3 |
|
2 |
|
|
0 |
|
a1 = 54 |
|
|
24 |
|
|
|
30 |
|
|
|
|
p1 = 0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
|
6 |
|
2 |
|
5 |
|
|
0 |
|
a2 = 60 |
|
|
16 |
|
44 |
|
|
|
* |
|
p2 = 2 |
||
|
|
|
|
|
|
|
|||||||
|
|
|
– |
|
|
|
|
|
+ |
|
|
|
|
|
|
2 |
|
|
5 |
|
6 |
|
7 |
|
|
0 |
|
a3 = 63 |
41 |
|
|
10 |
|
|
|
|
|
|
12 |
|
p3 = 1 |
|
|
|
+ |
|
|
|
|
|
|
– |
|
||
|
q1 = 0 |
q2 = 4 |
q3 = 0 |
q4 = 2 |
q5 = –1 |
|
|||||||
|
|
|
|
|
|
|
|
Т а б л и ц а |
4.1.6 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Потребление |
b1 = 41 |
b2 = 50 |
b3 = 44 |
b4 = 30 |
b5 = 12 |
|
|||||
Производство |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
3 |
|
2 |
|
0 |
|
a1 = 54 |
|
|
24 |
|
|
|
30 |
|
|
|
p1 = 0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
3 |
|
6 |
|
2 |
|
5 |
|
0 |
|
a2 = 60 |
|
|
4 |
|
44 |
|
|
|
12 |
|
p2 = 2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
2 |
|
5 |
|
6 |
|
7 |
|
0 |
|
a3 = 63 |
41 |
|
22 |
|
|
|
|
|
|
|
p3 = 1 |
|
|
|
|
|
|
|
|||||
|
q1 = 1 |
q2 = 4 |
q3 = 0 |
q4 = 2 |
q5 = –2 |
|
|||||
143
Для вычисления потенциалов необходимо m + n – 1 уравнений (4.1.6), т. е. на каждом шаге метода потенциалов число занятых клеток должно сохраняться.
При этом в с л у ч а е н е в ы р о ж д е н н о й з а д а ч и все m + n – 1 компоненты базисного решения будут строго положительными, а всем свободным неизвестным будут соответствовать нулевые перевозки. В с л у ч а е в ы р о ж д е н н о й з а д а ч и некоторые из перевозок, соответствующие базисным неизвестным, также могут быть равны нулю, однако число базисных неизвестных остается равным m + n – 1.
Если на каком-либо шаге перераспределение поставок вдоль цикла пересчета приводит к освобождению более чем одной клетки, все освободившиеся клетки, за исключением одной (не важно, какой), нужно попрежнему считать занятыми. Для того в эти клетки вместо поставки вписывается число нуль, и эти клетки с ф и к т и в н ы м и п о с т а в к а м и участвуют в вычислении потенциалов наравне с другими.
План перевозок, содержащий фиктивные поставки, называется вырожденным. При следующем перераспределении перемещаться будут как раз нулевые, вырожденные поставки, и план перевозок фактически не изменится. Но при этом изменится набор занятых клеток, изменятся потенциалы и оценки свободных клеток, и решение можно будет продолжать.
ПРИМЕР 4.1.2. Требуется решить транспортную задачу со следую-
щими исходными данными: |
|
|
|
|
|
||||
|
|
20 |
|
|
|
|
1 |
2 |
|
a = |
|
40 |
|
, |
b = (20 50), C = |
|
3 |
4 |
|
|
|
|
. |
||||||
|
|
10 |
|
|
|
|
|
3 |
|
|
|
|
|
|
5 |
|
|||
3
РЕШЕНИЕ. Общий объем производства ∑ai = 20 + 40 +10 = 70 совпа-
i =1
4
дает с суммарными запросами потребителей ∑bj = 20 + 50 = 70 , значит,
j =1
транспортная задача является закрытой. Построим в табл. 4.1.7 первое базисное допустимое решение по правилу северо-западного угла.
В задаче m = 3 поставщика, n = 2 потребителя, значит, должно быть заполнено m + n – 1 = 3 + 2 – 1 = 4 клетки транспортной таблицы, но в табл. 4.1.7 заполненными являются только три клетки. В связи с этим невозможно вычислить потенциалы и проверить оптимальность плана перевозок.
Проблема решается просто: достаточно заполнить еще одну клетку фиктивной нулевой поставкой. Например, поставим нуль в клетку (1, 2), теперь у нас заполнены четыре клетки, можно вычислить потенциалы
(табл. 4.1.8).
Вычисленные оценки 21 = 0, 31 = −3 свидетельствуют об оптимальности плана перевозок, содержащегося в табл. 4.1.8.
144

|
|
|
|
|
Т а б л и ц а 4.1.7 |
|
|
|
|
|
|
|
|
Потребление |
b1 = 20 |
b2 = 50 |
|
|
||
Производство |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
a1 = 20 |
20 |
|
|
|
p1 = 0 |
|
|
|
|
|
|||
|
|
|
|
|
||
|
|
3 |
|
4 |
|
|
a2 = 40 |
|
|
40 |
|
p2 = ? |
|
|
|
|
|
|
||
|
|
5 |
|
3 |
|
|
a3 = 10 |
|
|
10 |
|
p3 = ? |
|
|
|
|
|
|||
|
|
|
|
|
||
|
q1 = 1 |
q2 = ? |
|
|
||
|
|
|
|
|
Т а б л и ц а 4.1.8 |
|
|
|
|
|
|
|
|
Потребление |
b1 = 20 |
b2 = 50 |
|
|
||
Производство |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
a1 = 20 |
20 |
|
0 |
|
p1 = 0 |
|
|
|
|
||||
|
|
|
|
|
||
|
|
3 |
|
4 |
|
|
a2 = 40 |
|
|
40 |
|
p2 = 2 |
|
|
|
|
|
|||
|
|
|
|
|
||
|
|
5 |
|
3 |
|
|
a3 = 10 |
|
|
10 |
|
p3 = 1 |
|
|
|
|
|
|
||
|
q1 = 1 |
q2 = 2 |
|
|
||
ПРИМЕР 4.1.3. Требуется решить транспортную задачу со следующими исходными данными:
|
|
25 |
|
|
|
|
5 |
2 |
|
a = |
|
15 |
|
, |
b = (15 40), C = |
|
2 |
4 |
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
3 |
|
|
15 |
|
|
|
5 |
|
|||
3
РЕШЕНИЕ. Общий объем производства ∑ ai = 25 + 15 + 15 = 55 совпада-
i =1
4
ет с суммарными запросами потребителей ∑ bj = 15 + 40 = 55 , значит,
j =1
транспортная задача является закрытой.
Построим в табл. 4.1.9 первое базисное допустимое решение по правилу северо-западного угла.
145

|
|
|
|
|
|
|
|
Т а б л и ц а |
4.1.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Потребление |
b1 = 15 |
b2 = 40 |
|
|
|
||||
|
Производство |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
2 |
|
|
|
|
a1 = 25 |
|
15 |
|
10 |
|
p1 = 0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
a2 = 15 |
|
|
* |
|
15 |
|
p2 = 2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
5 |
|
3 |
|
|
|
|
|
a3 = 15 |
|
|
|
|
15 |
|
p3 = 1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
q1 = 5 |
q2 = 2 |
|
|
|
|||
Вычисляем потенциалы, |
затем оценки свободных клеток |
21 = 5, |
||||||||
31 = 1. Для клетки (2, 1) строим цикл пересчета и перераспределяем поставки. При этом, как видно в табл. 4.1.10, освобождаются две клетки —
(1, 1) и (2, 2).
Чтобы число занятых клеток оставалось равным m + n – 1 = 4, запишем в клетку (1, 1) фиктивную поставку (табл. 4.1.11).
Теперь можно вычислить потенциалы, определить оценки свободных клеток 22 = −5, 31 = 1. Для клетки (3, 1) строим цикл пересчета и пе-
рераспределяем поставки. При этом |
ρmax = 0 , т. е. |
перераспределяется |
|||||||||
фиктивная поставка, она переходит в клетку (3, 1), а клетка |
(1, 1) |
||||||||||
становится свободной. |
|
|
|
|
|
|
|
|
|
||
Оценки свободных клеток 11 = −1, |
22 = −4 |
свидетельствуют об |
|||||||||
оптимальности найденного в табл. 4.1.6 плана перевозок. |
|
||||||||||
|
|
|
|
|
|
|
|
|
Т а б л и ц а |
4.1.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потребление |
|
b1 = 15 |
|
b2 = 40 |
|
|
|
|||
|
Производство |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
2 |
|
|
|
|
a1 = 25 |
|
|
|
|
25 |
|
|
p1 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
a2 = 15 |
|
15 |
|
|
|
|
|
p2 = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
3 |
|
|
|
|
a3 = 15 |
|
|
|
|
15 |
|
|
p3 = ? |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
q1 = ? |
|
q2 = 2 |
|
|
|
|
||
146

|
|
|
|
|
|
Т а б л и ц а 4.1.11 |
|
|
|
|
|
|
|
|
|
Потребление |
b1 = 15 |
b2 = 40 |
|
|
|||
Производство |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
2 |
|
|
a1 = 25 |
|
|
|
|
|
p1 = 0 |
|
|
0 |
|
25 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
a2 = 15 |
|
15 |
|
|
|
p2 = –3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
3 |
|
|
a3 = 15 |
|
* |
|
15 |
|
p3 = 1 |
|
|
|
|
|
|
|||
|
q1 = 5 |
q2 = 2 |
|
|
|||
|
|
|
|
|
Т а б л и ц а 4.1.12 |
|
|
|
|
|
|
|
|
Потребление |
b1 = 15 |
b2 = 40 |
|
|
||
Производство |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
2 |
|
|
a1 = 25 |
|
|
25 |
|
p1 = 0 |
|
|
|
|
|
|||
|
|
|
|
|
||
|
|
2 |
|
4 |
|
|
a2 = 15 |
15 |
|
|
|
p2 = –2 |
|
|
|
|
|
|
||
|
|
5 |
|
3 |
|
|
a3 = 15 |
0 |
|
15 |
|
p3 = 1 |
|
|
|
|
||||
|
|
|
|
|
||
|
q1 = 4 |
q2 = 2 |
|
|
||
Перейдем к обсуждению экономического смысла оценок клеток и потенциалов.
О ц е н к а с в о б о д н о й к л е т к и ij показывает, насколько уменьшатся суммарные расходы по перевозке груза, если поставить единицу груза от i-го производителя j-му потребителю (перераспределив остальные поставки так, чтобы сохранился баланс по строкам и столбцам).
П о т е н ц и а л ы же интерпретируются следующим образом. Производитель с номером i уплачивает перевозчику одну и ту же цену pi за вывоз единицы груза (не важно, какому потребителю этот груз достанется); потребитель с номером j уплачивает перевозчику одну и ту же цену qj за получение единицы груза (не важно, от какого производителя этот груз доставлен); сумма цен, взимаемых при этом с любой пары «производитель
– потребитель», не превосходит реальной стоимости перевозки единицы груза от данного производителя к данному потребителю:
147
pi + q j cij , i = 1, 2,…, m, j = 1, 2,…, n. |
(4.1.12) |
При этом и производители, и потребители не заплатят перевозчику больше, чем реальные транспортные расходы, потому перевозчик может установить цены так, чтобы максимизировать свою прибыль:
m |
n |
|
|
∑ai pi |
+ ∑bj q j |
→ max |
(4.1.13) |
i=1 |
j=1 |
|
|
при условиях (4.1.10).
Переменные pi и qj при этом могут быть как положительными, так и отрицательными: не исключено, что перевозчик платит определенному производителю за право перевозить его продукцию (или потребителю — за право доставлять ему продукцию):
pi , q j .
Задача максимизации функции (4.1.6)—(4.1.7) является двойственной к транспортной задача (4.1.2)—(4.1.5), и приведенная экономическая интерпретации оценок клеток и потенциалов основана на теоремах двойственности.
В реальных условиях pi и qj — это не цены, а надбавки к основному тарифу перевозчика, единому для всех производителей и потребителей.
Усложним транспортную задачу путем учета обязательных и за-
прещенных поставок.
Предположим, что в потребитель iз. поставил условие, чтобы ему не поставляли товар от поставщика jз., а потребитель iоб. потребовал обязательной поставки не менее yiоб. jоб. от поставщика jоб.. Такую задачу можно
решить методом потенциалов с незначительными модификациями. Вопрос с обязательными поставками решается очень легко: нужно
поставку необходимого количества товара предусмотреть прежде всего, а потом решить транспортную задачу с уменьшенными на yiоб. jоб. (если это,
конечно, возможно) параметрами aiоб. и bjоб. .
Что касается запрещенных поставок, то запрет эквивалентен установлению для данного маршрута транспортного тарифа, равного +∞ . На практике соответствующую клетку в транспортной таблице просто зачеркивают и никогда не заполняют, ни при построении первого базисного решения, ни в процессе последующих шагов.
ПРИМЕР 4.1.4. Требуется решить транспортную задачу из примера 4.1.3 при условии, что первому потребителю должно быть поставлено не менее пяти единиц товара от первого поставщика, а поставки от второго поставщика первому потребителю запрещены.
148
Решение. Произведем вначале обязательную поставку 5 единиц товара от первого поставщика первому потребителю. Тогда у первого поставщика останется еще 25 – 5 = 20 нераспределенных единиц товара, а первому потребителю останется поставить 15 – 5 = 10 единиц.
Заполнив транспортную таблицу в табл. 4.1.13, построим в табл. 4.1.13 первое базисное допустимое решение.
|
|
|
Т а б л и ц а |
4.1.13 |
Потребление |
b1 = 10 |
b2 = 40 |
|
|
Производство |
|
|
||
|
|
|
|
|
|
5 |
2 |
|
|
a1 = 20 |
10 |
10 |
p1 = 0 |
|
|
|
4 |
|
|
a2 = 15 |
|
15 |
p2 = 2 |
|
|
5 |
3 |
|
|
a3 = 15 |
* |
15 |
p3 = 1 |
|
|
q1 = 5 |
q2 = 2 |
|
|
Вычисляем потенциалы, находим оценку единственной свободной
клетки 31 = 1, строим цикл пересчета и перераспределяем поставки — |
полу- |
чаем табл. 4.1.14, в которой оценка единственной свободной клетки |
11 = −1, |
значит, план перевозок, содержащийся в табл. 4.1.14, является оптимальным.
|
|
|
Т а б л и ц а |
4.1.14 |
Потребление |
b1 = 10 |
b2 = 40 |
|
|
Производство |
|
|
||
|
|
|
|
|
|
5 |
2 |
|
|
a1 = 20 |
|
20 |
p1 = 0 |
|
|
|
4 |
|
|
a2 = 15 |
|
15 |
p2 = 2 |
|
|
5 |
3 |
|
|
a3 = 15 |
10 |
5 |
p3 = 1 |
|
|
q1 = 4 |
q2 = 2 |
|
|
Вспомним теперь об оптимальной поставке и запишем окончательный оптимальный план перевозок с учетом обязательной и запрещенной поставок:
149
|
|
|
5 |
20 |
|
|
= |
|
0 |
15 |
|
X |
|
. |
|||
|
|
|
|
5 |
|
|
|
10 |
|
||
При этом суммарная стоимость перевозок равна
z = 5 ×5 + 2 × 20 + 2 × 0 + 4 ×15 + 5 ×10 + 3×5 =190 ден. ед.,
это на 65 ден. ед. больше чем в примере 4.1.3.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1.Фирма может выпускать два вида изделий, используя четыре вида оборудования. По нормативам для изготовления одного изделия первого вида оборудование первого, второго, третьего и четвертого вида придется занять соответственно на 2, 3, 4 и 1 день. Аналогично, для изготовления одного изделия второго вида те же станки придется занять в течение 6, 3, 0, 2 дней соответственно. Известен фонд времени оборудования первого вида равен 18 дням, второго вида — 15
дням, третьего и четвертого — соответственно 16 и 8 дням. Удельная прибыль от производства одного изделия первого вида составляет 600 руб., а от производства одного изделия второго вида — 900 руб. Составьте математическую модель поставленной задачи и решите эту задачу: а) графическим методом; б) симплексным методом. Найдите оптимальный план производства, обеспечивающий фирме наибольшую прибыль, а также двойственные оценки каждого вида оборудования и дайте им экономическую интерпретацию.
2.Фирма выпускает из железа и проволоки трансформаторы двух видов. На один трансформатор первого вида тратится 5 кг железа и 3 кг проволоки, изготовление одного трансформатора второго вида требует затрат 3 кг железа и 2 кг проволоки. От реализации одного трансформатора фирма получает прибыль 600 и 500 руб. соответственно. Ежемесячно фирма закупает для 4,8 т железа и 3 т проволоки. Определите: а) сколько трансформаторов каждого вида необходимо выпускать для получения максимальной прибыли; б) каковы двойственные оценки ресурсов; в) по каким максимальным ценам имеет смысл закупать ресурсы; г) каковы остатки ресурсов после выполнения месячного оптимального плана производства; д) какие ресурсы образуют узкие места; е) какое оптимальное количество ресурсов, образующих узкие места, следует заказать дополнительно.
3.Запасы однородного товара на складах заданы вектором a, заявки клиентов на доставку данного товара — вектором b, матрица C содержит транспортные тарифы. Стоимость хранения каждой недо-
150
