
Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие
.pdfДанный результат позволяет ввести новое понятие: рангом матрицы называется максимальное число ее линейно независимых параллельных рядов. Обозначается ранг матрицы A так: rg A. Очевидно, что если
A = m×n , то rg A min{m, n}
Под элементарными преобразованиями матрицы будем понимать преобразования трех типов:
∙перемена местами двух каких-нибудь строк;
∙умножение всех элементов одной из строк матрицы на число, отличное от нуля;
∙прибавление ко всем элементам одной из строк матрицы соответствующих элементов другой строки, умноженных на одно и то же число.
Несложно доказать такую теорему.
ТЕОРЕМА. Элементарные преобразования матрицы не изменяют ее
ранга.
Эта теорема дает способ вычисления ранга матрицы: с помощью элементарных преобразований матрицу приводят (с точностью до перестановки столбцов) к виду
|
1 0 |
0 |
|
|
|||||
|
|
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
||||||
r строк |
|
|
|
|
|
|
|
||
|
|
|
|
||||||
|
|
0 0 |
1 |
|
|
, |
|||
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
0 |
|
|
||||||
где звездочками обозначены произвольные числа, при этом ранг исходной матрицы равен рангу преобразованной матрицы, а ранг преобразованной матрицы, очевидно, равен r.
ПРИМЕР2.2.1. Требуется найти базис и ранг системы векторов — строк матрицы
|
0 |
1 |
2 |
|
A = |
4 |
0 |
1 |
. |
|
|
|
|
|
|
3 |
−1 |
1 |
|
|
|
Решение. Преобразуем матрицу A с помощью элементарных преобразований. Процесс элементарных преобразований иллюстрируется табл. 2.2.1.
51
Т а б л и ц а 2.2.1
|
A |
|
Примечания |
|
|
|
|
0 |
1 |
2 |
II ® I |
4 |
0 |
1 |
I ® II |
3 |
–1 |
1 |
III ® III |
4 |
0 |
1 |
(1/4)×I ® I |
0 |
1 |
2 |
II ® II |
3 |
–1 |
1 |
III ® III |
1 |
0 |
1/4 |
I ® I |
0 |
1 |
2 |
II ® II |
3 |
–1 |
1 |
III – 3×I ® III |
1 |
0 |
1/4 |
I ® I |
0 |
1 |
2 |
II ® II |
0 |
–1 |
1/4 |
III + II ® III |
1 |
0 |
1/4 |
I –(1/9)×III ® I |
0 |
1 |
2 |
II –(8/9)×III ® II |
0 |
0 |
9/4 |
(4/9)×III ® III |
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
|
|
|
|
|
Таким образом, исходная матрица
|
0 |
1 |
2 |
|
A = |
4 |
0 |
1 |
. |
|
|
|
|
|
|
3 |
−1 |
1 |
|
|
|
с помощью элементарных преобразований приведена к виду
|
1 |
0 |
0 |
|
|
|
0 |
1 |
0 |
|
, |
|
|
||||
|
0 |
0 |
1 |
|
|
|
|
|
откуда следует что три строки матрицы A:
(0 1 2), (4 0 1), (3 −1 1) |
(2.2.4) |
представляют собой линейно независимую систему векторов |
|
Эти три вектора (2.2.4) и образуют базис системы векторов — |
строк |
матрицы A. Ранг системы векторов равен числу векторов в базисе этой си- |
|
стемы, т. е., в данном случае, трем. |
|
ПРИМЕР 2.2.2. Нужно определить ранг матрицы А из примера 2.2.1. |
|
Решение. Ранг матрицы равен рангу системы векторов — |
строк |
этой матрицы, т. е., согласно решению примера 2.2.1, rg A = 3 . |
|
Прямая линия с заданным на ней направлением называется осью. Если выбрать на оси некоторую точку O, называемую началом координат, и задать е д и н и ц у и з м е р е н и я (масштаба), то тем самым мы зададим
систему координат на прямой.
52

Две перпендикулярные оси на плоскости с общим началом координат и одинаковой единицей измерения образуют декартову прямоугольную си-
стему координат на плоскости. Одна из осей называется осью абсцисс и
обозначается Oх1, другая — осью ординат (Ox2), а сама система координат обозначается х1Ox2.
Аналогичным образом можно ввести декартову прямоугольную систему координат и в трехмерном пространстве.
Проекции точки на координатные оси называются координатами этой точки. Очевидно, любая точка однозначно задается своими координатами.
С произвольной точкой однозначным образом M связан так называемый радиус-вектор этой точки, т. е. вектор, имеющий те же координаты, что и точка M. С геометрической точки зрения радиус-вектор точки M — это вектор O M , началом которого является начало координат O, а концом
— данная точка M.
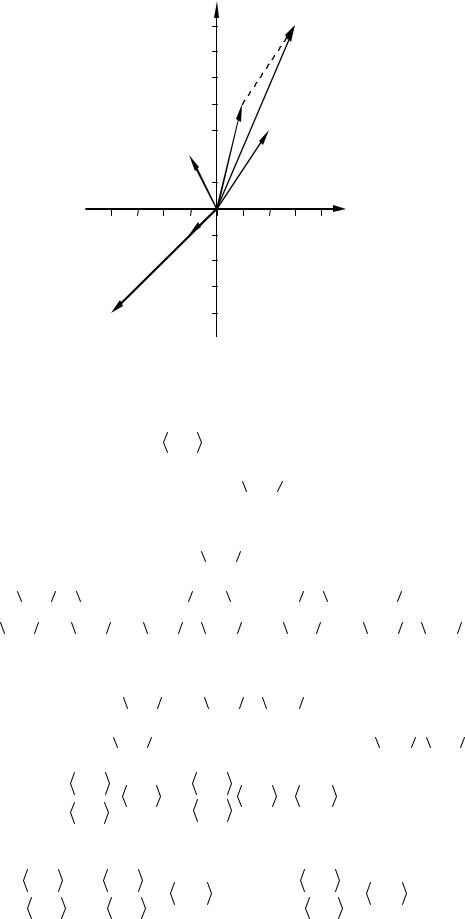
На рис. 2.2.1 изображена декартова прямоугольная система коорди-
нат на |
плоскости. В этой |
системе координат отмечены точки A(1, 4), |
B(2, 3), |
C(–1, 2) и D(1, –1). |
С этими точками связаны их радиус-векторы |
a = (1, 4), b = (2, 3), c = (–1, 2) и d = (–1, –1). |
||
|
Теперь операции над векторами получают наглядную геометриче- |
|
скую интерпретацию.
Для того, чтобы получить сумму векторов a и b, нужно вектор b отложить из конца вектора a и в качестве результата a + b взять вектор с началом в начале вектора a и с концом в конце вектора b.
Чтобы получить вектор λA , нужно построить вектор, который имеет то же направление, что и вектор a, если λ 0 , или противоположное
направление, если λ < 0 , а длину — |
в λ раз больше, чем длина вектора a. |
Построим на рис. 2.2.1, пользуясь этими правилами, векторы a + b и |
|
4d. Их координаты a + b = (3, 7), |
4d = (-4, - 4) совпадают с вычисленными |
по обычным формулам сложения векторов и умножения вектора на число из параграфа 2.1:
a + b = (3, 7) = (1 + 2, 4 + 3), 4d = (-4, - 4) = (-1 × 4, - 1 × 4) .
Аналогии между линейными пространствами произвольной природы и привычными нам прямой линией, плоскостью и обычным трехмерным пространством позволяют пойти дальше: ввести понятия длины вектора, угла между векторами и расстояния между точками в произвольном
линейном пространстве. |
|
|
|
|
|
|
|
|
|
|
Длиной вектора a = (a , a |
, …, a |
n |
) n |
называется число |
||||||
1 2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
| a | = a12 + a22 +…+ an2 = ∑ai2 = a, a , |
||||||||||
|
|
|
|
|
|
i=1 |
|
|
|
|
53
x2
b
a + b
A
 B
B
C
 a
a
c1 |
b |
|
x1 |
||
|
D d O 1
d O 1
4d
Рис. 2.2.1. Декартова прямоугольная система координат на плоскости
НЕРАВЕНСТВО КОШИ — БУНЯКОВСКОГО. Скалярное произведение произвольных векторов a и b не превосходит произведения их длин:
a, b | a | | b | . |
(2.2.5) |
Доказательство. Если a = θ , то  a, b
a, b  = 0, | a | = 0 , откуда и следует
= 0, | a | = 0 , откуда и следует
неравенство (2.2.1), превращающееся в этом случае в равенство. Пусть теперь a ¹ θ и пусть x = aa - b , где a Î — некоторое число. Тогда по свойству скалярного произведения  x, x
x, x  0 [см. формулу (1.1.12)] или
0 [см. формулу (1.1.12)] или
 x, x
x, x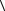 =
= 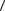 aa - b, aa - b
aa - b, aa - b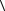 = a
= a  a, aa - b
a, aa - b -
-  b, aa - b
b, aa - b =
=
= a2 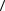 a, a
a, a - a
- a 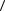 a, b
a, b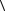 - a
- a 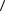 b, a
b, a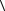 +
+ 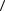 b, b
b, b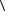 = a2
= a2 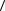 a, a
a, a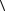 - 2a
- 2a 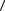 a, b
a, b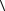 +
+  b, b
b, b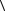 ,
,
т. е. при любом a Î выполняется неравенство
α2 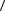 a, a
a, a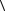 − 2α
− 2α 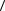 a, b
a, b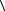 +
+ 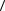 b, b
b, b 0 .
0 .
Так как a ¹ θ , то  a, a
a, a  ¹ 0 и можно положить a =
¹ 0 и можно положить a =  a, b
a, b 

 a, a
a, a  :
:
|
|
|
a, b 2 |
a, a - 2 |
a, b |
|
a, b + b, b 0 , |
||||
|
|
|
|
|
a, a |
||||||
|
|
|
a, a 2 |
|
|
|
|
||||
откуда |
|
|
|
|
|
|
|
|
|
||
|
a, b 2 |
− 2 |
a, b 2 |
+ b, b 0 |
или |
a, b 2 |
b, b . |
||||
|
a, a |
a, a |
a, a |
||||||||
|
|
|
|
|
|
|
|||||
54 |
|
|
|
|
|
|
|
|
|
|
|
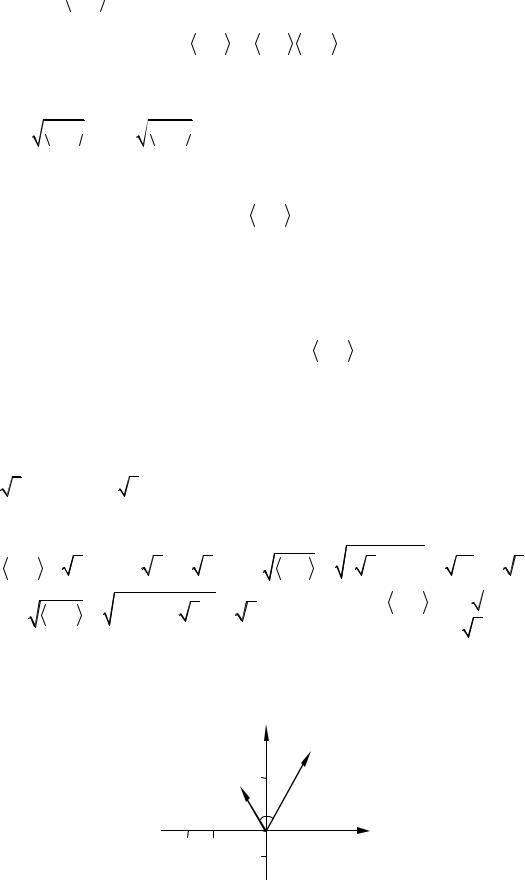
Умножив левую и правую части последнего неравенства на одно и то же число  a, a
a, a  > 0 , получим:
> 0 , получим:
a, b 2 a, a b, b , |
(2.2.6) |
и чтобы теперь получить неравенство (2.2.1), достаточно взять квадратный корень из обеих (неотрицательных) частей неравенства (2.2.2) и вспомнить,
что | a | = 
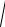
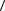 a, a
a, a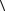 , | b| =
, | b| = 
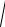
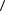 b, b
b, b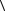 . Справедливость неравенства доказана
. Справедливость неравенства доказана
Поскольку из неравенства Коши — Буняковского следует, что если оба вектора a и b ненулевые, то
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
a, b |
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.2.7) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a | | b | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
между ненулевыми векторами a и b как |
||||||||||||||||||||||||||||||||
можно определить угол ϕ = (a, b) |
|||||||||||||||||||||||||||||||||||||||||||
такое число ϕ = [0, π] , что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
cos j = cos(a, b) |
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
| a | | b | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Читателю рекомендуется убедиться в справедливости неравенства |
||||||||||||||||||||||||||||||||||||||||||
(2.2.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПРИМЕР |
2.2.2. |
|
|
Требуется |
|
|
определить |
угол между |
векторами |
|||||||||||||||||||||||||||||||||
a = ( |
3, 3), b = (-1, |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Решение. Вычисляем последовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= |
|
|
= 2 |
|
|
|
|
|
||||||||||||||||||
a, b = |
|
|
|
|
|
|
|
|
= 2 |
|
|
|
|
|
|
( |
|
)2 + 32 |
|||||||||||||||||||||||||
|
|
|
|
a, a |
|||||||||||||||||||||||||||||||||||||||
3(-1) + 3 |
3 |
3, | a |= |
3 |
12 |
3, |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, b |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
+ ( 3 ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
| b |= b, b |
= |
(-1) |
|
4 = 2, |
cos(a, b) = |
| a | | b | |
= |
|
|
|
|
× |
|
= |
2 |
, |
|||||||||||||||||||||||||||
|
2 3 |
2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
откуда (a, b) = π / 3 = 60 . Рис. 2.2.2 подтверждает это наглядно.
|
|
|
|
x2 |
|
|
|
|
b |
1 |
|
|
a |
||||
π |
|
|
x1 |
|||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O 1 |
|
|
|
|
Рис. 2.2.2. Угол между векторами
55

Два вектора пространства называются ортогональными, если их скалярное произведение равно нулю. С геометрической точки зрения ортогональные векторы перпендикулярны друг другу.
Расстояние между точками A(a , a , …, a ) и B(b , b , …, b ) равно,
1 2 n 1 2 n
очевидно, длине вектора AB = (b1 − a1, b2 − a2 , …, bn − an ) :
|
|
n |
− ai )2 |
|
|
|
|
||
ρ( A, B) = (b1 − a1 )2 + (b2 − a2 )2 +…+ (bn − an )2 = ∑(bi |
= |
|||
|
|
i=1 |
|
|
=
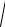
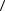 b − a, b −a
b − a, b −a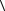 .
.
§2.3. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Вэкономических исследованиях, планировании и управлении приходится рассматривать системы алгебраических уравнений со многими не-
известными величинами. Система из k уравнений первой степени с n неиз-
вестными может быть записана в виде
a11x1 + a12 x2 +…+ a1n xn = b2 , |
|
||||||
a |
x + a |
x +…+ a |
x = b , |
|
|||
|
21 1 |
22 |
2 |
|
2n n |
2 |
(2.3.1) |
|
|
|
|
|
|
||
|
|
|
|||||
a |
x + a |
k 2 |
x +…+ a |
x = b , |
|
||
|
k1 1 |
2 |
|
kn n |
k |
|
|
где н е и з в е с т н ы е x1, x2 ,…, xn |
подлежат определению, а к о э ф ф и - |
||||||
ц и е н т ы a11, a12 ,…, akn |
п р и н е и з в е с т н ы х и с в о б о д н ы е |
||||||
ч л е н ы b1 ,b2 ,…,bk у р а в н е н и й |
заданы, притом первый индекс коэф- |
||||||
фициента совпадает с номером уравнения, в котором содержится данный коэффициент, второй индекс — с номером неизвестной, при которой этот коэффициент поставлен. Кратко запишем систему линейных алгебраических уравнений в следующем виде:
n
∑aij x j = bi , i =1, 2,…, k .
j =1
Совокупность чисел α1, α2 ,…,αn , взятых в определенном порядке,
называют решением системы уравнений (2.3.1), если они, будучи подставлены в уравнения системы на место соответствующих неизвестных, обращают все уравнения в тождества. Решение (α1 , α2 ,…,αn ) системы
(2.3.1) называют неотрицательным, если все его компоненты αi неотри-
цательны.
Система линейных алгебраических уравнений (2.3.1) называется совместной, если она имеет решение. Совместная система называется определенной или неопределенной в зависимости от того, имеет ли она од-
56
но или более решений. Система вида (2.3.1) называется несовместной или противоречивой, если она не имеет решения.
Две системы линейных алгебраических уравнений с одним и тем же числом неизвестных называются эквивалентными, или равносильными, если они или обе несовместны, или обе совместны и имеют одни и те же решения; число уравнений в эквивалентных системах может быть различным. В процессе отыскания решений систему уравнений можно подвергать только таким преобразованиям, которые переводят ее в эквивалентные системы.
Относительно любой системы линейных алгебраических уравнений можно задать вопросы:
∙совместна она или нет;
∙если совместна, то каково число решений;
∙как найти все решения.
Процесс отыскания ответов на первые два вопроса называется ис-
следованием системы, а |
процесс отыскания решений — |
решением системы. |
Мы рассмотрим |
м е т о д Ж о р д а н а — |
Г а у с с а (метод по- |
следовательного исключения неизвестных) для исследования и решения систем линейных алгебраических уравнений, в котором процессы исследования и поиска решений совпадают.
Составим матрицу A из коэффициентов при неизвестных системы линейных алгебраических уравнений. Ее принято называть матрицей системы (2.3.1), а матрицу Aɶ = (A | b) , получающуюся добавлением к A столбца свободных членов системы (2.3.1), называют расширенной матрицей:
|
a11 |
a12 |
a1n |
|
|
a11 |
a12 |
a1n |
b1 |
|
|||||||||||
|
a |
21 |
a |
22 |
|
a |
|
|
|
ɶ |
a |
21 |
a |
22 |
|
a |
2n |
b |
|
||
|
|
|
|
|
|
2n |
|
|
|
|
|
|
2 |
|
|||||||
A = |
|
|
|
|
|
|
; |
A = (A | b) = |
|
|
|
|
|
|
. |
||||||
|
|
|
|
ak 2 |
|
|
|
|
|
|
|
|
|
ak 2 |
akn |
|
|
||||
|
ak1 |
|
akn |
|
|
ak1 |
bk |
||||||||||||||
Очевидно, левые части уравнений системы (2.3.1) совпадают с элементами матрицы-произведения Ax , поэтому систему линейных алгебраических уравнений (2.3.1) можно записать в матричной форме:
Ax = b .
ПРИМЕР 2.3.1. Нужно проверить, является ли вектор
1
y = 2
0
2
решением системы линейных уравнений, которая задана расширенной матрицей
57
|
|
2 |
7 |
3 |
1 |
|
6 |
|
|
|
|||||||
(A | b) = |
|
3 5 |
2 |
2 |
|
4 |
|
|
|
|
. |
||||||
|
|
|
4 |
1 |
7 |
|
2 |
|
|
9 |
|
|
|||||
|
|
|
|
|
|
|||
Решение. Подставим координаты вектора y вместо неизвестных в данную систему линейных уравнений:
2 ×1 + 7 × 2 + 3 × 0 + 1× (-2) = 9 ¹ 6, |
|||
|
×1 + 5 × 2 |
+ 2 × 0 + 2 × (-2) = 9 |
¹ 4, |
3 |
|||
|
×1 + 4 × 2 |
+ 1× 0 + 7 × (-2) = 1 |
¹ 2. |
9 |
|||
Так как вычисленные значения не совпадают с координатами вектора b, то вектор y не является решением данной системы уравнений.
Элементарными преобразованиями системы линейных алгебраиче-
ских уравнений называют преобразования следующих трех типов:
∙перестановка двух каких-нибудь уравнений системы;
∙умножение обеих частей одного из уравнений на любое число, отличное от нуля;
∙прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число.
Нетрудно видеть, что элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему.
Подвергая систему линейных алгебраических уравнений элементарным преобразованиям, можно исключить любую неизвестную из всех уравнений, кроме какого-нибудь одного уравнения. Предположим, что в системе уравнений (2.3.1) коэффициент ars отличен от нуля и что мы ре-
шили исключить неизвестную xs из всех уравнений системы, кроме r-го уравнения. Назовем ars разрешающим коэффициентом, xs — разрешаю-
щей неизвестной, уравнение с номером r — разрешающим уравнением.
Систему уравнений (2.3.1) перепишем в виде
ai1 x1 + … + ais xsar1x1 + … + ars xs
+ … + ain xn |
= bi , |
i ¹ r, |
+ … + arn xn |
= br . |
|
Если умножить r-е уравнение системы на какое-нибудь число l и прибавить к i -му уравнению, то все коэффициенты при неизвестных и свободный член i -го уравнения изменятся и примут значения
a′ |
= a |
ij |
+ λa |
rj |
, j = 1, 2,…, n, |
b′ = b + λb . |
|
ij |
|
|
|
i i |
r |
||
Неизвестная xs исключается из i -го уравнения, если коэффициент при ней станет равным нулю:
a¢ |
= a |
is |
+ la |
rs |
= 0 , |
(2.3.2) |
is |
|
|
|
|
58
для этого необходимо взять
λ = − |
ais |
. |
(2.3.3) |
|
|||
|
ars |
|
|
Исключив таким образом неизвестную xs из всех уравнений систе-
мы (2.3.1), кроме разрешающего уравнения, разделим последнее на разрешающий коэффициент. Система (2.3.1) перейдет в следующую эквивалентную ей новую систему
a¢ x + …+ a¢ |
x |
s−1 |
|
|
+ a¢ |
x |
s+1 |
+…+ a¢ x |
n |
= b¢, i ¹ r, |
||||||
i1 1 |
i,s−1 |
|
|
|
|
i,s+1 |
|
|
in |
i |
||||||
a¢ x + …+ a¢ |
|
x |
s−1 |
+x |
s |
+ a¢ |
|
x |
s+1 |
+…+ a¢ x |
n |
= b¢, |
||||
r1 1 |
r ,s−1 |
|
|
|
r ,s+1 |
|
|
rn |
|
r |
||||||
где неизвестная xs содержится только в r-м уравнении, притом с коэффи-
циентом единица, а остальные коэффициенты при неизвестных и свободные члены связаны с коэффициентами и свободными членами исходной системы (2.3.1), как видно из соотношений (2.3.2) и (2.3.3), формулами:
a¢ |
= a |
- |
ais |
a , |
b¢ = b |
- |
ais |
b , i ¹ r, |
|
|||||
|
|
|
||||||||||||
|
ij |
|
ij |
|
|
|
rj |
i i |
|
|
|
r |
|
|
|
|
|
|
|
|
ars |
|
|
|
|
ars |
(2.3.4) |
||
|
|
|
arj |
|
|
|
|
|
b |
|||||
a¢ |
= |
|
|
|
|
b¢ = |
|
|||||||
|
|
, |
|
|
|
r |
, |
|
||||||
|
|
|
|
|
|
|
||||||||
|
rj |
|
ars |
|
|
|
|
r |
ars |
|
||||
|
|
|
|
|
|
|
|
|
||||||
которые называются формулами исключения.
Формулы исключения удобно применять с помощью правила прямоугольника, суть которого состоит в том, что для получения нового элемента aij′ (или bi¢) надо из преобразуемого элемента aij (или bi ) вычесть
произведение элементов, расположенных в оставшихся противоположных вершинах прямоугольника, деленное на разрешающий элемент (рис. 2.3.1).
○ |
|
|
|
|
|
is |
a |
|
a |
|
|
|
arj |
ij |
|
is |
○○ |
a |
||
|
|
|
|
|||
|
|
|
a′ |
= a |
− |
|
|
|
|
ij |
ij |
|
|
|
|
|
|
|
|
a |
a |
|
a |
|
|
|
□rs |
rj |
|
□rs |
|
|
|
|
a |
|
a |
|
|
|
br |
ij |
|
is |
|
|
|
ais |
○ |
|
|
○○ |
|||
|
|
|
||||
|
|
|
b′ |
= b |
− |
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
a |
a |
|
a |
|
|
|
□rs |
rj |
|
□rs |
|
|
|
|
Рис. 2.3.1. Правило прямоугольника
59
Можно предположить, не теряя общности, что в системе линейных алгебраических уравнений (2.3.1) коэффициент a11 отличен от нуля. Примем
этот коэффициент за разрешающий и исключим по указанным выше правилам неизвестную x1 из всех уравнений системы, кроме первого уравнения.
Система (2.3.1) преобразуется в новую систему линейных алгебраических уравнений, эквивалентную данной, притом число уравнений в новой системе может быть меньше, чем в исходной, так как в процессе преобразований могли появиться уравнения вида
0x1 + 0x2 + +0xn = 0 ,
называемые нуль-уравнениями, которые мы отбрасываем. Далее мы исключим из всех уравнений новой системы, кроме второго, следующую неизвестную, например x2 , если коэффициент при ней в новой системе отли-
чен от нуля, и т. д., если не появилось уравнение вида
0x1 + 0x2 + +0xn = b, b ¹ 0 . |
(2.3.5) |
Процесс последовательного исключения неизвестных закончится либо тогда, когда мы придем к системе, содержащей уравнение вида (2.3.5), что будет означать несовместность исследуемой системы (2.3.1), либо тогда, когда система примет вид
x |
+ g x |
+…+ g x = h , |
|||
|
1 |
1,m+1 m+1 |
1n n |
1 |
|
|
x2 |
+ g2,m+1xm+1 |
+…+ g2n xn |
= h2 |
, |
|
|
|
|
|
(2.3.6) |
|
|
||||
|
|
|
|
|
|
|
|
xm + gm,m+1xm+1 +…+ gmn xn = hm . |
|||
|
|
||||
Система |
уравнений |
(2.3.6) эквивалентна системе |
(2.3.1), притом |
||
m k . Будем говорить, что система линейных алгебраических уравнений
(2.3.1) приведена к предпочитаемому или каноническому виду (2.3.6); неиз-
вестные x1, x2 ,…, xm будем называть базисными, xm+1, xm+2 ,…, xn — свободными. Особенность системы (2.3.6) в том, что в каждом уравнении содержится неизвестная с коэффициентом, равным единице, которая ни в какое другое уравнение не входит, т. е. коэффициенты при базисных неизвестных образуют единичную подматрицу матрицы системы (возможно, после некоторой перестановки уравнений и перенумерации неизвестных). Кратко эту систему записывают в виде
n
xi + ∑ gij x j = hi , i =1, 2,…, m .
j =m+1
Число уравнений в системе (2.3.6) не больше числа неизвестных: m n . При m = n система (2.3.6) имеет вид
60
