Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новокузнецкий институт (филиал КемГУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие

.pdf

Скачиваний:

1245

Добавлен:

19.04.2015

Размер:

6.01 Mб

Скачать

☆

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 3722 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

инвестиций между предприятиями, которое максимизирует суммарный прирост мощности или прибыли

z = z1 (u1 )+ z2 (u2 )+…+ zn (un )→max

при ограничении по общей сумме инвестиций

u1 + u2 +…+ un = b .

Будем считать, что все управления ui принимают только целые неотрицательные значения

ui {0,1, 2, 3,…}.

Функции zi (ui ) мы считаем заданными, заметив, что их определе-

ние — довольно трудоемкая экономическая задача.

Воспользуемся для решения этой задачи методом динамического программирования.

Введем параметр состояния и определим функцию состояния. За параметр состояния x примем денежную сумму, выделяемую нескольким предприятиям, а ф у н к ц и ю с о с т о я н и я Fk (x) определим как максимальную прибыль на первых k предприятиях, если они вместе получают x ден. ед. Параметр x может изменяться от 0 до b.

Если из x руб. k-е предприятие получит xk		руб., то каково бы ни было
это значение, остальные x − uk руб. естественно распределить между пред-
приятиями от первого до ( k −1)-го так, чтобы была получена максимальная
прибыль Fk −1	(x −uk ).	равна zk (uk )+ Fk −1 (x −uk ).
Тогда	прибыль k предприятий будет

Нужно выбрать такое значение uk между 0 и x, чтобы эта сумма была максимальной. Таким образом, мы приходим к р е к у р р е н т н о м у с о - о т н о ш е н и ю

Fk (x) = max {zk (uk )+ Fk −1 (x −uk )}

0 uk x

для k = 2, 3, …, n. Если же k = 1, то

F1 (x) = z1 (x) .

ПРИМЕР 7.1.1. Производственное объединение состоит из четырех предприятий (n = 4). Общая сумма капитальных вложений равна 700 млн. руб. (b = 700), выделяемые предприятиям суммы кратны 100 млн. руб. Если i-

е предприятие получит инвестиции в объеме	x млн. руб., то прирост годовой
прибыли на этом предприятии составит zi (x)	млн. руб. в год (значения функ-

ций zi (x) приведены в табл. 7.1.1). Требуется найти такое распределение

211

u1 u = u2un

инвестиций между предприятиями, которое максимизирует суммарный прирост прибыли на всех предприятиях.

													Т а б л и ц а			7.1.1
		x		0	100	200	300	400	500		600	700
		z1(x)		0	20	34	46	53	55		60	60
		z2(x)		0	18	29	45	62	78		90	98
		z3(x)		0	25	41	52	74	82		88	90
		z4(x) 0			30	52	76	90	104		116	125
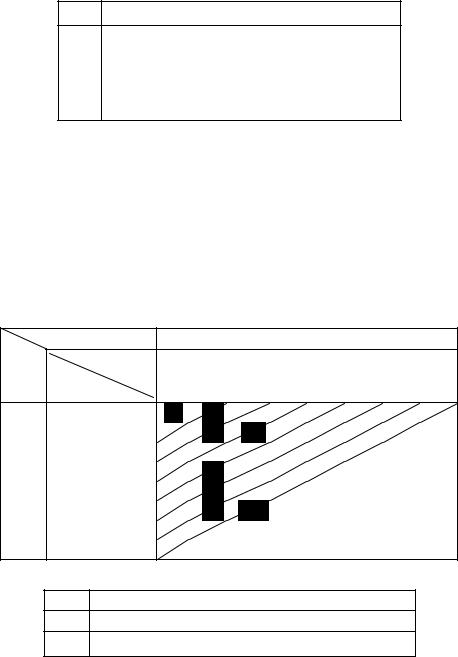
РЕШЕНИЕ.		Прежде			всего		заполняем			табл. 7.1.2.				Для	каждого
x = 0, 100, 200, …, 700 рассматриваем все возможные значения управления
u2 = 0, 100, 200, …,			x, и значения F1 ( x − u2 ) = z1							( x − u2 ) складываем со зна-
чениями z2 (u2 ) . На каждой							северо-восточной диагонали находим
наибольшее число (выделяя его цветом) и указываем соответствующее
значение u (x) .
2
Затем заполняем табл. 7.1.3.
													Т а б л и ц а			7.1.2
			x – u2			0	100	200	300		400	500	600 700
u2				F1(x −u2)		0	20	34	46		53	55	60	60
u2	z2	(u2)				0	20	34	46		53	55	60	60
	z2	(u2)
0				0		0	20	34	46		53	55	60	60
100				18		18	38	52	64		71	73	78
200				29		29	49	63	75		82	84
300				45		45	65	79	91		98
400				62		62	82	96	108
500				78		78	98	112
600				90		90	110
700				98		98
													Т а б л и ц а			7.1.3

x	0	100	200	300	400	500	600	700
F2(x)	0	20	38	52	65	82	98	112
u (x)	0	0	100	100	300	400	500	500
2

Продолжая процесс, табулируем функции F3 ( x), u3 (x) и т. д. (табл. 7.1.4—7.1.5).

В табл. 7.1.6 заполняем только одну диагональ для значения x = 700. Наибольшее число на этой диагонали

212

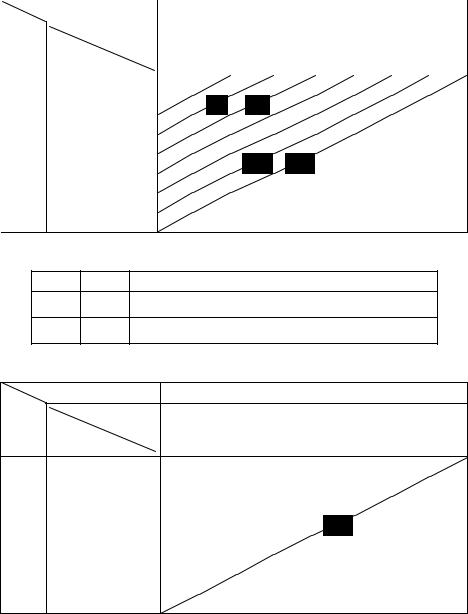
z = 155 млн. руб.,

причем четвертому предприятию должно быть выделено

u4 = u4 (700) = 300 млн. руб.

Т а б л и ц а 7.1.4

		x – u3	0	100		200		300	400	500	600	700
x3		F2(x −u3)	0	20		38		52	65	82	98	112
x3	z3	(u3)	0	20		38		52	65	82	98	112
	z3	(u3)

0		0	0	20		38		52	65	82	98	112
100		25	25	45		63		77	90	107	123
200		41	41	61			79	93	106	123
300		52	52	72		94		112	126

400		74	74		94	112		126
500		82	82	102		120
600		88	88	106
700		90	90

Т а б л и ц а 7.1.5

x	0	100	200	300	400	500	600	700
F3(x)	0	25	45	63	79	94	112	126
u (x)	0	100	100	100	200	400	400	400
3

									Т а б л и ц а		7.1.6
		x – u4	0	100	200	300	400	500	600	700
u4		F3(x −u4)	0	25	45	63	79	94	112	126
u4	z4	(u4 )	0	25	45	63	79	94	112	126
	z4	(u4 )
0		0								126
100		30							142
200		52						146
300		76					155
400		90				153
500		104			149
600		116		141
700		125	125
На долю остальных трех предприятий остается 400 млн. руб. Из
табл. 7.1.5 видно, что третьему предприятию должно быть выделено

u3 = u3 (700 − u4 ) = u3 (400) = 200 млн. руб.

Продолжая обратный процесс, находим

u2 = u2 (700 − u4 − u3 ) = u2 (200) = 100 млн. руб.

На долю первого предприятия остается

u1 = 700 − u4 − u3 − u2 = 100 млн. руб.

213

Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:

u1 =100, u2 =100, u3 = 200, u4 = 300 .

Оно обеспечивает производственному объединению наибольший возможный прирост прибыли 155 млн. руб.

Читателю рекомендуется проверить выполнение равенства z1 (u1 )+ z2 (u2 )+ z3 (u3 )+ z4 (u4 )= z .

§ 7.2. МНОГОШАГОВАЯ ЗАДАЧА УПРАВЛЕНИЯПРОИЗВОДСТВОМИ ЗАПАСАМИ

Рассмотрим предприятие, которое производит партиями некоторые изделия. Предположим, что предприятие получило заказы на n месяцев, причем размеры заказов значительно меняются от месяца к месяцу, поэтому иногда целесообразнее выполнить одной партией заказы нескольких месяцев (и затем хранить изделия, пока они не потребуются), чем выполнять заказ именно в тот месяц, когда он должен быть отправлен. Необходимо составить план производства на указанные n месяцев с учетом затрат

на производство и хранение изделий. Введем обозначения:
u j	— число изделий, производимых в j-й месяц;
x j	— величина запаса к началу j-го месяца (это число не содер-
	жит изделий, произведенных в j-м месяце);
d j	— число изделий, которые должны быть отгружены в j-м месяце;
f j	(xj+1, u j ) — затраты на хранение и производство изделий в j-м месяце.
	Будем считать, что величины запасов к началу первого месяца x1 и
к концу последнего xn+1 заданы.
	Задача состоит в том, чтобы найти план производства
	u1

	u = u2	,	(7.2.1)


	un

компоненты которого удовлетворяют условиям материального баланса

x j + u j	− d j = x j+1,	j =1, 2, …, n		(7.2.2)
и минимизируют суммарные затраты за весь планируемый период
	n
z = ∑ f j (xj+1, u j )→ min ,				(7.2.3)
	j=1
причем
x j {0,1, 2, 3, …},	u j {0, 1, 2, 3, …},		j =1, 2, …, n .	(7.2.4)

214

Прежде чем приступить к решению поставленной задачи, заметим, что для любого месяца j величина x j+1 запаса к концу месяца должна удо-

влетворять ограничениям
0 x j+1 d j+1 + d j+2 +…+ dn ,	(7.2.5)

т. е. объем производимой продукции u j на этапе j может быть настолько велик, что запас x j+1 удовлетворяет спрос на всех последующих этапах, но не имеет смысла иметь x j+1 больше суммарного спроса на всех последую-

щих этапах. Кроме того, из соотношений (7.2.2) и (7.2.4) непосредственно следует, что управление u j должно удовлетворять ограничениям

0 u j d j + x j+1 .	(7.2.6)
Следует также заметить, что переменные x j , u j	могут принимать

только целые неотрицательные значения.

Будем решать задачу (7.2.1)—(7.2.6) методом динамического программирования.

Введем параметр состояния и составим функцию состояния.

За параметр состояния x примем наличный запас в конце k-го месяца

x= xk +1 ,

афункцию состояния Fk ( x) определим как минимальные затраты за первые k месяцев при выполнении условия (7.2.5):

		k		j (				j )
F (x) =	min	∑	f		x	j+1	, u		,
k	u , u , ..., u	∑				j+1
	1 2	k j=1

где минимум берется по неотрицательным целым значениям u1 , u2 , …, uk , удовлетворяющим условиям

x j + u j − d j = x j+1,	j =1, 2, …, k −1,
xk + uk − dk	= x .	(7.2.7)

Учитывая, что

min ∑

u1 , u2 , …, uk j=1

j (

j )

k −1

j (

j+1

, u

= min

k +1

, u

min

∑

j+1

, u

u , u

, …, u

j )

1 2

k −1 j=1

и величина запаса xk к концу (k – 1)- го периода, как видно из уравнения

(7.2.7), равна

xk = x + dk −uk ,

приходим к рекуррентному соотношению

Fk (x) = min {fk (x, uk )+ Fk −1 (x + dk −uk )},

215

где минимум берется по единственной переменной uk , которая, согласно (7.2.6), может изменяться в пределах

0 uk dk + x ,

принимая целые значения, причем верхняя граница зависит от значений

параметра состояния, изменяющегося в пределах
0 x d k +1 + d k +1 +…+ d n ,	(7.2.8)
а индекс k может принимать значения
k = 2, 3, 4, …, n.
Если k = 1, то
F1 (x2 ) = min f1 (x2 , u1 ),
u1
где
u1 = x + d1 − x1 ,
0 x d 2 + d3 +…+ d n ,
т. е. на начальном этапе при фиксированном уровне	x1 исходного запаса

каждому значению параметра x отвечает только одно значение переменной u1 , что несколько уменьшает объем вычислений.

Применив вычислительную процедуру динамического программирования, на последнем шаге (при k = n) находим значение последней компоненты un оптимального решения, а остальные компоненты определяем как

	n
uk = uk xn+1 +	∑	(d j	−u*j	) , k =1, 2, …, n −1.
	j=k +1

Рассмотрим более подробно функции f j (xj+1, u j ) и рекуррентные соотношения. Пусть

ϕj (u j )= au2j +bu j + c ,

ϕj (u j )— затраты на производство (закупку) u j единиц продукции на этапе j;

h j	— затраты на хранение единицы запаса, переходящей из этапа j в
	этап j + 1.

Тогда затраты на производство и хранение на этапе j равны

f (x + , u )= ϕ (u )+ h x + = au2 +bu +c + h x + .

j j 1 j j j j j 1 j j j j 1

216

Выведенные ранее рекуррентные соотношения динамического программирования для решения задачи управления производством и запасами в нашем случае принимают вид

F (x + )= min{au2 +bu + c + h x + + F − (x )},

k k 1 k k k k 1 k 1 k uk

где

k = 2, 3, 4, …, n,

0 xk +1 dk +1 + dk +2 +…+ dn , 0 uk dk + xk +1 ,

xk = xk +1 + dk − uk .

Если же k = 1, то

(7.2.9)

(7.2.10)

F1 (x2 )= min{au12 +bu1 + c + h1x2},	(7.2.11)
x1
0 x2 d2 + d3 +…+ dn ,	(7.2.12)
0 u1 d1 + x2 ,	(7.2.13)
x1 + u1 − d1 = x2 .
Остается заметить, что полезно обозначить выражение в фигурных
скобках в (7.2.9) через
Wk (xk +1, uk )= auk2 +buk + c + hk xk +1 + Fk −1 (xk )
и записать рекуррентное соотношение (7.2.9) в виде
Fk (x = xk +1 )= min Wk (xk +1, uk ),	(7.2.14)
uk

где минимум берется по целочисленной переменной uk , удовлетворяющей условию (7.2.10).

ПРИМЕР 7.2.1. Рассматривается трехэтапная система управления запасами с дискретной продукцией и динамическим детерминированным спросом. Заявки потребителей на продукцию составляют: на первый этап d1 = 3 единицы, на второй — d2 = 2 , на третий — d3 = 4 единицы. К началу первого этапа на складе имеется 2 единицы продукции, т. е. начальный уровень запаса равен y1 = 2 . Затраты на хранение единицы продукции на разных этапах различны и составляют соответственно h1 =1, h2 = 3, h3 = 2 ден. ед. Затраты на производство uj единиц продукции на j-м этапе определяются функцией

ϕj (u j )= u2j +5u j + 2,

j =1, 2, 3,

т. е. a = 1, b = 5, c = 2. Требуется указать, сколько единиц продукции на отдельных этапах следует производить, чтобы заявки потребителей были

217

удовлетворены, а суммарные затраты на производство и хранение за все три этапа были наименьшими.

			РЕШЕНИЕ. Воспользовавшись рекуррентными соотношениями, после-
довательно				вычисляем				F1 ( x2 ), F2 (x3 ), F3 ( x4 )	и соответственно находим
u	( x	2	) , u (x ) , u		( x	4	) .
1		2	2	3	3	4
			Положим k = 1. Согласно (7.2.11) имеем
							F1	(x2 ) = min{u12 + 5u1 + 2 + x2}.
								u1
			Учтем, что согласно (7.2.12) параметр состояния x = x2 может при-
нимать целые значения на отрезке
								0 x2 d2 + d3 ,
								0 x2 2 + 4,
т. е.
								x2 = 0, 1, 2, 3, 4, 5,	6 .

При этом, вообще говоря, каждому значению параметра состояния должна отвечать определенная область изменения управления u1 , характеризуемая условием (7.2.13)

0 u1 3 + x2 .

Однако объем производства на первом этапе u1 не может быть меньше единицы, так как спрос d1 = 3 , а исходный запас x1 = 2 . Кроме того, из балансового уравнения

x1 + u1 − d1 = x2

непосредственно следует, что объем производства связан со значением параметра состояния x = x2 соотношением

u1 = x2 + d1 − x1 = x2 + 3 − 2 = x2 +1 .

(7.2.15)

В этом и состоит особенность первого этапа. Если задан уровень запаса к началу первого этапа, то каждому значению x2 отвечает единственное значение u1 , и потому

F1 (x2 )=W1 (x2 , u1 ).

Придавая x2 различные целые значения от 0 до 6 и учитывая

(7.2.15), находим:

x2 = 0, u1 = 0 +1 =1, W1(1, 0) =12 + 5 ×1+ 2 +1×0 = 8, x2 =1, u1 =1+1 = 2, W1 (2, 1) = 22 + 5 × 2 + 2 +1×1 =17,

и т.д. Значения функции состояния F1 (x2 ) представлены в табл. 7.2.1.

218

Т а б л и ц а 7.2.1

x = x2	0	1	2	3	4	5	6
F1 (x2 )	8	17	28	41	56	73	92

u1 (x2 )	1	2	3	4	5	6	7

Переходим ко второму этапу. Полагаем k = 2 и табулируем функцию F2 ( x3 ) с помощью соотношения (7.2.14):

F2 (x3 ) = minW2	( x3 , u2 ) = min{au22 + bu2 + c + h2 x3 + F1 ( x2 )} =	(7.2.16)
u2	u2
	= min{u22 + 5u2 + 2 + 3x3 + F1 ( x2 )}.
	u2
Здесь минимум берется по единственной переменной u2 , которая
может изменяться, согласно (7.2.10), в пределах
0 u2 d 2 + x3 или 0 u2 2 + x3		(7.2.17)

где верхняя граница зависит от параметра состояния x = x3 , который, согласно (7.2.8), принимает значения на отрезке

0 y3 d3 , т. е. 0 y3 4 ,

а аргумент x2 в последнем слагаемом справа в соотношении (7.2.16) связан с x3 и u2 балансовым уравнением

x2 + u2 − d 2 = x3 ,

откуда следует, что

					x2 = x3 + d 2 − u2			= x3 + 2 − u2 .	(7.2.18)
		Придавая параметру состояния x = x различные значения от 0 до 4,
будем последовательно вычислять W								( x, u3 ), а затем определять	F ( x) и
u (x) . Положим, например, x = x							2	2	2
u (x) . Положим, например, x = x						3	= 2 . Тогда, согласно (7.2.17),
2						3
					0 u2 4 ,
т. е. управление u2					может принимать значения 0, 1, 2, 3, 4, и каждому значе-
нию u2		отвечает определенное значение x2 , вычисляемое по формуле (7.2.18):
						x2 = 4 − u2 .
		Последовательно вычисляем:
если u	2	= 0 , то x	2	= 4 − 0 = 4 , W (2, 0) = 02 + 5 ×0 + 2 + 3× 2 + F (4) =8 + 56 =64 ,
	2		2		2			1

219

u	2	= 1 ,	x	2	= 4 − 1 = 3 ,	W (2, 1) =12	+ 5 ×1+ 2 + 3 × 2 + F (3) =14 + 41=55 ,
	2			2		2		1
u	2	= 2 ,	x	2	= 4 − 2 = 2	, W (2, 2) = 22		+ 5 × 2 + 2 + 3× 2 + F (2) =22 + 28=50 ,
	2			2		2		1

u	2	= 3 ,	x	2	= 4 − 3 = 1 ,	W (2, 3) = 32	+ 5×3 + 2 + 3×2 + F (1) =32 +17 = 49 ,
	2	= 4 ,		2	= 4 − 4 = 0	2	1
u	2	= 4 ,	x	2	= 4 − 4 = 0	, W (2, 4) = 42	+ 5 × 4 + 2 + 3 × 2 + F (0) =44 + 8=52 .
	2			2		2	1
		Наименьшее из полученных значений W2 — это F2 (2) , т. е.
		F2 ( x3	= 2) = min W2 (2, u2 ) = min{64, 55, 50, 49, 52} = 49 ,
					u2

причем минимум достигается при значении u2 , равном u2 ( x3 = 2) = 3 .

Аналогично для значения параметра x = x3 = 3 , проведя необходимые вычисления, найдем

F	( x = 3) = 63,	u ( x = 3) = 3 .
2	3	2	3

Процесс табулирования функции F2 ( x3 ) приведен в табл. 7.2.2, а

результаты табулирования сведены в табл. 7.2.3.

Переходим к следующему этапу. Полагаем k = 3 и табулируем функцию F3 ( x4 ) :

F3 (x = y4 ) = min{ax32 + bx3 + c + h3 y4 + F2 ( y3 )}.

Вычисляем значение функции состояния только для одного значения аргумента x = x4 = 0 , так как не хотим оставлять продукцию в запас в конце исследуемого периода. Процесс вычислений приведен в табл. 7.2.4. Получаем

F3 ( x4 = 0) = min W3 (0, u3 ) = min{80, 71, 65, 62, 62} = 62 ,

причем минимум достигается при двух значениях переменной u 3 , равных

u	(x = 0) = 3 или	u	(x = 0) = 4 .
3	4	3	4

Таким образом, мы получили не только минимальные общие затраты на производство и хранение продукции, но и оптимальное управление на последнем шаге: u3 Î{3, 4}.

Рассмотрим случай, когда на последнем этапе планируется выпус-

кать три единицы продукции:

u3 = 3 .

Остальные компоненты оптимального решения найдем по обычным правилам метода динамического программирования.

Чтобы найти предпоследнюю компоненту, учтем, что

x3 + u3 − d3 = x4 или 3 + x3 − 4 = 0 ,

откуда

x3 = 1.

220

<<< < Предыдущая 10 11 12 13 14 15 16 17 18 19 20 2122 / 3722 23 24 25 26 27 28 29 30 31 32 33 34 > Следующая >>>

Соседние файлы в папке Семестровая 1 (Методы оптимальных решений)

#
19.04.201553.55 Кб144(Методы оптимальных решений) Семестровая 1.docx
#
19.04.20156.01 Mб1245Методы оптимальных решений учебное пособие.pdf
#
19.04.2015177.31 Кб404Пример решения задачи симплекс методом..docx
#
19.04.201562.74 Кб72Пример решения ЗЛП графическим методом и анализ чувствительности модели.docx