f (X )
+ he(0)
e(jk+)e(jk−)
e(jk+)e(jk−) = 0, j = 1, 2,…, n, |
(5.3.6) |
e(jk+) 0, e(jk−) 0, j = 1, 2,…, n. |
(5.3.7) |
Эту задачу после введения фиктивных переменных (для преобразования к предпочитаемому виду) можно решить симплексным методом. При этом для учета условий = 0 при вычислительной реализации сим-
плексного метода необходимо следить за тем, чтобы не вводить в базис одновременно переменные e(1)j+ и e(1)j − с одинаковым индексом j (j = 1, 2, .., n).
ПРИМЕР 5.3.1. Требуется найти приближение к оптимальному решению задачи выпуклого программирования (3.2.7)—(3.2.9) из примера 3.2.1, для чего провести три первые итерации метода возможных направлений, выбрав в качестве начального приближения вектор
(0) = 1
X .8
Решение. Как было показано в примере 2.2.1, начальное приближение
x(0) 1
= 8
является в н у т р е н н е й точкой множества допустимых решений. Очередное приближение x(1) к оптимальному решению задачи выбе-
рем в направлении наискорейшего возрастания целевой функции:
|
(0) |
= grad f (x |
(0) |
|
−2(x1 |
− 8) |
|
|
|
|
|
−2(1 − 8) |
|
14 |
|
|
|
|
e |
|
|
) = |
−2(x |
− 8) |
|
|
|
( 0 ) |
= |
−2(8 − 8) |
|
= |
0 |
. |
|
|
|
|
|
2 |
|
|
|
x=x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем границы шага смещения h в направлении e(0), при котором
точка |
|
|
|
1 + 14h |
1 |
14 |
x(1) = x(0) + he(0) = |
|
+ h |
|
= |
|
|
8 |
|
0 |
|
8 |
будет оставаться во множестве допустимых решений. Запишем условия допустимости:
|
|
3(1 + 14h) + 8 15, |
|
+ 14h + 8 10, |
1 |
1 + 14h 0, |
|
|
|
0. |
8 |
Решениями этой системы неравенств являются все h [−1 / 14;1 / 14] . Выберем h из этого отрезка таким образом, чтобы значение целевой функции в точке x(1) = x(0) было максимальным.
Для этого найдем точку максимума функции
Φ0 (h) = f (x( 0 ) + he( 0 ) ) = −(1 +14h − 8)2 − (8 − 8)2 = −(14h − 7)2 = −49(2h −1)2
одной переменной h на отрезке h Î-[1 / 14;1 / 14].
Производная F¢0 (h) = -49 × 2(2h -1) = -98(2h -1) обращается в нуль в точке h =1/ 2 , положительна при h <1 / 2 и отрицательна при h >1/ 2 , поэтому точка h =1/ 2 является точкой глобального максимума функции F0 (h) , а максимум функции F0 (h) на отрезке h Î-[1 / 14;1 / 14] достигается в точке h(0) =1 / 14 .
Таким образом, если выбрать шаг смещения h(0) =1 / 14 в направлении
|
14 |
|
|
|
e(0) = |
|
|
|
|
|
0 |
|
|
|
|
наискорейшего роста целевой функции f (x) , то при движении от точки |
x(0) |
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
к точке |
|
|
|
|
|
|
x(1) = x(0) + h(0)e(0) |
= |
1 |
+14h(0) |
|
2 |
|
|
|
= |
|
|
|
|
8 |
|
|
8 |
целевая функция возрастет наибольшим образом, а точка X(1) останется во |
множестве допустимых решений. |
|
|
|
|
|
|
Итак, получили новое приближение |
|
|
|
x(1) |
2 |
|
|
|
|
= |
|
|
|
|
|
8 |
|
|
|
|
к оптимальному решению задачи (3.2.7)—(3.2.9).
Переходим ко в т о р о м у ш а г у метода возможных направлений. Точка x(1) является г р а н и ч н о й точкой множества допустимых решений; второе из ограничений (3.2.8) выполняется в этой точке как равенство, а первое ограничение (3.2.8) и оба ограничения (3.2.9) — как
строгие неравенства:
3 × 2 + 8 < 15,
+ =
2 8 10,
2 > 0,
8 > 0.
Поэтому если двигаться в направлении
|
−2(x |
−8) |
|
|
|
|
|
grad f (x(1) ) = |
1 |
|
|
|
|
|
−2(x2 |
− 8) |
|
|
x=x(1) |
|
|
|
|
−2(2 − 8) |
12 |
|
= |
|
= |
0 |
|
|
−2(8 −8) |
|
|
наискорейшего возрастания целевой функции, то новое приближение может выйти за границы области допустимых решений, т. е. направление
grad f (x(1) ) = |
12 |
|
|
|
|
|
|
0 |
|
не является возможным в точке |
|
|
|
|
|
2 |
|
|
|
x(1) = |
8 |
. |
|
|
|
|
|
Возможное направление
возрастания целевой функции f (X ) |
в точке x(1) выберем так, чтобы оно яв- |
лялось оптимальным решением задачи (5.3.2)—(5.3.3), |
которая в данном |
случае имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z =12e(1) |
+ 0e(1) |
|
→ max, |
(5.3.8) |
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e(1) |
+ e(1) |
0, |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
(5.3.9) |
|
|
|
|
|
|
|
|
e1(1) |
|
+ |
|
e2(1) |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы свести эту задачу к задаче линейного программирования, |
представим переменные e(1) |
и e(1) |
|
как разности новых неотрицательных |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
переменных e(1) 0, |
e(1) 0, |
e(1) 0, |
|
e(1) 0 : |
|
|
|
|
|
1+ |
1− |
|
|
2+ |
|
|
|
2− |
|
|
|
|
|
|
|
|
|
e(1) |
|
= e(1) |
− e(1) , |
|
|
|
e(1) |
|
|
= e(1) |
− e(1) , |
|
|
1 |
1+ |
|
|
1− |
|
|
|
|
|
2 |
2+ |
2− |
|
причем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e(1)e(1) = 0, e(1)e |
(1) = 0 . |
|
|
|
|
1+ |
1− |
|
2+ |
2− |
|
|
При этом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e(1) |
|
= e(1) |
+ e(1) |
, |
|
|
|
e(1) |
|
|
= e(1) |
+ e(1) , |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1+ |
|
|
1− |
|
|
|
|
|
2 |
|
|
2+ |
2− |
|
и задача (5.3.8)—(5.3.9) примет вид
z =12e1(1)+ −12e1(1)− → max,
e(1) |
− e(1) |
+ e(1) |
− e(1) |
|
0, |
|
+ |
|
− |
2 |
+ |
2 |
− |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
e(1) |
+ e(1) |
+ e(1) |
+ e(1) |
1, |
|
|
1+ |
|
1− |
2+ |
2− |
|
|
|
|
|
e(1)e(1) |
= 0, |
e(1)e(1) |
= 0, |
|
|
|
1+ |
1− |
|
|
2+ |
|
2− |
|
|
e(1) 0, |
e(1) |
0, |
e(1) 0, e(1) |
0. |
1+ |
|
|
1− |
|
|
2+ |
|
2− |
|
Будем решать эту задачу симплексным методом, введя предварительно дополнительные переменные s1 и s2, чтобы преобразовать неравенства в равенства:
z =12e(1) −12e(1) |
→ max, |
|
(5.3.10) |
|
|
1+ |
1− |
|
|
|
|
e(1) |
− e(1) |
+ e(1) |
− e(1) |
+ s |
|
= 0, |
|
1+ |
1− |
2+ |
2− |
1 |
|
|
|
e1(1) |
+ e1(1) |
+ e2(1) |
+ e2(1) |
+ s2 |
=1, |
(5.3.11) |
+ |
− |
+ |
− |
|
|
= 0, |
e1(1)+ e1(1)− |
|
|
|
|
|
e(1)e(1) |
|
|
|
|
= 0, |
|
2+ |
2− |
|
|
|
|
|
|
e(1) 0, e(1) 0, e(1) 0, e(1) |
0. |
(5.3.12) |
1+ |
|
1− |
2+ |
2− |
|
|
|
Для учета условий e1(1)+ e1(1)− = 0, e2(1)+ e2(1)− = 0 при вычислительной реализации симплексного метода будем следить за тем, чтобы не вводить в базис одновременно переменные e(1)j+ и e(1)j − (j = 1, 2).
Симплексная таблица представлена в табл. 5.3.1.
|
|
|
|
|
|
|
|
Т а б л и ц а 5.3.1 |
cɶ |
Базис |
h |
12 |
–12 |
0 |
0 |
0 |
0 |
|
e(1) |
e(1) |
e(1) |
e(1) |
s1 |
s2 |
|
|
|
|
1+ |
1− |
2+ |
2− |
|
|
|
0 |
s1 |
0 |
1 |
–1 |
1 |
–1 |
1 |
0 |
|
0 |
s2 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
z0 − z |
0 – z |
–12 |
12 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
12 |
e1(1)+ |
0 |
1 |
–1 |
1 |
–1 |
1 |
0 |
|
0 |
s2 |
1 |
0 |
2 |
0 |
2 |
–1 |
1 |
|
|
z0 − z |
0 – z |
0 |
0 |
12 |
–12 |
12 |
0 |
|
|
|
|
|
|
|
|
|
|
|
12 |
e1(1)+ |
1/2 |
1 |
0 |
1 |
0 |
1/2 |
1/2 |
|
0 |
e2(1)− |
1/2 |
0 |
1 |
0 |
1 |
–1/2 |
1/2 |
|
|
z0 − z |
6 – z |
0 |
24 |
12 |
0 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
В результате мы получили оптимальное решение
e(1) |
= 1 / 2, |
e(1) |
= 0, |
e(1) |
= 0, |
e(1) |
= 1 / 2 . |
1+ |
|
1− |
|
2+ |
|
2− |
|
задачи (5.3.10)—(5.3.12).
Теперь легко найти оптимальное решение задачи (5.3.8)—(5.3.9):
e(1) |
= e(1) |
− e(1) |
= 1 / 2, |
e(1) |
= e(1) |
− e(1) |
= −1 / 2 . |
1 |
1+ |
1− |
|
2 |
2+ |
2− |
|
Тем самым, мы определили н а п р а в л е н и е очередного шага:
Найдем г р а н и ц ы шага смещения h в направлении e(1), при кото-
ром точка |
|
|
|
|
|
2 |
1 / 2 |
2 + h / 2 |
x(2) = x(1) + he(1) = |
|
+ h |
|
= |
|
8 |
|
|
−1 / 2 |
8 |
− h / 2 |
будет оставаться во множестве допустимых решений. Имеем:
3(2 + h / 2) + 8 − h / 2 15,
|
+ h / 2 + 8 − h / 2 10, |
2 |
|
+ h / 2 0, |
2 |
|
− h / 2 0. |
8 |
Точка x( 2) остается во множестве допустимых решений при всех h [−4;1]. Выберем h из этого отрезка таким образом, чтобы значение це-
левой функции f (x) в точке x( 2) было максимальным. Для этого найдем точку максимума функции
Φ1 (h) = f (x(1) + he(1) ) = −(2 + h / 2 − 8)2 − (8 − h / 2 − 8)2 |
= |
= −(h / 2 − 6)2 − h2 / 4 = −h2 / 2 + 6h − 36 |
|
одной переменной h на отрезке h −[4;1] . |
|
′ |
h = 6 , поло- |
Производная Φ1(h) = −h + 6 обращается в нуль в точке |
жительна при h < 6 и отрицательна при h > 6 , поэтому точка h = 6 является точкой глобального максимума функции Φ1 (h) , а максимум функции
Φ1 (h) на отрезке h [−4;1] достигается в точке h(1) = 1.
165
Таким образом, если выбрать шаг смещения h(1) =1 в направлении
наискорейшего роста целевой функции f (x) , то при движении от точки
x(1) 2
= 8
к точке
|
2 + h(1) |
/ 2 |
|
|
5 / 2 |
|
x(2) = x(1) + h(1)e(1) = |
8 − h |
(1) |
|
|
= |
|
|
|
|
/ 2 |
15 / 2 |
|
целевая функция возрастет наибольшим образом, а точка x( 2) останется во множестве допустимых решений.
Итак, получили очередное приближение
к оптимальному решению задачи (3.2.7)—(3.2.9).
Начинаем т р е т и й ш а г метода возможных направлений.
Точка x( 2) является граничной точкой множества допустимых решений; оба ограничения (3.2.8) выполняются в этой точке как равенства, а оба ограничения (3.2.9) — как строгие неравенства:
3 × 5 / 2 +15 / 2 =15,
|
+15 / 2 =10, |
5 / 2 |
|
> 0, |
5 / 2 |
Поэтому если двигаться в направлении
|
-2(x |
- 8) |
|
|
-2(5 / 2 - 8) |
11 |
|
|
|
|
|
grad f (x( 2) ) = |
1 |
- 8) |
|
|
|
= |
|
= |
|
|
-2(x2 |
|
|
x=x( 2 ) |
|
-2(15 / 2 - 8) |
|
1 |
|
|
|
наискорейшего возрастания целевой функции, то новое приближение может выйти за границы области допустимых решений, т. е. направление
не является возможным в точке
Составим задачу линейного программирования для определения возможного направления e(2) :
z = 11e( 2) |
− 11e( 2) |
+ e( 2) |
− e( 2) |
→ max, |
|
1+ |
|
1− |
|
2+ |
2− |
|
|
3e(2) |
− 3e(2) |
+ e(2) |
− e(2) |
0, |
|
|
1+ |
|
1− |
|
2+ |
2− |
|
|
|
|
− e1(2)− |
+ e2(2)+ |
− e2(2)− |
|
|
e1(+2) |
|
0, |
|
e(2) |
|
+ e(2) |
+ e(2) |
+ e(2) |
1, |
|
|
1+ |
|
1− |
|
2+ |
2− |
|
|
|
e( 2)e( 2) = 0, e( 2)e( 2) = 0, |
|
|
1+ |
|
1− |
|
2+ |
2− |
|
|
e( 2) 0, e( 2) 0, e( 2) |
0, e( 2) |
0. |
1+ |
|
|
1− |
|
2+ |
|
2− |
|
Оптимальное решение этой задачи равно
e1(+2) = 1 / 4, e1(−2) = 0, e2( 2)+ = 0, e2( 2)− = 3 / 4
(симплексная таблица представлена в табл. 5.3.2), откуда находим направление очередного шага
Найдем границы шага смещения h в направлении e(2), при котором
точка |
|
|
|
|
|
|
|
5 / 2 |
1 / 4 |
|
5 / 2 + h / 4 |
|
x(3) = x(2) + he(2) = |
|
+ h |
−3 |
|
= |
|
|
15 / 2 |
|
|
/ 4 |
15 / 2 − 3h / 4 |
|
будет оставаться во множестве допустимых решений. Имеем:
3(5 / 2 + h / 4) + 15 / 2 − 3h / 4 15,
+ + −
5 / 2 h / 4 15 / 2 3h / 4 10,
5 / 2 + h / 4 0,
15 / 2 − 3h / 4 0.
Этой системе неравенств удовлетворяют все h [0; 5]. Выберем h из этого отрезка таким образом, чтобы значение целевой функции f (x) в
точке x(3) = x(2) + he(2) было максимальным.
Для этого найдем точку максимума функции
Φ2 (h) = f (x( 2) |
+ he( 2) ) = −(5 / 2 + h / 4 − 8)2 − (15 / 2 − 3h / 4 − 8)2 = |
|
|
= −(h / 4 − 11 / 2)2 − (3h / 4 + 1 / 2)2 |
|
одной переменной h на отрезке h [0;10]. |
|
Производная |
Φ′ (h) = (8 − 5h) / 4 обращается в нуль в точке h = 8 / 5 |
, |
|
2 |
|
положительна при |
h < 8 / 5 и отрицательна при h > 8 / 5 , поэтому точка |
h = 8 / 5 является точкой глобального максимума функции Φ2 (h) и точкой локального максимума этой функции на отрезке h [0;10] .
Получаем очередное приближение: |
|
|
|
|
5 / 2 + 2 / 5 |
|
29 / 10 |
|
|
2,9 |
|
x(3) = |
|
= |
|
= |
6,3 |
. |
15 / 2 − 6 / 5 |
|
63 / 10 |
|
|
|
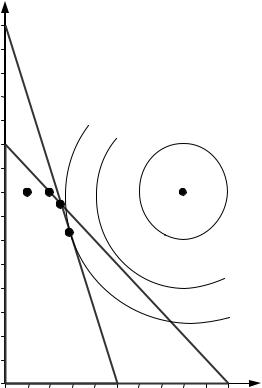
Итерационный процесс метода возможных направлений иллюстрируется рис. 5.3.1.
Заметим, что x(3) — это точное решение задачи (3.2.7)—(3.2.9) ; оно было получено в примере 2.2.1.
Т а б л и ц а 5.3.2
cɶ |
Базис |
h |
11 |
–11 |
1 |
–1 |
0 |
0 |
0 |
e1(1)+ |
e1(1)− |
e2(1)+ |
e2(1)− |
s1 |
s2 |
s3 |
0 |
s1 |
0 |
3 |
–3 |
1 |
–1 |
1 |
0 |
0 |
0 |
s2 |
0 |
1 |
–1 |
1 |
–1 |
0 |
1 |
0 |
0 |
s3 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
z0 − z |
0 – z |
–11 |
11 |
–1 |
1 |
0 |
0 |
0 |
0 |
s1 |
0 |
0 |
0 |
–2 |
2 |
1 |
–3 |
0 |
11 |
e1(1)+ |
0 |
1 |
–1 |
1 |
–1 |
0 |
1 |
0 |
0 |
s3 |
1 |
0 |
2 |
0 |
2 |
0 |
–1 |
1 |
|
z0 − z |
0 – z |
0 |
0 |
10 |
–10 |
0 |
11 |
0 |
–1 |
e2(1)− |
0 |
0 |
0 |
–1 |
1 |
1/2 |
–3/2 |
0 |
11 |
e1(1)+ |
0 |
1 |
–1 |
0 |
0 |
1/2 |
–1/2 |
0 |
0 |
s3 |
1 |
0 |
2 |
2 |
0 |
–1 |
2 |
1 |
|
z0 − z |
0 – z |
0 |
0 |
0 |
0 |
5 |
–4 |
0 |
–1 |
e2(1)− |
3/4 |
0 |
3/2 |
1/2 |
1 |
–1/4 |
0 |
3/4 |
11 |
e1(1)+ |
1/4 |
1 |
–1/2 |
1/2 |
0 |
1/4 |
0 |
1/4 |
0 |
s2 |
1/2 |
0 |
1 |
1 |
0 |
–1/2 |
1 |
1/2 |
|
z0 − z |
2 – z |
0 |
4 |
4 |
0 |
3 |
0 |
2 |
x2
|
15 |
|
|
14 |
|
|
13 |
|
|
12 |
|
|
11 |
|
|
10 |
|
|
9 |
|
|
8 |
x(0) |
|
x(1) x(2) |
|
|
|
7 |
x(3) |
|
6 |
|
|
|
5 |
|
|
4 |
|
|
3 |
|
|
2 |
|
|
1 |
x1 |
|
|
0
1 2 3 4 5 6 7 8 9 10
Рис. 5.3.1. Итерационный процесс метода возможных направлений
§ 5.4. МЕТОД УСЛОВНОГО ГРАДИЕНТА
Опишем теперь метод условного градиента. Пусть x( k ) — очередное приближение к оптимальному решению задачи выпуклого программирова-
ния (3.1.1)—(3.1.2) — |
такая точка x( k ) множества допустимых решений, что |
|
grad f (x(k ) ) ¹ θ . |
|
Тогда в окрестности точки x( k ) целевая функция f (x) |
может быть |
представлена в виде |
|
|
|
|
|
|
|
|
|
|
f (x) = f (x( k ) ) + (grad f (x( k ) ), x - x( k ) ) + o ( |
|
|
|
x - x( k ) |
|
|
|
) . |
|
|
|
|
|
|
Будем максимизировать на допустимом множестве линейную |
функцию |
f ( k ) (x) = (grad f (x( k ) ), x - x( k ) ) , |
|
|
(5.4.1) |
которая является приближением разности f (x) - f (x( k ) ) с точностью до величины o (
 x - x( k )
x - x( k ) 
 ) .
) .
Пусть xɶ( k ) — решение вспомогательной задачи максимизации функции (5.4.1) при ограничениях (3.1.2).
169
|
Следующее приближение x( k +1) к оптимальному решению исходной |
задачи (3.1.1)— (3.1.2) |
построим по формуле |
|
|
|
|
x( k +1) = x( k ) + h( k ) (xɶ( k ) − x(k ) ), |
(5.4.2) |
в которой величину шага смещения h(k ) выберем как |
|
|
|
|
h(k ) = min{1; hɶ( k ) }, |
|
ɶ |
(k ) |
выбирается из условия наибольшего роста целевой функции f (x) |
где h |
|
при перемещении из точки x( k ) в точку |
|
|
|
|
x( k ) + hɶ(k ) (xɶ( k ) − x( k ) ). |
|
|
Тогда, поскольку множество допустимых решений |
выпукло, а |
h( k ) [0;1] , точка x( k +1) |
(5.4.2) останется допустимым решением. |
|
Отметим, что вспомогательная задача максимизации функции (5.4.1) при ограничениях (3.1.2) является также задачей выпуклого программирования. Процесс ее решение оказывается, однако, достаточно простым в случае, когда ограничения (3.1.2) являются линейными.
ПРИМЕР 5.4.3. Требуется найти приближение к оптимальному решению задачи выпуклого программирования (3.2.7)—(3.2.9) из примера 3.2.1, для чего провести три первые итерации метода условного градиента, выбрав в качестве начального приближения вектор
x(0) 1 .
= 8
Решение. Как было показано в примере 2.2.1, начальное приближение
x(0) 1
= 8
является допустимым решением. При этом
|
−2(x − 8) |
|
|
|
|
|
grad f (x(0) ) = |
1 |
|
|
|
|
−2(x2 −8) |
|
|
x=x( 0 ) |
|
|
|
−2(1 −8) |
14 |
|
= |
|
= |
0 |
. |
|
−2(8 −8) |
|
|
Поставим вспомогательную задачу максимизации функции (5.4.1) при ограничениях (3.1.2):
f (0) (x) = (grad f (x(0) ), x − x(0) )=14(x1 −1) + 0(x2 −8) =14x1 −14 → max ,
3x1 + x2 15,
x1 + x2 10,
x1 0, x2 0 .


 x - x( k )
x - x( k ) 
 ) .
) .