
Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие
.pdf
Т а б л и ц а 7.2.2
|
n |
|
x =xk+1 |
0 uk dk +xk+1 |
|
|
xk = xk+1+dk−uk |
Wk (xk+1 , uk )=φk (uk )+hk xk+1 +Fk−1 (xk ) |
||||||||||||||||||||||||||||
0 xk+1 ∑ dj |
uk |
|||||||||||||||||||||||||||||||||||
|
j=k+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
0 x |
d |
3 |
x =x |
3 |
0 u d |
+x |
3 |
x |
2 |
x |
= x |
+d |
−u |
W (x |
, u |
2 |
)=au2 |
+bu |
+c +h x |
+F |
(x |
2 |
) |
|||||||||||||
3 |
|
|
|
|
2 |
2 |
|
|
|
2 |
|
|
3 |
2 |
2 |
2 |
3 |
|
|
|
|
2 |
2 |
2 |
|
3 |
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 x |
4 |
ξ=y |
3 |
0 u 2 +x |
3 |
u |
|
x |
= x |
+2−u |
W |
(x |
, u |
)=u2 |
+5u |
+2 +3x |
3 |
+F (x |
) |
|
||||||||||||||||
3 |
|
|
|
|
|
|
2 |
|
2 |
2 |
|
3 |
|
2 |
2 |
|
3 |
|
|
|
2 |
2 |
2 |
|
|
1 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u2 =0 |
x2 =2−0 =2 |
W (0,0) =02 +5 0 +2+3 0 +F (2)=2+28 =30 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
=0 |
0 u 2 |
|
|
u =1 |
x =2−1=1 |
W (0,1) =12 |
+5 1+2+3 0 +F (1)=8 +17 =25 |
||||||||||||||||||||||||
|
|
|
3 |
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
u2 =2 |
x2 =2−2=0 |
|
|
2 |
+5 2+2+3 0 +F1(0)=16 +8 = 24 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W2(0,2) =2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u =0 |
x =3−0 =3 |
W2(1, 0)=02 +5 0 +2+3 1+F1(3)=5+41=46 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u =1 |
x =3−1=2 |
W (1,1)=12 |
+5 1+2+3 1+F (2)=11+28 =39 |
|||||||||||||||||||||
|
|
|
x3 =1 |
0 u2 3 |
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
u2 =2 |
x2 =3−2 =1 |
W (1,2)=22 |
|
+5 2+2+3 1+F (1)=19 +17 = 36 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u2 =3 |
x2 =3−3=0 |
W (1, 3)=32 +5 3+2+3 1+F (0)=29 +8 =37 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
3 |
=2 |
|
… |
|
|
|
… |
|
|
|
… |
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u2 =0 |
x2 =5−0 =5 |
W2 (3, 0) =02 +5 0 +2 +3 3 +F1 (5) =11 +73 =84 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u =1 |
x =5−1=4 |
W (3,1) =12 +5 1 +2 +3 3 +F (4) =17 +56 =73 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x3 =3 |
|
|
|
|
|
u =2 |
x =5−2=3 |
W (3, 2) =22 |
|
+5 2 +2 +3 3 +F (3) =25 +41 =66 |
|||||||||||||||||||||||
|
|
|
0 u2 5 |
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
u2 =3 |
x2 =5−3=2 |
W (3,3) =32 +5 3 +2 +3 3 +F (2) =35 +28 = 63 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u2 =4 |
x2 =5−4 =1 |
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
W (3, 4) =42 |
+5 4 +2 +3 3 +F (1) =47 +17 =64 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u2 =5 |
x2 =5−5=0 |
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
W (3, 5) =52 +5 5 +2 +3 3 +F (0) =61 +8 =69 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u =0 |
x |
2 |
=6−0 =6 |
W (4, 0) =02 |
|
+5 0 +2 +3 4 +F (6) =14 +92 =106 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
u =1 |
x |
2 |
=6−1=5 |
W (4, 1) =12 |
|
+5 1 +2 +3 4 +F (5) =20 +73 =93 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
u =2 |
x |
2 |
=6−2 =4 |
W (4, 2) =22 |
+5 2 +2 +3 4 +F (4) =28 +56 =84 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
x |
|
=4 |
0 u 6 |
|
|
u =3 |
x |
2 |
=6−3=3 |
W (4, 3) =32 |
|
+5 3 +2 +3 4 +F (3) =38 +41 =79 |
|||||||||||||||||||||
|
|
|
3 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
u2 =4 |
x2 =6−4 =2 |
W2 (4, 4) =42 +5 4 +2 +3 4 +F1 (2) =50 +28 = 78 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u2 =5 |
x2 =6−5=1 |
W2 (4, 5) =52 +5 5 +2 +3 4 +F1 (1) =64 +17 =81 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u2 =6 |
x2 =6−6 =0 |
W2 (4, 6) =62 +5 6 +2 +3 4 +F1 (0) =80 +8 =88 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
221


Рассмотрим ценообразование акций в рамках биномиальной мо-
дели Кокса — Росса — Рубинштейна.
Предположим для простоты, что на рынке обращается о д н а акция, и ее стоимость в конце периода времени t составляет St.
Предположим также, что инвестор имеет возможность:
∙размещать средства на банковском счете и брать с него в долг;
∙покупать и продавать акции.
Тогда для этого инвестора на рынке существует б е з р и с к о в ы й
а к т и в (банковский счет) B и |
р и с к о в ы й а к т и в (акция) S. |
Будем считать, что на банковский счет начисляются проценты с |
|
э ф ф е к т и в н о й с т а в к о й |
i: год делится на n периодов, проценты за |
часть года вычисляются как простые, а накапливаются как сложные, так что за время T > 0 сумма на счете увеличивается в (1 + i/n)[nT] раз (квадратными скобками обозначена целая часть числа): Bt = B0(1 + i/n)[nT].
Будем предполагать, что о п е р а ц и о н н ы е и з д е р ж к и, связанные с переводом средств между активами, отсутствуют, а также что активы являются б е з г р а н и ч н о д е л и м ы м и, т. е. можно купить и продать любую часть акции, положить на счет и снять с него любую его часть.
Предположим вначале, что в течение года проценты начисляются один раз, а стоимость акции может увеличиться в u раз или увеличиться в d раз (уменьшиться в 1/d раз), причем d < 1 < 1 + i < u (рис. 7.3.1).
|
|
|
|
St |
|
S0u |
|
|
|
||
|
|
||||
S0 |
|
||||
S0d |
|
|
|
|
t |
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
1 |
Рис. 7.3.1. Изменение цены акции за один год |
|||||
Н а и д е а л ь н о м р ы н к е о т с у т с т в у ю т а р б и т р а ж - |
|||||
н ы е в о з м о ж н о с т и, т. е. |
невозможно извлечь безрисковый доход, |
||||
больший чем процент, начисляемый на банковский счет.
Предположение о том, что на рынке отсутствуют арбитражные возможности, означает, что математическое ожидание цены акции на таком рынке к концу года MS1 должно совпадать с суммой, которая оказалась бы на банковском счете к концу года, если бы сумма S0 была в начале года положена на банковский счет, т. е. с суммой S0(1 + i):
MS1 = S0(1 + i).
Истинные вероятности того, что в течение данного периода акция подорожает или подешевеет, нам неизвестны, но в предположении отсут-
224
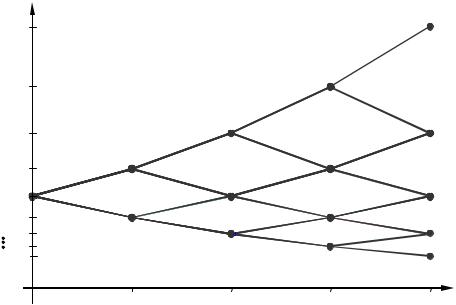
S0u4 St
S0u3
S0u2
S0u
S0
S0d
S0d4
t
0 |
1/4 |
1/2 |
3/4 |
1 |
Рис. 7.3.2. Изменение цены акции в течение четырех периодов
ПРИМЕР 7.3.1. Требуется составить ряд распределения цены акции к концу года, разбив этот год на четыре периода, если текущая цена акции составляет S0 = 35 руб., годовая безрисковая процентная ставка составляет i = 9,6% и известно, что в каждом периоде акция может возрасти в цене или упасть в цене в u = 1,105 раз.
Решение. Вероятность, нейтральная к риску,
p = |
1+ i / 4 − d |
= |
1,024 − 0,905 |
|
≈ 0,595, |
1 – p |
|
≈ 0,405 |
|
u − d |
1,105 − 0,905 |
(4) |
|||||||
(4) |
|
|
|
|
|||||
|
|
|
|
|
|
||||
(здесь d = 1 / u = 1 / 1,105 ≈ 0,905 ).
Теперь мы можем составить ряд распределения цены акции к концу четвертого периода: цена принимает значения
S0ukd 4 – k
соответственно с вероятностями
P4 (k) = C4k p(k4) (1− p(4) )4−k , k = 0, 1, 2, 3, 4.
Окончательно имеем:
S1 |
23, 48 |
28,66 |
35,00 |
42,74 |
52,18 |
. |
p |
0,027 |
0,158 |
0,348 |
0,341 |
0,125 |
|
|
|
|
|
|
|
|
Банковский счет, акции и облигации называются основными финансовыми инструментами. На их базе могут быть построены более сложные финансовые инструменты — п р о и з в о д н ы е.
226
|
|
|
|
[nT ] |
|
|
|
M |
|
∑max{S0uk d[nT ]−k − X ; 0}C[knT ] p(kn) (1− p(n) )[nT ]−k |
|
|
|
|
k =0 |
|
|
T = |
|
|
= |
|
. (7.3.4) |
|
+ i / n)[nT ] |
(1+ i / n)[nT ] |
|||
(1 |
|
|
|||
ПРИМЕР 7.3.2. Требуется определить рациональную стоимость европейского опциона покупателя с терминальной стоимостью X = 40 руб. и сроком исполнения 1 год, выписанного на акцию из условия примера 7.3.1.
Решение. Ряд распределения дохода от исполнения опциона при расчетах по четырехпериодной биномиальной модели имеет следующий вид:
C1 |
0,00 |
2,74 |
12,18 |
. |
p |
0,027 + 0,158 + 0,348 = 0,533 |
0,341 |
0,125 |
Ожидаемый доход от исполнения опциона покупателя, равный математическому ожиданию случайной величины C1, составляет
4
M = ∑max{S0uk d 4−k − X ; 0}Ck4 p(k4) (1− p(4) )4−k =
k=0
=0 ×0,027 + 0 ×0,158 + 0 × 0,348 + 2,737 ×0,341 +12,182 × 0,126 = 2, 456.
Окончательно получаем, что
|
= |
|
M |
= |
2, 456 |
≈ 2, 23 |
руб., |
|
T |
|
|
|
|
||||
|
+ i / 4)4 |
1,0244 |
||||||
|
(1 |
|
|
|
||||
т. е рациональная стоимость такого опциона равна 2 руб. 23 коп. (что существенно меньше текущей цены акции и цены исполнения опциона!).
На реальном рынке продавцу опциона выгодны цены, не меньшие рациональной стоимости опциона, а покупателю — не бó льшие.
Успех зависит от скорости и качества получения информации и принятия решения. Предположим, что инвестор А получил ту же информацию и провел те же расчеты, что в примерах 7.3.1—7.3.2, и в результате нашел рациональную стоимость опциона, равную 2 руб. 23 коп. Предположим, что другой инвестор Б получил информацию по своим каналам и провел расчеты с другой степенью точности, получив в результате свое значение рациональной стоимости данного опциона — например, 7 руб. 15 коп. Если они договорятся, что Б купит у А 10 000 таких опционов, скажем, по 4 руб., то в момент подписания сделки оба будут чрезвычайно довольны собой (А считает, что продал опционы дороже, чем они стоит на самом деле, а Б думает, что ему удалось купить опционы дешевле их рациональной цены). Но на самом деле выиграет из них кто-то один — это станет ясно в момент исполнения! Такова типичная иллюстрация деятельности на финансовых рынках, где финансовые потоки текут от тех, кто не успевает быстро принимать правильные решения, к тем, кто успевает это делать. И если несколько сотен (и даже десятков) лет назад определяющую роль играла скорость получения информации, то прогресс в области ин-
228

ПРИМЕР 7.3.3. Требуется найти рациональную стоимость европейского опциона продавца с терминальной стоимостью X = 40 руб. и сроком исполнения 1 год, выписанного на акцию из условия примера 7.3.1.
Решение. По теореме о паритете опционов покупателя и продавца
PT − CT + S0 = |
|
X |
|
, |
|
|
(1+ i / n)[nT ] |
||||
откуда |
|
|
|
|
|
P1 = 2,23 − 35 + |
40 |
|
≈ 3,61, |
||
|
|
|
|||
1,0244 |
|
||||
т. е. рациональная стоимость такого опциона равна 3 руб. 61 коп.
Можно рациональную стоимость европейского опциона продавца найти и другим способом — по ряду распределения дохода от его исполнения
P |
16,52 |
11,34 |
5,00 |
0,00 |
|
1 |
|
|
|
|
. |
p |
0,027 |
0,158 |
0,348 |
0, 467 |
|
|
|
|
|
|
|
Находим математическое ожидание дохода от исполнения опциона:
M P1 = 16, 52 × 0, 027 + 11, 33 × 0,158 + 5, 00 × 0, 348 + 0 × 0, 467 = 3, 98.
и дисконтируем его на срок его действия:
|
MP |
3,969 |
|
|
P1 = |
1 |
= |
|
≈ 3,61 руб. |
(1+ i / 4)4 |
1,0244 |
|||
Перейдем к рассмотрению ценообразования американских опционов. Оказывается, американский опцион покупателя может быть выгодно исполнять т о л ь к о в п о с л е д н и й м о м е н т с р о к а е г о д е й - с т в и я. Это влечет справедливость следующей теоремы.
ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ ЕВРОПЕЙСКИХ И АМЕРИКАНСКИХ ОПЦИОНОВ ПОКУ-
ПАТЕЛЯ. Рациональная стоимость американского опциона покупателя совпадает с рациональной стоимостью аналогичного европейского опциона покупателя.
Однако американский о п ц и о н |
п р о д а в ц а часто бывает в ы - |
г о д н о и с п о л н и т ь д о с р о ч н о, |
поэтому его рациональная стои- |
мость может оказаться такой же, как у соответствующего европейского опциона (если досрочное исполнение окажется невыгодным) или выше (если будет выгоднее исполнить опцион досрочно).
Это приводит к тому, что теорема о паритете для американских опционов превращается в неравенство
P(амер.) − C(амер.) + S |
X |
. |
||
T |
T |
0 |
(1+ i / n)[nT ] |
|
Для оценки рациональной стоимости американских опционов про-
давца обычно пользуются методом динамического программирования.
В самом деле, в биномиальной модели процесс изменения цены акции распадается на n периодов (э т а п о в), поэтому процесс планирования
230
