Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие

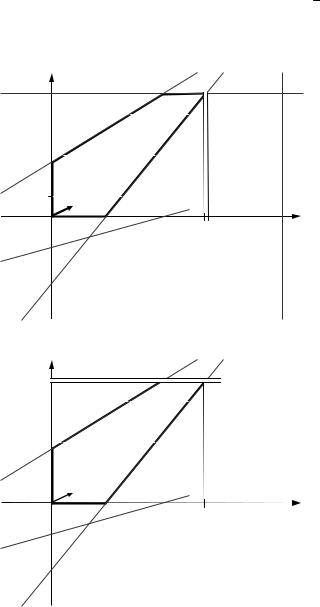
Это ветвление иллюстрируется рис. 4.2.2, а. Задача (4.2.5) имеет нецелочисленное оптимальное решение t1 = 46, t3 = 181 / 3 = 60 13 , а задача (4.2.6)

не имеет решений (значит, эта ветвь метода ветвей и границ обрывается).

б) второй шаг ветвления

Рис. 4.2.2. Применение метода ветвей и границ к решению целочисленной задачи о расшивке узких мест производства

131

Произведем ветвление в задаче (4.2.5); оно проиллюстрировано рис. 4.2.2, б; получим две новые задачи:

t3 = 60 , а задача (4.2.10) не имеет решений (значит, эта ветвь обрывается). Таким образом, получено оптимальное целочисленное решение задачи о расшивке узких мест производства: необходимо дополнительно по-

лучить 46 единиц первого ресурса и 60 единиц третьего.

Отметим, что в данной задаче целочисленного программирования решение получено достаточно быстро и является тривиальным (округлением компонент оптимального решения сопутствующей нецелочисленной задачи). В задачах целочисленного программирования, вообще говоря, так бывает довольно редко.

§ 4.1. ТРАНСПОРТНАЯ ЗАДАЧА

Транспортная задача формулируется следующим образом. Однородный продукт, сосредоточенный в m пунктах производства (хранения) в количествах a1, a2 ,…, am единиц, необходимо распределить между n пунк-

тами потребления, которым необходимо соответственно b1, b2 ,…, bn единиц. Стоимость перевозки единицы продукта из i-го пункта отправления в j-й пункт назначения — транспортный тариф — равна cij и известна для всех маршрутов. Необходимо составить план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и суммарные транспортные расходы по доставке продуктов были минимальны.

Если производство и потребление сбалансированы, т. е. суммарные запасы продукта у поставщиков равны суммарным запросам потребителей:

132

то такая транспортная задача называется закрытой или замкнутой.

Если же суммарные запасы продукта у поставщиков строго больше или строго меньше, чем суммарные запросы потребителей, то такая задача называется открытой.

Для сведения открытой задачи к закрытой вводятся фиктивные пункты производства или потребления. Если суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, вводится ф и к т и в н ы й п о т р е б и т е л ь, запросы которого равны

если же суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, то вводится ф и к т и в н ы й п о - с т а в щ и к, запас продукта у которого равен

Если в результате решения транспортной задачи окажется, что определенное количество продукта придется доставить фиктивному потребителю, на практике это будет означать, что товар останется в пункте отправления. Поэтому на доставку товара из всех пунктов отправления фиктивному потребителю назначаются тарифы, равные стоимости хранения единицы груза либо стоимости его утилизации (если недоставленный товар не может быть в дальнейшем использован). Аналогично, на доставку товара от фиктивного поставщика во все пункты назначения назначаются тарифы, равные штрафу за недопоставку единицы продукции (поскольку доставка xijфикт. единиц товара в j-й пункт потребления от фиктивного по-

ставщика с номером i означает на практике, что j-му потребителю будет доставлено на xijфикт. единиц товара меньше, чем он запросил).

Обозначим через xij количество груза, планируемого к перевозке от

i-го поставщика j-му потребителю. При наличии баланса производства и потребления (4.1.1) математическая модель закрытой транспортной за-

дачи будет выглядеть так: требуется найти план перевозок

X = ( xij ), i =1, 2, …, m, j =1, 2, …, n ,

минимизирующий общую стоимость всех перевозок

при условии, что из любого пункта производства вывозится весь продукт:

133

j=1

илюбому потребителю доставляется необходимое количество груза:

ТЕОРЕМА. Закрытая транспортная задача всегда имеет решение.

Доказательство. Закрытая транспортная задача представляет собой задачу линейного программирования. При этом множество допустимых решений непусто, поскольку, например, допустимым решением, очевидно, является набор чисел

x11 0, x12 0, …, xmn 0 ,

Поскольку x11 0, x12 0, …, xmn 0 , минимизируемая целевая функция

m n

z = ∑∑cij xij i=1 j=1

ограничена снизу нулем на множестве допустимых решений. Таким образом, утверждение теоремы доказано.

ТЕОРЕМА. Ранг матрицы коэффициентов системы уравнений

(4.1.3)—(4.1.4) равен m + n −1.

134

Доказательство. Запишем систему уравнений (4.1.3)—(4.1.4) в развернутом виде:

сумма последних n строк равна

Вычтем из суммы первых m строк сумму последних n строк, получим нулевую строку, так как транспортная задача закрытая и

135

Таким образом, ранг матрицы системы ограничений закрытой транспортной задачи меньше m + n .

Рассмотрим теперь линейную комбинацию первых m + n −1 строк матрицы системы, взятых с коэффициентами α1, α2 , …, αm , αm+1, αm+2 , …,

αm+n−1 . Чтобы она обращалась в нуль, должны выполняться следующие равенства:

α1 + αm+1 = 0, α1 + αm+2 = 0, α1 + αm+n−1 = 0, α1 = 0,

α2 + αm+1 = 0, α2 + αm+2 = 0, α2 + αm+т−1 = 0, α2 = 0,

αm + αm+1 = 0, αm + αm+2 = 0, αm + αm+т−1 = 0, αm = 0,

рицы системы не меньше m + n −1.

Итак, ранг матрицы системы ограничений закрытой транспортной задачи равен m + n −1, поскольку он меньше m + n , но не меньше m + n −1.

Утверждение теоремы доказано. Поскольку число неизвестных в закрытой транспортной задаче рав-

но mn, а ранг системы ограничений равен m + n – 1, оптимальное решение закрытой транспортной задачи, как правило, неединственно.

Рассмотрим постановку задачи, двойственной к закрытой транспортной задаче (4.1.2)—(4.1.5). Каждому ограничению (4.1.3) по-

ставим в соответствие двойственную переменную pi (i =1, 2,…, m) , каждому ограничению (4.1.4) — двойственную переменную q j ( j =1, 2, …, n) .

При этом, поскольку ограничения (4.1.3), (4.1.4) представляют собой уравнения, переменные pi и q j могут принимать значения любого знака.

Задача, двойственная к задаче (4.1.2)—(4.1.5), имеет вид

ТЕОРЕМА. Задача, двойственная к транспортной, всегда имеет оптимальное решение.

Доказательство следует из того, что имеет решение исходная зада-

ча (4.1.2)—(4.1.5).

ТЕОРЕМА. Допустимое решение закрытой транспортной задачи

(4.1.2)—(4.1.5)

136

xij , i = 1, 2, …, m, j = 1, 2, …, n ,

и допустимое решение

pi , i = 1, 2, …, m, q j , j = 1, 2, …, n

задачи (4.1.6)—(4.1.7), двойственной к транспортной, являются оптимальными решениями соответствующих задач тогда и только тогда, когда

Доказательство. Согласно теореме о дополняющей нежесткости, для того чтобы допустимые решения транспортной задачи и задачи, двойственной к транспортной, были оптимальными, необходимо и достаточно выполнение следующих условий:

никаких ограничений на pi и q j . Существенными для переменных pi и q j

являются только условия (4.1.10). Для решения транспортной задачи применяется метод потенциа-

лов, который состоит из шагов. На первом шаге строится некоторый начальный план перевозок, т. е. выбирают произвольное базисное допустимое решение задачи (4.1.2)—(4.1.5). На каждом из последующих шагов проверяется оптимальность последнего найденного плана перевозок, и если план не оптимален, то производится перераспределение поставок с целью сокращения их суммарной стоимости — для этого по определенным правилам производится переход от одного базисного решения к другому. Каждый шаг метода потенциалов сопровождается заполнением т р а н с - п о р т н о й т а б л и ц ы (табл. 4.1.1), строки которой соответствуют поставщикам (в заголовках строк указываются запасы продукта у поставщиков ai), а столбцы соответствуют потребителям (в заголовках столбцов указываются запросы потребителей bj). В клетки транспортной таблицы заносятся п о с т а в к и продукта, перевозимого от соответствующего поставщика к соответствующему потребителю (xij). Кроме того, в правом верхнем углу каждой клетки указывается стоимость перевозки единицы продукта от соответствующего поставщика к соответствующему потребителю (cij).

137

По любой транспортной таблице можно восстановить соответствующий предпочитаемый эквивалент системы уравнений (4.1.3)—(4.1.4): в таблице записаны лишь правые части уравнений, причем номер клетки показывает, какая неизвестная в соответствующем уравнении является базисной.

Так как в системе (4.1.3)—(4.1.4) ровно m + n – 1 линейно независимых уравнений, то на каждом шаге в транспортной таблице должно быть ровно m + n – 1 занятых клеток.

Первое базисное допустимое решение легко построить по правилу северо-западного угла. В соответствии с этим правилом, заполнение транспортной таблицы начинается с левой верхней клетки («северо-западного угла») и состоит из однотипных шагов, на каждом из которых из рассмотрения исключается один поставщик или один потребитель:

∙если остаток продукта у i-го поставщика после предыдущих шагов меньше, чем неудовлетворенный запрос j-го потребителя, то исключается из рассмотрения i-й поставщик, и в клетку (i, j) заносится поставка xij, равная остатку продукта у i-го поставщика после предыдущих шагов;

∙если остаток продукта у i-го поставщика после предыдущих шагов больше, чем неудовлетворенный запрос j-го потребителя, то исключается из рассмотрения j-й потребитель, и в клетку (i, j) заносится поставка xij, равная неудовлетворенному запросу j-го потребителя;

∙если остаток продукта у i-го поставщика после предыдущих шагов равен неудовлетворенному запросу j-го потребителя, то исключается из рассмотрения или i-й поставщик, или j-й потребитель, и в клетку (i, j) заносится поставка xij = 0 равная остатку продукта у i-го поставщика после предыдущих шагов.

138

После этого рассматривается левая верхняя клетка среди тех, которые остаются после вычеркивания строк, соответствующих поставщикам, весь запас продукта у которых уже распределен по потребителям, и столбцов, соответствующих потребителям, запросы которых уже удовлетворены.

Существуют и другие методы построения начального плана перевозок (например, метод минимального элемента предполагает заполнение клеток не в направлении «северо-запад — юго-восток», а начиная с наименьшего транспортного тарифа). Однако эти методы при сколь-нибудь существенных размерах транспортных таблиц не дают существенного вычислительного выигрыша по сравнению с методом северо-западного угла.

Когда транспортная таблица содержит некоторое базисное допустимое решение транспортной задачи, начинают вычисление потенциалов.

Каждому поставщику ставится в соответствие п о т е н ц и а л pi, а

Один из потенциалов можно выбрать произвольно, так как в системе (4.1.3)—(4.1.4) одно уравнение линейно зависит от остальных. Обычно полагают p1 = 0 . Остальные потенциалы вычисляются из условия, что для базисных клеток ij = 0 .

Затем по формуле (4.1.9) вычисляются оценки всех свободных клеток. Если хотя бы одна из оценок строго положительна, то базисное допустимое решение, содержащееся в данной транспортной таблице, не является оптимальным. Выбирается свободная клетка (r, s), соответствующая наибольшей положительной оценке

rs = max( ij > 0) .

i, j

Для выбранной свободной клетки (r, s) строится цикл пересчета — замкнутая ломаная, одна из вершин которой находится в данной свободной клетке, а все остальные — в занятых клетках, соседние звенья взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы. Можно доказать, что для любой свободной клетки н е в ы р о ж д е н н о й закрытой транспортной задачи цикл пересчета всегда существует, является единственным и состоит из четного числа вершин.

Клетка (r, s) помечается знаком «плюс», далее соседние вершины цикла пересчета помечаются по очереди знаками «минус», «плюс». Выбирается минимальная из поставок, отмеченных знаком «минус» (ρmax), и к поставкам, отмеченным знаком «плюс», добавляется ρmax, а из поставок отмеченных знаком «минус», вычитается ρmax. Так производится перераспределение поставок вдоль цикла пересчета, при котором происходит та-

кой переход к новому базисному допустимому решению, что в клетку

139