Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие

и товаром Гиффина, если при увеличении цены этого товара спрос на него растет:

∂xi > 0 . ∂pi

Спрос на ценный товар обязательно падает при увеличении его цены: в правой части уравнения Слуцкого (6.4.2), записанного при j = i ,

уменьшаемое отрицательно согласно (6.4.3), а вычитаемое неотрицательно,

вара служит маргарин: потребитель приобретет меньше маргарина и в том случае, когда увеличится цена маргарина, и в том случае, когда увеличится богатство потребителя;

∙т о в а р ы Ги ф ф и н а, в качестве примера такого товара традиционно приводят картофель в Ирландии XIX в.: в то время бó льшая часть потребительских расходов населения тратилась на приобретение картофеля, но по мере увеличения богатства потребители предпочитали покупать больше мяса и меньше картофеля; при увеличении цены картофеля реальный доход потребителя уменьшался настолько, что он уже не могли покупать столько же мяса, как и прежде, и потому был вынужден увеличивать потребление картофеля.

Та бли ц а 6.4.1

201

Точно так же можно показать, что первый и третий, а также второй и третий товары образуют взаимозаменяемые пары, а взаимодополняющие товары для данного потребителя отсутствуют.

§ 6.5. МОДЕЛЬРЫНОЧНОГО РАВНОВЕСИЯ

Рассмотрим рынок n товаров с k участниками. Пусть вектор

рами. Для этого они должны ввести некоторую д е н е ж н у ю е д и н и ц у и определить в е к т о р р ы н о ч н ы х ц е н p = ( p1 p2 pn ) .

Если на рынке будут установлены некоторые цены товаров: p1, p2, …, pn, то начальное богатство каждого участника (до обмена) в денежном выражении определяется как

n

I j = px j = ∑ pl xlj , j =1, 2, …, k .

l =1

При этом суммарное предложение i-го товара на рынке будет равно суммарным запасам этого товара у всех участников:

k

QiS = ∑xij , i =1, 2, …, n .

j=1

Теперь можно для каждого участника поставить з а д а ч у п о - т р е б и т е л я и определить ф у н к ц и и с п р о с а участников рынка:

203

Таким образом, суммарный спрос всех участников на i-й товар будет равен

Согласно закону Вальраса р ы н о ч н о е р а в н о в е с и е определяется равенством суммарного спроса и суммарного предложения по каждому товару:

Можно показать, что одно из уравнений данной системы обязательно является следствием остальных, поэтому цены определяются из этой системы с точностью до коэффициента пропорциональности. Это очевидно: ведь цены зависят от выбора денежной единицы.

Таким образом, можно определить равновесное конечное распределение товаров между участниками рынка, подставив в функции спроса (6.5.1) равновесные цены, определенные из системы (6.5.2).

ПРИМЕР 6.5.1. Рассматривается рынок трех товаров. Требуется определить равновесное распределение товаров между четырьмя участниками рынка, если эти участники обладают одинаковыми функциями по-

лезности u(x1, x2 , x3 ) = 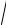x1x2 x3 , а начальные запасы товаров у участников рынка составляют

Функции спроса участников одинаковы, так как функция полезности у них одна и та же. Для данной функции полезности функция спроса (6.3.15):

204

была определена в примере 6.2.1.

Суммарный спрос на первый товар составляет

= ( p1 + 2 p2 + 3 p3 ) + (2 p1 + 2 p2 + 2 p3 ) + (3 p1 + 4 p2 + 5 p3 ) + ( p1 + p2 + 6 p3 ) =

3p1

=7 p1 + 9 p2 + 16 p3 , 3 p1

аналогично определяется суммарный спрос на второй и третий товары:

Суммарное предложение первого товара равно

Q1S = x11 + x12 + x13 + x14 = 1 + 2 + 3 + 1 = 7,

Q2S = x12 + x22 + x23 + x24 = 2 + 2 + 4 + 1 = 9,

Q3S = x31 + x32 + x33 + x34 = 3 + 2 + 5 + 6 = 16.

Запишем условие равенства суммарного спроса и суммарного предложения каждого товара:

Решение данной системы уравнений с помощью метода Жордана — Гаусса иллюстрируется табл. 6.5.1.

205

Т а бли ц а 6.5.1

Таким образом, общее решение системы для определения равновесных цен таково:

где, очевидно, цена третьего товара α > 0 . Ясно, что цены определяются относительно, поэтому для удобства положим p3 = α = 63 ден. ед., тогда

При таких ценах начальные запасы участников рынка определяют их богатство:

Теперь можно определить равновесное распределение товаров:

206

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1.Во сколько раз возрастет объем бюджетного множества при увеличении дохода в два раза?

2.Постройте несколько кривых равноценности для мультипликатив-

ной функции полезности двух товаров u(x1, x2 ) = x1α x2β (α, β > 0, α + β < 1) . Найдите предельные нормы замены и эластичности замены одного товара другим для этой функции.

3.Постройте несколько кривых равноценности для пропорциональной функции полезности двух товаров u(x1, x2 ) = min{x1, 2x2}. Найдите предельные нормы замены и эластичности замены одного товара другим для этой функции.

4.Найдите функцию спроса потребителя, обладающего линейной функцией полезности u ( x1, x2 ) = a1x1 + a2 x2.

5.Найдите функцию спроса потребителя, обладающего пропорциональной функцией полезности u(x1, x2 ) = min{x1, 2x2}.

6.Найдите функцию спроса потребителя, обладающего мультиплика-

тивной функцией полезности u(x1, x2 ) = 3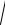 x1x2 .

7.Какой смысл имеет множитель Лагранжа λ в задаче определения потребительского спроса?

8.Убедитесь, что уравнение Слуцкого действительно выполняется для функции полезности u(x1, x2 ) = 3 x1x2 .

9.Составьте уравнение Слуцкого для пропорциональной функции полезности двух товаров u(x1, x2 ) = min{x1, 2x2} .

207

10.Найдите состояние равновесия на рынке, если функция спроса

D( p) = a − bp , а функция предложения S( p) = −c + dp (p — цена товара, a, b, c, d > 0 — константы).

11.Каков содержательный смысл конкурентного равновесия в модели Вальраса?

12.Проверьте выполнение закона Вальраса на рынке с тремя участниками, имеющими одинаковые функции полезности u(x1, x2 , x3 ) =

(n + 1)-го товара выступают деньги, т. е. pn+1 = 1. Функция полезности набора товаров совпадает с его стоимостью. Найдите предельные полезности первых n товаров и предельные нормы замещения первых n товаров деньгами.

14.Убедитесь, что уравнение Слуцкого действительно выполняется для функции полезности u(x1, x2 ) = 3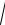 x1x2 .

208

ГЛАВА 7. ЗАДАЧИДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ ВЭКОНОМИКЕ

§ 7.1. ПОСТАНОВКА ЗАДАЧИ ДИНАМИЧЕСКОГОПРОГРАММИРОВАНИЯ

Динамическое программирование представляет собой математиче-

ский аппарат, разработанный для решения некоторого класса задач математического программирования путем их разложения на относительно небольшие и, следовательно, менее сложные задачи. Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления планируемая операция разделяется на ряд последовательных ш а г о в или э т а п о в. Соответственно и сам процесс планирования операции становится м н о г о ш а г о в ы м и развивается последовательно, от этапа к этапу, причем каждый раз оптимизируется управление только на одном шаге.

Некоторые операции естественно распадаются на этапы, в других это деление приходится вводить искусственно. Примером «естественно многоэтапной» операции может служить планирование работы предприятия на некоторый период времени, состоящий из нескольких хозяйственных лет или кварталов.

Состояние системы на каждом шаге i = 1, 2, …, n характеризуется некоторой переменной — параметром состояния xi , который зависит от свое-

Наилучший эффект на данном этапе вместе с уже рассмотренными шагами характеризуется функцией состояния. Решение конкретной задачи методом динамического программирования сводится к выбору параметра состояния (что требует определенного навыка), составлению функции состояния и рекуррентных соотношений, связывающих функции состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления.

209

Принцип динамического программирования предполагает, что управление на каждом шаге должно выбираться с учетом всех его последствий в будущем. Однако из этого правила есть исключение. Среди всех шагов существует один, который может планироваться «без оглядки на будущее» — это последний шаг. Спланировав оптимальным образом этот последний шаг, можно к нему «пристраивать» предпоследний, затем предыдущий и т. д.

Поэтому процесс динамического программирования разворачивается от конца к началу. Сначала делаются различные предположения о том, чем кончился предпоследний шаг, и для каждого из них выбирается управление на последнем. Затем делаются различные предположения о том, чем кончился предпредпоследний шаг, т. е. рассматриваются различные состояния системы на третьем от конца шаге и выбирается управление на втором от концы шаге так, чтобы оно вместе в уже выбранным управлением на последнем шаге обеспечивало наилучший эффект на двух последних шагах, и так далее, вплоть до первого от начала шага, с которого начинался процесс.

В начале процесса состояние системы нам известно, и делать какие-то предположения не нужно. Поэтому, имея в виду, что все последующие шаги спланированы для различных состояний системы, остается выбрать управление на первом шаге так, чтобы оно было оптимальным с учетом всех управлений, уже принятых наилучшим образом на всех последующих шагах.

Принцип, положенный в основу построения такого решения (искать всегда оптимальное продолжение процесса относительно того состояния, которое достигнуто в данный момент), принято называть принципом оп-

тимальности.

§ 7.1. ЗАДАЧА ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯИНВЕСТИЦИЙ

Знакомство с методом динамического программирования проще всего начать с рассмотрения нелинейной задачи распределения ресурсов между предприятиями одного производственного объединения или отрасли. Для определенности можно считать, что речь идет о распределении капитальных вложений.

Предположим, что производственный холдинг состоит из n предприятий, и на их развитие выделены инвестиции в размере b ден. ед. Обозначим через zi (x) прирост мощности или прибыли на i-м предприятии, если оно получит инвестиции в размере x ден. ед. В динамической задаче распределе-

ния инвестиций требуется найти такое распределение

u1 u = u2un

210