
Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие
.pdf
Microsoft Excel. Отчет о результатах
Результат: Решение найдено. Все ограничения и условия оптимальности выполнены. Модуль поиска решения
Модуль: Поиск решения нелинейных задач методом ОПГ Время решения: 0,01 секунд.
Число итераций: 3 Число подзадач: 0
Параметры поиска решения
Максимальное время Без пределов, Число итераций Без пределов, Precision 0,000001
Сходимость 0,0001, Размер совокупности 100, Случайное начальное значение 0, Центральные производные Максимальное число подзадач Без пределов, Максимальное число целочисленных решений Без пределов, Целочисленное отклонение 1%, Считать неотрицательными
Ячейка целевой функции (Максимум) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Ячейка |
Имя |
|
Исходное значение |
Окончательное значение |
|
|
|
|
|
|||||||
|
|
$B$3 |
f(x1, x2) = |
|
|
|
–128 |
|
|
–28,9 |
|
|
|
|
|
|||
Ячейки переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Ячейка |
Имя |
|
Исходное значение |
Окончательное значение |
Целочисленное |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$B$1 |
x1 = |
|
|
|
|
0 |
|
|
2,9 |
|
Продолжить |
|
|
|
||
|
|
$B$2 |
x2 = |
|
|
|
|
0 |
|
|
6,3 |
|
Продолжить |
|
|
|
||
Ограничения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Ячейка |
Имя |
|
Значение ячейки |
|
Формула |
Состояние |
|
Допуск |
|
|||||||
|
|
$B$4 |
φ1(x1, x2) = |
|
|
|
|
15 |
$B$4<=$B$6 |
|
|
|
Привязка |
0 |
|
|||
|
|
$B$5 |
φ1(x1, x2) = |
|
|
|
|
9,2 |
$B$5<=$B$7 |
|
|
|
Без привязки |
0,8 |
|
|||
|
|
|
|
|
|
б) отчет о результатах |
|
|
|
|
|
|||||||
|
|
|
|
Microsoft Excel. Отчет об устойчивости |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Ячейки переменных |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Окончательное |
Приведенный |
|
|
|
|
||||
|
|
|
|
|
Ячейка |
Имя |
|
значение |
градиент |
|
|
|
||||||
|
|
|
|
|
$B$1 |
x1 = |
|
|
2,9 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
$B$2 |
x2 = |
|
|
6,3 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Ограничения |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Окончательное |
Лагранжа |
|
|
|
|
||||
|
|
|
|
|
Ячейка |
Имя |
|
значение |
множитель |
|
|
|
||||||
|
|
|
|
|
$B$4 |
φ1(x1, x2) = |
|
15 |
|
|
|
3,4 |
|
|
|
|
||
|
|
|
|
|
$B$5 |
φ1(x1, x2) = |
|
9,2 |
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
в) отчет об устойчивости |
|
|
|
|
|
|||||||
Microsoft Excel. Отчет о пределах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Целевая функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Ячейка |
Имя |
|
Значение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$B$3 |
f(x1, x2) = |
|
|
–28,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Переменная |
|
|
Нижний |
Целевая функция |
Верхний Целевая функция |
|
|||||||||
|
|
Ячейка |
Имя |
|
Значение |
предел |
Результат |
предел |
Результат |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$B$1 |
x1 = |
|
|
2,9 |
|
|
0 |
|
–66,89 |
|
|
2,9 |
|
–28,9 |
|
|
|
|
$B$2 |
x2 = |
|
|
6,3 |
|
|
0 |
|
–90,01 |
|
|
6,3 |
|
–28,9 |
|
|
г) отчет о пределах
Рис. 5.6.5. Отчеты о результатах, устойчивости и пределах, полученные с помощью надстройки «Поиск решения»
182



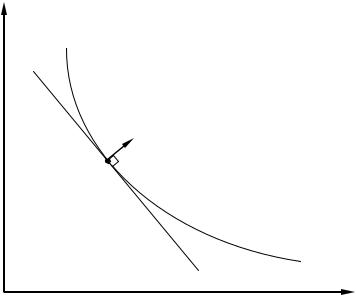
x2
u(x1 , x2 )=u0 =const
gradu(x1 , x2 ) |
x1
0
Рис. 6.2.2. Поверхность безразличия и градиент функции полезности
Чтобы старый и новый наборы товаров оказались на одной поверхности безразличия, необходимо выполнение условия (6.2.2). Учтем, что dxk = 0 при k ¹ i, k ¹ j , тогда получим, что
|
|
∂u |
dx |
+ |
|
∂u |
dx |
|
= 0 , |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
∂xi |
|
∂x j |
j |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx j |
= − |
|
∂u / ∂x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
i |
. |
|
|
|
||||||||
|
|
|
dx |
∂u / ∂x |
|
|
||||||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
j |
|
|
||||
Величина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r j = lim |
|
x j |
|
|
= − |
dx j |
|
= |
∂u / ∂xi |
. |
||||||||||
|
|
|
|
|
|
|
||||||||||||||
i |
xi |
→0, − x |
|
|
|
|
|
dx |
|
|
|
∂u / ∂x |
|
|
||||||
|
|
|
|
|
|
|
|
|
j |
|||||||||||
|
u ( x)=const |
i |
|
|
|
|
|
|
i |
|
|
|
|
|||||||
называется предельной нормой замены i-го товара j-м; она показывает, на сколько е д и н и ц должно увеличиться количество j-го товара, чтобы к о м п е н с и р о в а т ь потерю единицы i-го товара (т. е. чтобы полезность набора товаров не изменилась).
Часто бывает удобно иметь дело не с абсолютными величинами, а с о т н о с и т е л ь н ы м и. Эластичность замены i-го товара j-м ( eij ) показывает, на сколько п р о ц е н т о в должно увеличиться количество j-го товара, чтобы компенсировать уменьшение количества i-го товара на 1%:
e j = lim |
|
x j |
/ x j |
= − |
xi |
lim |
x j |
= |
xi |
r j = |
xi |
|
∂u / ∂xi |
. |
|||||
|
|
|
|
|
|
|
|
||||||||||||
i |
xi →0, |
− |
x / x |
|
x |
|
xi →0, |
x |
|
x |
|
i |
x |
|
|
∂u / ∂x |
|
|
|
|
|
|
|
j |
|
j |
|
j |
|||||||||||
|
u ( x)=const |
|
i |
i |
|
|
j u ( x)=const |
i |
|
|
|
|
|
|
|||||
190

