
Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие
.pdfчитаемая сумма zk 1 + zk 2 + + zkn представляет количество вещества, вытекающего из вершины X k по всем выходящим из этой вершины дугам (также
zkl = 0 , если нет дуги ( X k , X l ) .
Таким образом, ограничения (8.3.2) означают, что количество вещества, притекающего в произвольную точку сети (кроме X 0 и X n ), равно количеству вещества, вытекающего из этой точки. Поток, удовлетворяющий ограничениям (8.3.1) и (8.3.2), будем называть допустимым.
Из ограничений (8.3.2) также следует, что общее количество вещества
n |
|
|
∑ z0 j , вытекающего из вершины X 0 |
(входа сети), совпадает с общим количе- |
|
j=1 |
|
|
n−1 |
|
|
ством вещества ∑ zin , притекающего в вершину X n |
(выход сети), т. е. |
|
i=0 |
|
|
n |
n−1 |
|
∑z0 j |
= ∑zin = w. |
(8.3.3) |
j=1 |
i=0 |
|
Линейная функция w называется величиной потока в сети.
Таким образом, задача о максимальном потоке в сети представляет собой задачу линейного программирования: среди всех решений системы линейных ограничений (8.3.1)—(8.3.2) следует найти такое решение, которое максимизирует линейную форму (8.3.3). Это решение zij называется
максимальным потоком в сети.
Как и любая задача линейного программирования, она может быть решена одним из известных методов линейного программирования. Но в силу специфики задачи ее легче решить специальными методами.
Введем некоторые дополнительные понятия. Разобьем множество всех вершин сети на два непересекающихся подмножества P и Q так, чтобы X 0 P , a X n Q . Сечением (P, Q) сети назовем совокупность всех дуг
( Xi , X j ) , концы которых принадлежат разным подмножествам. Каждому сечению (P, Q) поставим в соответствие число C (P,Q) — пропускную способность сечения, — равное сумме пропускных способностей всех дуг сети, начинающихся в P и кончающихся в Q, т. е.
C(P,Q) = ∑ cij .
X i P
X j Q
Любой путь из X 0 в X n обязательно содержит хотя бы одну дугу сечения (P, Q) , которая начинается в P и кончается в Q . Но пропускная способность пути не превышает пропускной способности каждой его дуги. Поэтому величина любого потока из X 0 в X n , являющаяся суммарной пропускной способностью всех путей из X 0 в X n , не может превысить пропускной способности любого сечения (P, Q) , т. е. всегда
242
пути дуге ( Xi , X j ) , надо считать равной c′ji = c ji + θ . Это следует из того,
что дуга ( X j , Xi ) не препятствует доставке в X i количества cji вещества по
новому пути с использованием этой дуги плюс количества θ по части старого пути от X 0 до X i без использования этой дуги (так как пропускная
способность всех дуг старого пути не меньше θ). Мы учитываем, что X i те-
перь соединена с X 0 двумя путями, т. е. получается, что дуга ( X j , Xi ) как бы заменена новой дугой с увеличенной пропускной способностью c ji + θ .
Таким образом, процесс отыскания максимального потока в сети сводится к следующим действиям.
1. Построить произвольный путь μ из X 0 в X n , идущий по н е н а -
с ы щ е н н ы м дугам.
2.Определить пропускную способность θμ найденного пути как наименьшую из пропускных способностей дуг этого пути
θμ = min{cμ}; |
(8.3.4) |
ij |
|
3.Вычислить новые пропускные способности всех дуг данного пути:
μ |
= c |
μ |
μ |
(8.3.5) |
c |
|
− θ ; |
||
ij |
ij |
|
|
|
4.Вычислить новые пропускные способности всех тех дуг, которые симметричны дугам данного пути
μ |
= c |
μ |
+ θ |
μ |
(8.3.6) |
|
c |
ji |
ji |
; |
|||
|
|
|
|
|
||
5.Процесс, описанный в пп. 2—4, продолжается до тех пор, пока удается построить путь из X 0 в X n , идущий по ненасыщенным дугам. Если
такой путь построить нельзя, то это означает, что из источника X 0 в сток пропущен максимальный поток. Затем следует вычесть пропускную способность соответствующей дуги исходной сети. П о - л о ж и т е л ь н ы е значения найденных разностей определяют величины потоков по дугам в максимальном потоке данной сети, а величина максимального потока в сети равна
n |
n−1 |
w = ∑zoj |
= ∑zin . |
j=1 |
i=0 |
В заключение подчеркнем еще раз, что процесс преобразований прекращается, как только будет получена сеть, в которой нельзя построить ни одного пути из X 0 в X n , идущего по ненасыщенным дугам.
Покажем, что полученный таким образом поток является максимальным. Для этого построим в последней сети сечение (P, Q) следующим образом. Ко множеству P отнесем источник X 0 и все те вершины, которые достижимы из X 0 по какому-нибудь пути, составленному из нена-
244
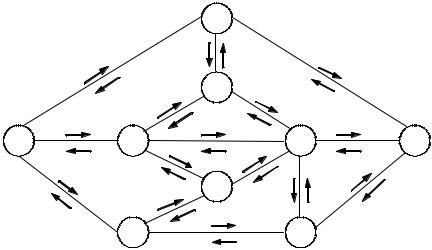
т. е. дуга ( X 5 , X 8 ) |
становится насыщенной, а пропускные способности дуг, |
||||||
симметричных дугам пути, увеличиваются на 2 единицы: |
|||||||
c′ |
= c |
50 |
+ θ = 4 + 2 = 6, c′ |
= c |
85 |
+ θ = 2 + 2 = 0 . |
|
50 |
|
1 |
85 |
|
1 |
||
Сеть с новыми пропускными способностями дуг приведена на рис. 8.3.2, а.
Теперь находим новый путь из X 0 вX8 , проходящий по ненасыщенным дугам, например, μ 2 = { X 0 , X 5 , X 4 , X 6 , X 8 } , определяем
θ2 = min{c05 , c54 , c46 , c68 } = min{3, 3, 1, 6} = 1
ипропускаем по этому пути поток величиной в одну единицу. Меняем пропускные способности дуг этого пути и симметричных им дуг:
c′′ |
= c′ |
− θ |
2 |
= 3 − 1 = 2, c′′ |
= c′ |
+ θ |
2 |
= 6 + 1 = 7, |
|||
05 |
05 |
|
|
|
50 |
50 |
|
|
|
||
c′′ |
= c′ |
− θ |
2 |
= 3 |
− 1 |
= 2, c′′ |
= c′ |
+ θ |
2 |
= 3 + 1 = 4, |
|
54 |
54 |
|
|
|
45 |
45 |
|
|
|
||
c′′ |
= c′ |
− θ |
2 |
= 1 − 1 = 0, c′′ |
= c′ |
+ θ |
2 |
= 1 + 1 = 2, |
|||
46 |
46 |
|
|
|
64 |
64 |
|
|
|||
c′′ |
= c′ |
− θ |
2 |
= 6 |
− 1 |
= 5, c′′ |
= c′ |
+ θ |
2 |
= 2 + 1 = 3. |
|
68 |
68 |
|
|
|
86 |
86 |
|
|
|
||
Дуга ( X 4 , X 6 ) становится насыщенной. Сеть с измененными про-
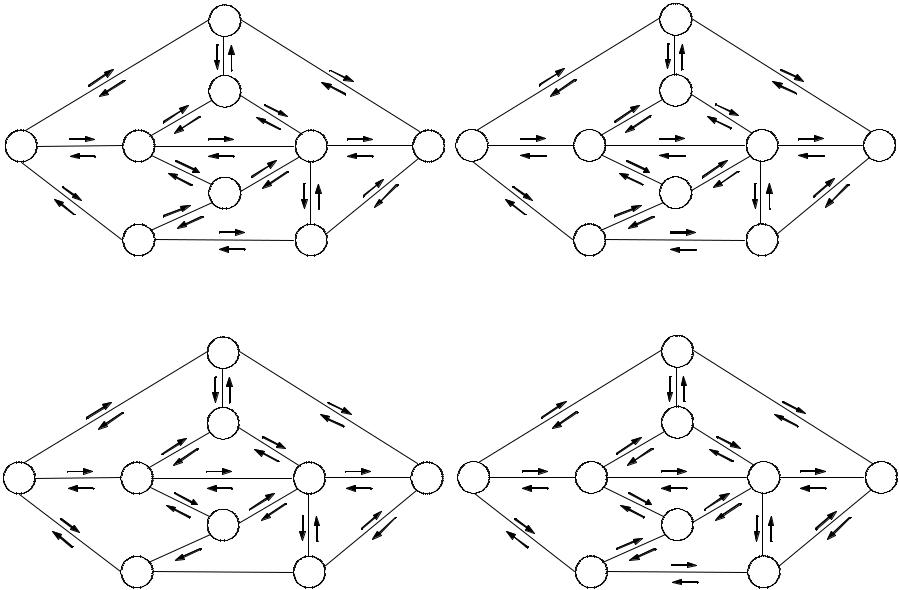
пускными способностями приведена на рис. 8.3.2, б. |
|
|
|||||
Далее последовательно находим пути μ3 , μ4 , μ5 , μ6 |
и по ним пропус- |
||||||
каем потоки величиной θ3 , θ4 , θ5 , θ6 |
соответственно: |
|
|
||||
μ3 = { X 0 , X 5 , X 4 , X 1 , X 6 , X 8 }, |
θ3 |
= min{2, 2, 1, 2, |
5} = 1 |
(рис. 8.3.2, в), |
|||
μ 4 |
= { X 0 , X 1 , X 6 , X 8 }, |
θ4 |
= min{1, 1, |
4} = 1 |
(рис. 8.3.2, г), |
||
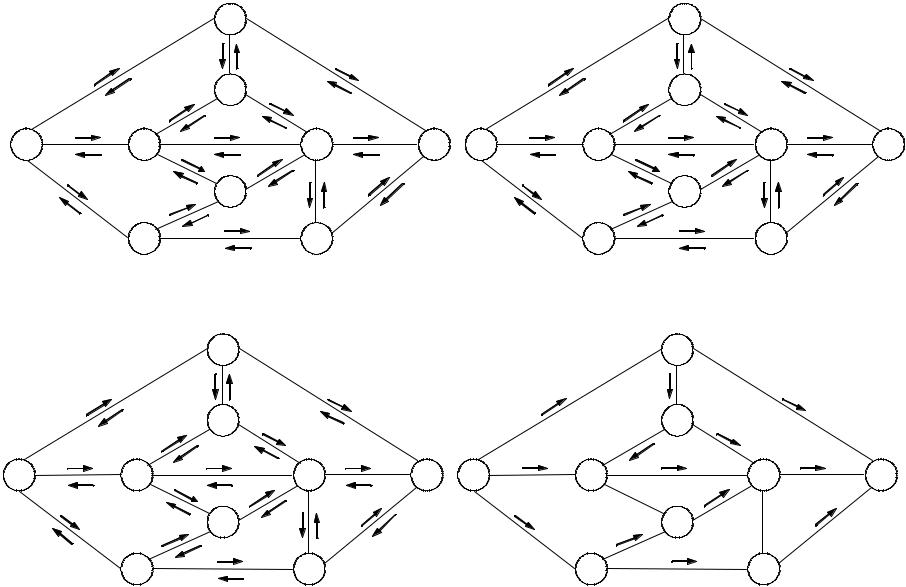
μ5 |
= { X 0 , X 2 , X 7 , X 8 }, |
θ5 = min{4, |
3, |
2} = 2 |
(рис. 8.3.2, д), |
||
μ 6 = { X 0 , X 2 , X 3 , X 6 , X 8 }, |
θ6 |
= min{2, |
2, |
3, 3} = 2 (рис. 8.3.2, е). |
|||
На указанных в скобках рисунках приведены сети, полученные после соответствующих преобразований на каждом шаге. В сети, изображенной на рис. 8.3.2, е, уже нельзя указать ни одного пути, идущего из X 0 в X8 по ненасыщенным дугам. Следовательно, процесс преобразований закончен.
Чтобы определить максимальный поток, вычитаем от пропускных способностей дуг исходной сети (рис. 8.3.1) измененные пропускные способности тех же дуг последней сети (рис. 8.3.2, е). Результат приведен на рис. 8.3.2, ж.
Положительные значения найденных разностей дают нам величины zij потоков по соответствующим дугам ( X i , X j ) в максимальном потоке из
источника X 0 в сток X8 .
Искомый максимальной поток приведен на рис. 8.3.2, з, где числа, стоящие у каждой дуги, показывают величину потока по данной дуге, а стрелки — направление потока по этой дуге.
246
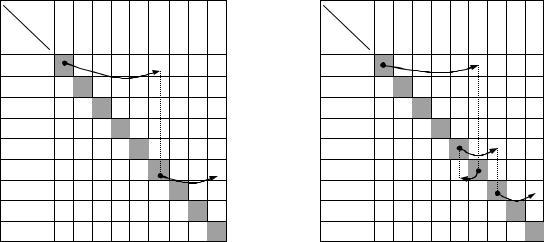
Таким образом, по таблице мы нашли путь, ведущий по ненасыщенным дугам из источника в сток:
X 0 → X 5 → X 6 .
Теперь по таблице надо указать пропускную способность найденного пути и изменить пропускные способности дуг этого пути и симметричных им дуг. Для этого отмечаем знаком «минус» числа в тех клетках, где находятся концы дуг, а числа в клетках, симметричных указанным относительно главной диагонали, отмечаем знаком «плюс».
Пропускная способность найденного пути равна, очевидно, наименьшему среди чисел, отмеченных знаком «минус»:
θ = min{cij−}.
В данном случае θ1 = 2 .
Чтобы вычислить новые пропускные способности дуг найденного пути и симметричных им дуг, достаточно, согласно (8.3.5) и (8.3.6), из всех чисел, отмеченных знаком «минус», вычесть наименьшую пропускную способность θ1 , а ко всем числам, отмеченным знаком «плюс», прибавить θ1 . Получаем табл. 8.3.2 с измененными пропускными способностями дуг сети. Она соответствует рис. 8.3.1, а. По таблице находим путь
X 0 → X 5 → X 4 → X 6 → X 8 ,
отмечаем знаком «минус» пропускные способности дуг этого пути (они записаны в клетках на концах стрелок), знаком «плюс» — пропускные способности симметричных дуг. Находим θ2 как наименьшее среди
Прибавляя θ2 к cij+ и вычитая из cij− , переходим к табл. 8.3.3 и т. д.
Выполнив еще четыре шага, придем к табл. 8.3.4. Из этой таблицы видно, что не существует ни одного пути из источника в сток. Действительно, из X0 можно перейти в X5. Далее, так как в пятой строке только два ненулевых элемента c50 и c54, можно перейти либо в X0 (вернуться, что бессмысленно), либо в X4. Но в четвертой строке только один элемент c45, отличный от нуля. Поэтому из вершины X4 можно перейти только в X5, т. е. опять появляется контур. Никаких других возможностей нет. Следовательно, увеличить поток нельзя.
Для определения полученного максимального потока вычитаем из элементов первой таблицы (см. табл. 8.3.1) соответствующие элементы последней (см. табл. 8.3.4). Записывая только положительные из найденных разностей, получаем табл. 8.3.5, указывающую максимальный поток в заданной сети с величиной w* = z58 + z68 + z78 = 2 + 5 + 2 = 9 .
250

 0
0
 2
2