Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие

дится сопряженная переменная y(t), строится функция Гамильтона (12.2.7), определяются функции u(t), x(t), y(t), удовлетворяющие условиям (12.2.8)—(12.2.10), и из участков управлений u(t), доставляющих гамильтониану максимум при каждом t, формируется оптимальная управляющая траектория.

Принцип максимума дает необходимые, но, вообще говоря, не достаточные условия для существования максимума в задаче оптимального управления.

Однако в о п р е д е л е н н ы х ч а с т н ы х с л у ч а я х условия принципа максимума являются необходимыми и достаточными услови-

ями оптимальности.

Приведем без доказательства два таких частных случая:

∙когда гамильтониан линеен относительно управляющих параметров

(д о с т а т о ч н ы е у с л о в и я Р о з о н о е р а);

∙когда максимум гамильтониана представляет собой выпуклую

вверх функцию по фазовым координатам (д о с т а т о ч н ы е

ус л о в и я М а н г а с а р я н а).

§12.3. МОДЕЛИРОВАНИЕ ОПТИМАЛЬНОГОЭКОНОМИЧЕСКОГО РОСТА

Опишем модель национальной экономики, предложенную в 1956 г. Р. Солоу, Нобелевским лауреатом 1987 г. в области экономики.

В замкнутой односекторной экономической системе производится один универсальный продукт, который может как потребляться, так и инвестироваться. О с н о в н ы е п р е д п о л о ж е н и я м о д е л и С о л о у состоят в постоянстве темпа прироста числа занятых, износа основных производственных фондов и нормы накопления, отсутствии лага (т. е. запаздывания) капиталовложений.

∙к а п и т а л о м (основными фондами) K (t) ;

Пусть г о д о в о й т е м п п р и р о с т а ч и с л а з а н я т ы х составляет ν, тогда за промежуток времени dt численность занятых изменяется на величину dL = νL(t)dt , значит, для L(t) можно записать дифференциальное уравнение

dL = νL(t) , dt

341

решением которого является функция

L(t) = L0 eνt ,

где L0 — число занятых в начальный момент времени.

Пусть за год выбывает (изнашивается и приходит в негодность) доля μ основных производственных фондов, н о р м а н а к о п л е н и я составляет ρ, а годовой валовый внутренний продукт определяется л и -

по формуле производной частного. Имеем:

342

поэтому

= −(μ + ν)k(t) + ρF (k(t),1),

т. е. для фондовооруженности k(t) справедливо дифференциальное уравнение

dk = −(μ + ν)k(t) + ρF (k(t),1). dt

Рассмотрим в качестве производственной функции функцию Кобба — Дугласа F (K , L) = AK αL1−α , при этом F (k ,1) = Ak α .

Введя обозначения λ = μ + ν , f (k ) = F (k,1) = Ak α , получаем окон-

чательно модель Солоу в относительных показателях:

dkt = −λkt + ρf (k (t)),

dt

k0 = K0 / L0 ,

x(t) = f (k (t)), i(t) = ρf (k (t)), c(t) = (1 −ρ) f (k (t)).

Говорят, что экономика находится на стационарной траектории, если относительные показатели не меняются во времени. Поскольку x(t), i(t), и c(t) являются функциями от k(t), то для того, чтобы экономика находилась на стационарной траектории, необходимо и достаточно постоянства во времени фондовооруженности k(t), т. е.

dk = 0 или −λk + ρf (k ) = 0 . dt

Подставим сюда f (k ) = Ak α , получим условие стационарности траектории:

−λk +ρAkα = 0 .

Вынесем k α за скобку:

k α (−λk1−α + ρA)= 0 .

343

Из последнего уравнения видно, что возможны две стационарные

траектории экономики: вырожденная [когда k = 0, при этом x = Ak α = 0 , i = ρAk α = 0 , c = (1 − ρ) Ak α = 0 ] и невырожденная [когда −λk1−α +ρA = 0 ].

Из условия −λk1−α + ρA = 0 k1−α = ρA / λ следует, что на невырожденной стационарной траектории постоянные значения относительных показателей равны

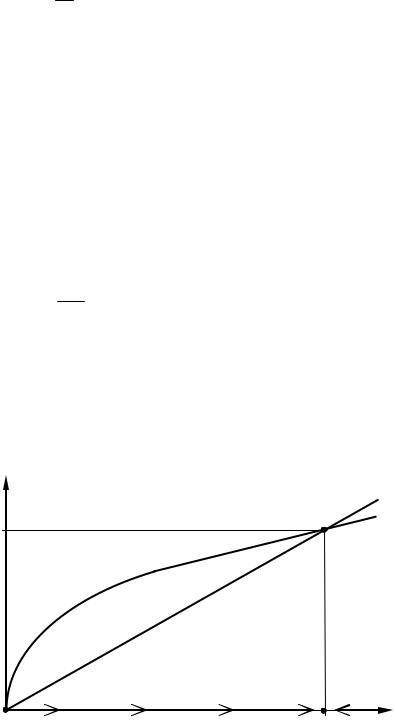
Исследуем, что произойдет, если экономика отклонится от стационарной траектории. Изобразим на рис. 12.3.1 графики функций λk и ρAk α [здесь α (0,1) ].

Рассмотрим вначале вырожденную стационарную траекторию

(на ней k(t) = 0). Если k(t) станет чуть больше нуля, то, как видно из рис. 12.3.1, ρAk α > λk , поэтому производная

dk = −λk +ρAkα > 0 , dt

откуда следует, что фондовооруженность k(t) будет возрастать. При этом dk / dt остается положительной при всех k (t) (0, k ) , поэтому вырожденная стационарная траектория является неустойчивой: достаточно малейшего возмущения, и k(t) начинает возрастать в сторону k = k ; при k(t) = k производная dk / dt становится равной нулю, т. е. k(t) kt перестает меняться.

λk, ρAkα

λk =A(k )α

λk

k

Рис. 12.3.1. Исследование устойчивости стационарных траекторий экономики в модели Солоу

344

Если экономика находится на невырожденной стационарной тра-

ектории k(t) = k , и произошло незначительное отклонение фондовооруженности в л е в о от стационарного значения k , то, как мы уже убедились, k(t) начинает возрастать до тех пор, пока вновь не вернется к значению k . Если же k(t) отклонится от k в п р а в о, то, как показывает рис. 12.3.1, ρA(k (t))α < λk (t) , поэтому производная

dk = −λk(t) +ρA(k(t))α < 0 , dt

значит, k(t) будет убывать до тех пор, пока не станет равной k . Таким образом, невырожденная стационарная траектория

является у с т о й ч и в о й: при любом отклонении от этой траектории экономика стремится к ней вернуться.

Данная невырожденная стационарная траектория носит название

траектории сбалансированного устойчивого экономического роста: чис-

ленность занятых на ней возрастает экспоненциально: L(t) = L0 eνt (конечно, при положительном темпе прироста занятых ν), а все относительные показатели постоянны, значит, все абсолютные показатели возрастают

пропорционально численности занятых L(t).

Рассмотрим теперь простейшую задачу управления экономикой, которая описывается моделью Солоу: попытаемся подобрать такую норму накопления ρ, чтобы удельное потребление на стационарной траектории сбалансированного устойчивого экономического роста было максимальным.

ЗОЛОТОЕ ПРАВИЛО НАКОПЛЕНИЯ. Чтобы удельное потребление на ста-

ционарной траектории сбалансированного экономического роста было максимальным, норма накопления ρ должна быть равна эластичности выпуска по фондам α .

Доказательство. Рассмотрим удельное потребление на стационарной траектории c как функцию нормы накопления:

и поставим задачу определения такой нормы накопления ρ, чтобы

c (ρ) → max

или, расписывая c (ρ) подробно,

345

В точке максимума первая производная должна быть равна нулю (или не существовать), а вторая производная должна быть отрицательной. В данном случае имеем:

изводная d 2c (ρ) / dρ2 < 0 , т. е. точка ρ = α является точкой м а к с и м у - м а удельного потребления, что и требовалось доказать.

Этот результат получен в 1966 г. Э. Фелпсом.

ПРИМЕР 12.3.1. Даны значения параметров A = 103 и α = 0,5 производственной функции Кобба — Дугласа. В модели Солоу с этой производственной функцией требуется рассчитать значения фондовооруженности, производительности труда и удельного потребления на стационарной траектории сбалансированного устойчивого экономического роста, на которой норма накопления равна ρ = 0, 2 , коэффициент выбытия основных производственных фондов за год составляет μ = 0, 2 , а годовой темп прироста численности занятых равен ν = 0, 05 . Сравнить полученное значение удельного потребления с оптимальным.

РЕШЕНИЕ. На стационарной траектории, соответствующей норме накопления ρ = 0, 2 , фондовооруженность

346

средняя производительность труда

x = A(k )α =10(64 ×104 )0,5 = 8 ×105 ,

удельное потребление

c = (1 - r)x = (1 - 0, 2)8 ×105 = 64 ×104 .

Согласно золотому правилу накопления, для того чтобы на стационарной траектории сбалансированного устойчивого экономического роста удельное потребление было максимальным, нужно выбрать норму накопления ρ равной эластичности выпуска по фондам α , т. е. в рассматриваемом примере максимум удельного потребления на стационарной траектории достигается при r = a = 0,5 . При этом

c = (1 - r )x = (1 - r ) A(k )α = (1 - 0,5) ×103 × (4 ×106 )0,5 =106 64 ×104.

Видим, что оптимальный выбор нормы накопления приводит к существенному увеличению удельного потребления на стационарной траектории — более чем в полтора раза!

Будем теперь считать, что норма накопления не является константой, а изменяется во времени. Для этого удобнее всего представить инвестиции в основные производственные фонды в виде разности валового продукта и валового потребления. Уравнение (12.3.1) в таком случае

dt

Переход в (12.3.2) к относительным показателям дает

dk = -lk(t) + f (k(t)) - c(t). dt

Модель оптимального экономического роста предполагает максимизацию интегрального дисконтированного (по непрерывной ставке δ) удельного потребления

347

при условиях

Горизонт планирования T в данной задаче может быть конечным или бесконечным. В случае планирования на конечный период в максимизируемый целевой функционал (12.3.3) целесообразно добавить слагаемое, накладывающее условие на минимальную фондовооруженность к концу периода [0, T].

Модель (12.3.3)—(12.3.4) представляет собой задачу оптимального управления, фазовой переменной в которой выступает фондовооруженность k(t), а управляющей переменной— удельное потребление c(t). На управление накладывается очевидное ограничение:

348

Общее решение уравнения (12.3.6) имеет вид m(t) = e−∫( f ′(k (t ))−(λ+δ))dt , поэтому, очевидно, m(t) > 0.

Гамильтониан

H(t, k (t), c(t), y(t)) = c(t) e−δt + m(t) e−δt (−λk (t) + f (k (t)) − c(t)) =

=((1 − m(t))c(t) + m(t)( f (k (t))− λk (t)))e−δt

при m(t) ¹ 1 линейно зависит от управления c(t), поэтому максимум гамильтониана по управляющей переменной c(t) может достигаться только

При m(t) = 1 гамильтониан

H(t, k (t), c(t), y(t)) = ( f (k (t))− λk (t))e−δt ,

иего максимум по фазовой переменной k(t) достигается при f ′(k (t)) = λ .

Если положить c(t) = f (k (t))− λk (t) , то траектория, соответствующая та-

кому управлению, будет стационарной, так как на ней

dk = −λk(t) + f (k(t))−c(t) = 0 dt

Отсюда следует, что на такой траектории f ′(k (t)) = λ .

Таким образом, при m(t) =1 оптимальное управление определяется как c (t) = f (k (t))−λk (t)

Окончательно получаем:

Поэтому условие f ′(k ) = λ определяет

349

Сформулируем теперь правила оптимального управления эко-

номикой в соответствии с (12.3.7). Пока фондовооруженность меньше k , следует ограничить удельное потребление на минимально допустимом уровне c . Как только фондовооруженность достигнет стационарного зна-

чения k , следует скачком увеличить удельное потребление с c до f (k ) − λk . Если же фондовооруженность больше стационарного значе-

ния, то на потребление следует отправлять весь выпуск: c = f (k ) , и когда за счет проедания фондов экономика выйдет на стационарную траекторию k (t) = k , следует уменьшить удельное потребление до f (k ) − λk .

На стационарной траектории при этом обеспечивается поддержание фондовооруженности и удельного потребления на постоянном уровне: k (t) = k , c(t) = f (k ) − λk .

§ 12.4. МОДЕЛИРОВАНИЕДИНАМИКИ ВЗАИМОДЕЙСТВИЯ РАЗРАБОТЧИКОВ КОММЕРЧЕСКОГО

ИНЕКОММЕРЧЕСКОГОПРОГРАММНОГООБЕСПЕЧЕНИЯ

Вэтом параграфе излагаются результаты анализа смешанной дуополии производителей коммерческого программного обеспечения (для определенности, серверной операционной системы Microsoft Windows) и некоммерческого (для определенности, Linux), полученные автором в 2008 г. путем применения аппарата теории оптимального управления.

Будем предполагать рынок программного обеспечения л и н е й н о

ра с т у щ и м с темпом роста a: в единицу времени на рынок приходят a новых пользователей, т. е. суммарное число пользователей на рынке серверных операционных систем к моменту времени t равно N(t) = N0 + at.

Предположим, что каждый новый пользователь выбирает один и только один продукт: или приобретает лицензионную копию Windows, или бесплатно скачивает копию Linux.

Через nW (t) и nL (t) обозначим суммарное число пользователей, ис-

пользующих на момент t операционные системы Windows и Linux соответственно.

Если обозначить q (t ) д о л ю н о в ы х п о л ь з о в а т е л е й, входящих на рынок в момент t и приобретающих Windows, то доля новых пользователей, приобретающих в этот момент Linux, составит 1 − q(t) , поэтому

350