Семестровая 1 (Методы оптимальных решений) / Методы оптимальных решений учебное пособие

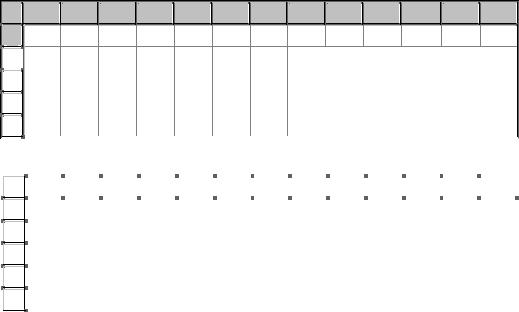
пазон H2:I5, начиная с ячейки H2, содержащей формулу, затем нажать клавишу <F2>, а затем — комбинацию клавиш <Ctrl> + <Shift> + <Enter>. Результат представлен на рис. 2.1.3, б (в ячейках H2:I5). Замечаем, что результаты ручного и компьютерного вычисления произведения матриц совпали. Заметим, что если формула будет введена не как формула массива, то будет рассчитан только левый верхний элемент результата: –3.

б) результаты расчета

Рис. 2.1.1. Вычисление произведения матриц в Microsoft Excel

Нетрудно доказать, что действие умножения матрицы на матрицу обладает с в о й с т в а м и:

(AB)C = A(BC), α(AB) = (αA)B = A(αB),

(A + B)C = AC + BC, A(B + C) = AB + AC, (AB)T = BT AT , AE = EA = A.

Последнее свойство показывает, что единичная матрица E среди всех квадратных матриц данного порядка выполняет такую же роль, как число единица среди чисел. Советуем читателю доказать, что никакая другая матрица в такой роли выступать не может. Указанным обстоятельством мы воспользуемся позже для того, чтобы ввести понятие обратной матрицы.

Произведение матриц, вообще говоря, зависит от п о р я д к а сомножителей: в общем случае

AB ¹ BA .

В отдельных случаях равенство AB = BA может иметь место — тогда матрицы A и B называются перестановочными между собой.

ПРИМЕР 2.1.4. Даны матрицы

41

Решение. Данные матрицы не являются перестановочными, поскольку

42

и AB ¹ BA .

Если A n×n — квадратная матрица n-го порядка, то ее можно умножить саму на себя, и произведение A2 = AA n×n также является квадратной матрицей n-го порядка. Матрицу A2 можно умножить на матрицу A, и тогда получится матрица A3 = A 2 A = AAA n×n того же порядка. Вообще, k-й степенью квадратной матрицы A n×n называется матрица

Ak = AA A n×n .

k раз

По определению считается, что если A ¹ O , то

A 0 = En

(точно так же, как и нулевая степень ненулевого числа равна единице: если a ¹ 0 , то a0 = 1 ).

ПРИМЕР 2.1.6. Вычислить A3 − 2A2 + 2A1 − 4A0 , где матрица A задана в примере 2.1.5.

Решение. Имеем:

В экономике и управлении матрицы очень важны. Рассмотрим одну из типичных задач — задачу планирования производства.

Предприятие может выпускать n видов продукции, используя для этого m видов ресурсов. Известна технологическая матрица

43

затрат ресурсов на производство единицы каждого вида продукции [элемент aij этой матрицы равен количеству ресурса i-го вида (i = 1, 2, …, m), которое необходимо затратить в процессе производства единицы продукции j-го вида (j = 1, 2, …, n)]. Каждый из столбцов технологической матрицы описывает некоторую технологию, т. е. процесс превращения ресурсов в конечный продукт.

Известен также вектор

b1 b = b2

bm

имеющихся в распоряжении предприятия объемов ресурсов и вектор c = (c1 c2 cn )

удельной прибыли предприятия (т. е. cj — это прибыль, которую предприятие получает от реализации единицы продукции j-го вида).

Требуется составить производственную программу, обеспечивающую предприятию наибольшую прибыль с учетом ограниченности запасов ресурсов (вспомним: пример такой задачи мы рассматривали во введении).

Если обозначить через xj план производства продукции j-го вида, то производственная программа предприятия будет задаваться вектором

Суммарный расход первого ресурса на производство всей продукции (всех видов), равный

a11x1 + a12 x2 +…+ a1n xn ,

не может быть больше запаса первого ресурса b1:

a11x1 + a12 x2 +…+ a1n xn b1.

Аналогичные требования должны выполняться и для расходов других ресурсов:

a21x1 + a22 x2 +…+ a2n xn b2 ,

am1x1 + am 2 x2 +…+ amn xn bm .

44

Прибыль предприятия от реализации всей произведенной продукции равна

c1x1 + c2 x2 +…+ cn xn ,

Цель состоит в том, чтобы подобрать отыскать такой план производства (2.1.12), который обеспечит предприятию наибольшую прибыль:

Задачу (2.1.12)—(2.1.14) удобно записать в матричном виде:

z = cx → max,

Ax b,

x θ.

§ 2.2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА

Итак, мы определили вектор как упорядоченную систему чисел и научились складывать векторы и умножать вектор на число. Известно, что аналогичные действия можно выполнять на множестве функций. Для того чтобы с единой точки зрения изучать различные множества объектов, на которых определены операции сложения и умножения на число, вводят понятие линейного пространства.

Множество L элементов

ством, если выполняются следующие условия:

1)имеется правило, которое позволяет построить для каждых двух элементов a и b из L третий элемент из L, называемый суммой элементов a и b и обозначаемый a + b;

2)имеется правило, которое позволяет построить для каждого элемента a из L и любого действительного числа λ элемент a′ из L, называе-

мый произведением элемента a на число λ и обозначаемый λa;

3)существует элемент θ L, называемый нулевым, обладающий свойством (2.1.3), каков бы ни был элемент a; для каждого элемента a из

45

L существует элемент −a L, называемый противоположным и обладающий свойством (2.1.4);

4)правила образования сумм элементов и произведения элементов на число удовлетворяют условиям (2.1.1), (2.1.2) и (2.1.5)—(2.1.9).

Элементы линейного пространства условимся называть векторами

независимо от их конкретной природы.

Множество всех n-мерных векторов — упорядоченных систем действительных чисел — образует линейное пространство в смысле данного определения. Это линейное пространство называется n-мерным арифме-

тическим линейным пространством и обозначается n .

Множество всех матриц одного и того же размера m × n образует линейное пространство, которое обозначается m×n .

В качестве еще одного примера линейного пространства укажем совокупность всех многочленов степени, не превышающей данного натурального числа n, с обычными операциями сложения многочленов и умножения их на числа.

Говорят, что в линейном пространстве L определено скалярное произведение, если имеется правило, которое позволяет каждой паре векторов a и b поставить в соответствие некоторое число, обозначаемое a, b , причем это соответствие обладает свойствами (2.1.11). Линейное

пространство, в котором определено скалярное произведение, называется

евклидовым.

На множестве упорядоченных систем n чисел было определено скалярное произведение по формуле (2.1.10), и мы убедились, что условия (2.1.11) выполнены. Следовательно, арифметическое n-мерное пространство является евклидовым.

Упомянутые ранее линейные пространства матриц и многочленов также можно превратить в евклидовы, если определить подходящим образом скалярное произведение.

Пусть L — линейное пространство, а S L — некоторое подмножество L.

Подмножество S L линейного пространства L называется подпространством этого линейного пространства, если выполняются два условия:

1) для любых двух элементов a, b S сумма этих элементов a + b также принадлежит S;

2)для любого элемента a S и любого числа λ произведением элемента a на число λ λa также принадлежит S.

Очевидно, у любого линейного пространства L существуют два

подпространства, называемых тривиальными: это само пространство L и нулевое подпространство {θ} , состоящее только из нулевого элемента.

ТЕОРЕМА. Если S — подпространство некоторого линейного пространства L, то S само является линейным пространством.

46

Предлагаем читателю самостоятельно доказать эту теорему.

ТЕОРЕМА. Если S1 , S2 — два подпространства некоторого линейного пространства L, то S1 Ç S2 также является подпространством L.

Доказательство. Если a Î S1 Ç S2 и b Î S1 Ç S2 , то это означает, что

a Î S1 , a Î S2 , b Î S1, b Î S2 , поэтому a + b Î S1 , a + b Î S2 и la ÎS1, la ÎS2

для любого числа l Î , а значит, a + b Î S1 Ç S2 и la Î S1 Ç S2 , откуда и следует, что S1 Ç S2 является подпространством L.

Заметим, что объединение двух подпространств в общем случае уже не будет подпространством.

Говорят, что n-мерный вектор b является линейной комбинацией n- мерных векторов a1, a2 , …, ak , если его можно представить как сумму про-

изведений данных векторов на какие-нибудь числа t1, t2 , …, tk Î :

b = t1a1 + t2a2 +…+ tk ak ,

при этом числа t1 , t2 , …, tk называются коэффициентами линейной комби-

нации.

Система n-мерных векторов

называется линейно зависимой, если хотя бы один из этих векторов является линейной комбинацией остальных векторов системы, и линейно независимой в противном случае.

ТЕОРЕМА О ЛИНЕЙНОЙ ЗАВИСИМОСТИ. Система векторов (2.2.1) являет-

ся линейно зависимой тогда и только тогда, когда существуют такие числа l1 , l2 , …, lk , среди которых хотя бы одно отлично от нуля, что имеет место равенство

Доказательство. Необходимость. Пусть система векторов (2.2.1)

линейно зависима, и например, вектор ai является линейной комбинацией остальных векторов:

ai = t1a1 + t2a2 +…+ ti−1ai−1 + ti+iai+1 +…+ tk ak .

Пусть l1 = t1 , l2 = t2 , …, li−1 = ti−1, li = -1, li+1 = ti+1 …, lk = tk , тогда li ¹ 0 , при этом

λ1a1 + λ2a2 +…+ λi−1ai−1 + λiai + λi+iai+1 +…+ λk ak =

= t1a1 + t2a2 +…+ ti−1ai−1 − ai + ti+iai+1 +…+ tk ak = ai − ai = θ,

что доказывает необходимость выполнения условий (2.2.2) для линейной зависимости векторов.

47

или

ai = t1a1 + t2a2 + …+ ti−1ai−1 + ti+iai+1 + …+ tk ak ,

где

t1 = -l1 / l j , t2 = -l2 / l j , …, t j −1 = -l j−1 / l j , t j +1 = -l j +1 / l j , …, tk = -lk / l j ,

что и доказывает достаточность условий (2.2.2) для линейной зависимости векторов.

Теорему о линейной зависимости можно переформулировать так:

система векторов (2.2.1) является линейно независимой тогда и только

ки этой теоремы эквивалентны.

ТЕОРЕМА. Если среди векторов некоторой системы имеется нуль-

вектор, то такая система векторов линейно зависима.

Доказательство. Если среди векторов a1, a2 , …, ak имеется нульвектор, например, ai = θ , то можно положить λi = 1, λ1 = λ2 = …= λi−1 = = λi+1 = …= λk = 0 , и тогда

λ1a1 + λ2a2 + …+ λi−1ai−1 + λiai + λi+iai+1 + …+ λk ak = = 0a1 + 0a2 + …+ 0ai−1 + 1θ + 0ai+1 + …+ 0ak = θ,

значит, система векторов a1, a2 , …, ak является линейно зависимой (по теореме о линейной зависимости).

ТЕОРЕМА. Если некоторая подсистема a1, a2 , …, al системы векторов линейно зависима, то и вся система a1, a2 , …, al , al +1, …, ak линейно за-

висима.

Доказательство. Если подсистема a1, a2 , …, al является линейно зависимой, то

λ1a1 + λ2a2 + …+ λlal = θ ,

где хотя бы одно из чисел λ1, λ2 , …, λl отлично от нуля, значит,

λ1a1 + λ2a2 + …+ λlal + 0al +1 + 0al+2 + …+ 0ak = θ ,

т. е. система векторов a1, a2 , …, al , al +1, …, ak является линейно зависимой (по теореме о линейной зависимости).

Принято называть n-мерные векторы

e1 = (1, 0, 0, …, 0), e2 = (0, 1, 0, …, 0), …, en = (0, 0, 0, …, 1) (2.2.3)

48

единичными векторами n-мерного линейного пространства. Нетрудно видеть, что система единичных векторов n-мерного линейного пространства линейно независима.

ТЕОРЕМА. Любой вектор a = (a1 , a2 ,…, an ) может быть представлен в виде линейной комбинации векторов e1, e2 , …, en :

a = a1e1 + a2e2 +…+ anen .

Доказательство. Действительно,

a= (a1, a2 ,…, an ) = (a1, 0, 0, …, 0) + (0, a2 , 0, …, 0) +…+ (0, 0, 0, …, an ) =

=a1 (1, 0, 0, …, 0) + a2 (0, 1, 0, …, 0) +…+ an (0, 0, 0, …, 1) = a1e1 + a2e2 +…+ anen ,

что и доказывает теорему. Приведем без доказательства еще три теоремы о линейной зависи-

мости векторов.

ТЕОРЕМА. Пусть n-мерные векторы b1, b2 , …, bm линейно выражаются через векторы a1 , a2 , …, ak . Если m > k, т. е. число линейных комбинаций больше числа данных векторов, то векторы b1, b2 , …, bm линейно зависимы.

ТЕОРЕМА. Если векторы двух конечных систем линейно независимых векторов линейно выражаются друг через друга, то эти системы имеют одинаковое число векторов.

ТЕОРЕМА. Если в системе n-мерных векторов число векторов m больше размерности векторов, т. е. m > n , то такая система векторов

линейно зависима.

Пусть дана система n-мерных векторов .a1, a2 , …, am . и из нее выделена некоторая подсистема векторов ai1 , ai2 , …, air . Условимся называть эту

подсистему базисом данной системы векторов, если векторы подсистемы линейно независимы, а любой вектор исходной системы является линейной комбинацией векторов подсистемы.

Очевидно, что если добавить к базису . ai1 , ai2 , …, air системы векторов a1, a2 , …, am произвольный вектор a j этой системы, то система ai1 , ai2 , …, air , a j будет линейно зависима.

ТЕОРЕМА. Любые два базиса одной и той же системы содержат

одинаковое число векторов.

Эта теорема позволяет ввести новое понятие. Число векторов в произвольном базисе системы векторов называется рангом системы векторов.

До сих пор мы применяли понятия базиса и ранга к системе, состоящей из конечного числа векторов. Теперь распространим эти понятия на системы с бесконечным числом векторов, так как согласно этой теореме базис любой такой системы состоит из конечного числа векторов, не превосходящего их размерности.

49

В частности, можно говорить о базисе и ранге всех n-мерных векторов, т. е. n-мерного линейного пространства. Одним из базисов этого линейного пространства является единичный базис — система единичных векторов e1, e2 , …, en . Так как число векторов в этой системе равно n, то любой базис n-

мерного линейного пространства должен содержать ровно n векторов. Поэто-

му часто говорят: набор любых n линейно независимых векторов n-мерного линейного пространства называется базисом этого линейного пространства.

ТЕОРЕМА. Всякий вектор n-мерного линейного пространства можно, и притом единственным образом, разложить по векторам базиса этого линейного пространства.

Доказательство. Пусть a1 , a2 , …, an — какой-нибудь базис, а x —

произвольный вектор n-мерного линейного пространства. Система n + 1

векторов a1, a2 , …, an , x линейно зависима, т. е. l1a1 + l2a2 + + lnan + +ln+1x = θ , где ln+1 ¹ 0 (в противном случае векторы a1 , a2 , …, an были бы

линейно зависимы). Если положить xi = -li / ln+1 , то можно выразить x через a1 , a2 , …, an следующим образом:

x = x1a1 + x2a2 + + xnan ,

что и доказывает теорему.

Коэффициенты x1 , x2 , …, xn разложения вектора x по векторам базиса a1 , a2 , …, an называются координатами вектора x в данном базисе. В силу

единственности линейного выражения вектора через линейно независимые векторы, как было доказано ранее, координаты вектора в данном базисе определяются однозначно. Координаты вектора, определенные при введении понятия вектора, — это коэффициенты разложения данного вектора по единичному базису.

Пусть дана прямоугольная матрица

произвольной матрицы A равен рангу системы ее столбцов

50