§ 29. Интегральный оператор канонического преобразования.

Можно решать задачу в разных представлениях. Преобразование, осуществляющее замену переменных, в которых рассматривается задача, называется каноническим преобразованием.

Запишем:

(*)

(**)

Сравним эти равенства с

Тогда можно рассматривать как ядро некоторого интегрального преобразования, переводящего- представление в-представление.

Обозначим

,

где

Собственная функция оператора в-представлении играет роль ядра интегрального оператора, осуществляющего преобразование отк.

Аналогично

Из соотношения (*) следует, что для того чтобы говорить о функции надо знать коэффициенты разложения. Т. е. знаяможем записать:

Чтобы знать коэффициенты надо знать- это следует из (**)

Тогда задать состояние мы можем либо функцией , либо функцией. Эту информацию мы задаем в разложении переменных.

Оператор осуществляет переход отпеременных кпеременным:

.

Это есть каноническое преобразование переменных.

Установим связь между и:

,

,

подставим одно в другое

,

тогда

(***)

Д.З. записать это равенство на языке ядер.

Распишем:

также

Этому соответствует соотношение операторов

Из (***) следует , тогда

,

отсюда

получили, что оператор унитарный.

Рассмотрим норму функции и обнаружим унитарность:

{используем равенство Парсеваля},

тогда ,.

Равенство Парсеваля:

.

Мы знаем, что ядро оператора

,

есть собственная функция оператора в- представлении.

Тогда ядро оператора :

,

есть собственная функция оператора в-представлении.

Но

.

Задачи Штурма-Лиувилля имеют вид:

,

.

-собственная функция оператора в -представлении есть комплексносопряженная собственная функция оператора в- представлении.

Отсюда запишем:

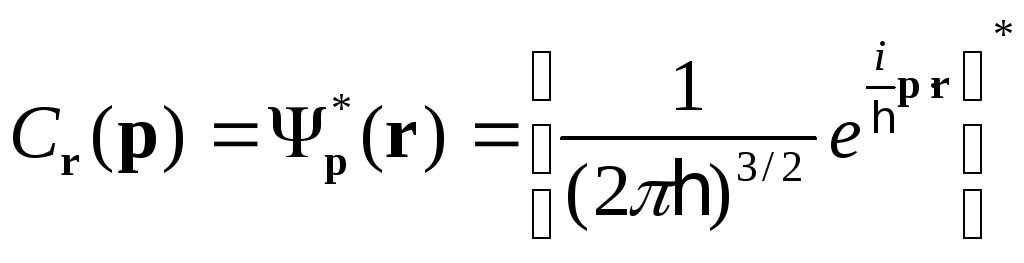
§ 30. Каноническое преобразование оператора.

Рассмотрим произвольный оператор в- представлении

. (1)

В -представлении

(2)

Воспользуемся

,

,

тогда

.

Но и

.

Из (1) получим

{из (2)}.

Получили равенство

, (3)

связь между операторами в разных представлениях.

Из (3) получим модификации (исп. Унитарность ):

,

.

Или в интегральной форме

(*)

={подставим соотношения ,}

Далее

и .

Также

, (**)

здесь .

.

И

,

.

§ 31. Уравнения Шредингера в матричной форме.

(1)

(2)

Стационарное и нестационарное уравнения Шредингера.

Перейдем к матричной форме. Привлечем оператор .

(3)

Пусть волновые функции подчиняются ортонормированности:

(4)

Тогда можно разложить по собственным функциям оператора :

(5)

Подставляем (5) в (1) и получаем

Умножим это выражение на и проинтегрируем по объему, тогда получаем уравнение Шредингера в матричной форме

,

где

.

Матричный элемент перехода из n в m.

Пример. В случае когда собственными функциями в разложении являются функции оператора Гамильтона, т.е.

.

Тогда уравнение Шредингера

.

Интегрируя, получим

.

§ 32. Линейный гармонический осциллятор

В классической механике функция Гамильтона линейного гармонического осциллятора:

.

Рассмотрим задачу в - представлении.

Используем принцип соответствия классической и квантовой механик, тогда

(1)

Используем квантовой уравнение Ньютона:

(2)

Подставим (2) в (1) , получим

(3)

Осуществим переход к матричной форме. Пусть

, (4)

где

Подставии (4) в (3)

.

В квантовом линейном осцилляторе возможны переходы между двумя ближайшими уровнями, тогда

.

Здесь матричные элементы .

Остальные переходы запрещены, тогда матричные элементы .

Спектр энергии квантового гармонического осциллятора

.

Таким образом энергетический спектр начинается не с 0, а с энергии нулевых колебаний (при )

§. 33. Проблема трех Н.