§98 Энергетическое представление в случае дискретного спектра: волновая функция, оператор и их свойства.

Напомним некоторые результаты из теории представлений.

Рассмотрим волновую функцию =и разложим эту функцию в интеграл по собственным функциям оператора

= ; - ЗШП для

где - эти функции удовлетворяют условию нормировки:

, =

Перепишем интеграл :

= =

т.е. собственную функцию оператора впредставлении обозначили:

тогда получаем:

= { некоторое интегральное соотношение, которое

можно записать как действие оператора на

функцию в других переменных } =

Это некоторое каноническое преобразование, которое осуществляется с помощью оператора с ядром.

Имеем преобразование вида

Переменные и указаны в ядре оператора и оператор – унитарный, он не нарушает правила нормировки.

Определение унитарного оператора : .

Существует обратное преобразование:

Функция – это функция в– представлении

Как коэффициент разложения в интеграл, она получается :

И дальше будем писать , чтобы подчеркнуть, что– это не столько коэффициент разложения, сколько функция, а – это её аргумент.

Как всё это скажется на произвольном операторе?

- это оператор , действующий в представлении

- получили новую функцию в тех же переменных.

Запишем это в форме ядра:

C другой стороны, можем разложить по базисным функциям, которые использовали вначале:

Коэффициенты разложения определяются: , подставим сюда

, тогда:

т.е. , где

Используя, что и ещё

вводится обозначение: , тогда

Тогда получим:

здесь всё в здесь функция в координатном пред-

q - представлении ставлении, а ядро оператора и интег-

рирование идёт по переменным

другого представления.

Посмотрим, как оператор действует в –представлении.

Во-первых:, это в операторной форме,

перепишем это равенство в ядерной форме:

интегрирование идёт по

= тем переменным, которых

нет в левой части равенства

т.к., то ядро

т.к., то ядро

Легко показать, что ядро

это есть результат действия это всё функция от

оператора на функцию

Запишем результат действия оператора на некоторую функцию в- представлении:

,

но ,тогда мы получили ( 1 )

Араньше мы получали ( 2 )

Здесь стоят матричные элементы вида ,

но у них различный порядок следования и_: и.

Распространим наше рассмотрение на дискретный спектр:

Пусть – оператор с единичным спектром.

Здесь условие нормировки не на - функцию, а на единичный тензор:.

Во всех полученных выше формулах заменяем: _.

И обозначаем: Скалярное произведение .

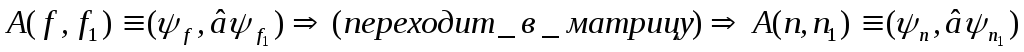Часто пишут с тем, чтобы показать, что это матричный элемент.

-это матрица с бесконечным числом строк и столбцов.

Имеем: ( 3 )

по аналогии с ( 1 )

( 4 )

по аналогии с ( 2 )

Перенесём всё полученное выше на энергетическое представление:

Рассмотрим оператор , который обладает дискретным спектром, т.е. , таким образом, переходим от представления к - представлению(или энергетическому представлению).

Условие нормировки:–это условие квадратичной интегрируемости– функций.

Коэффициенты разложения , где – это волновая функция в

энергетическом представлении.

Ядро любого оператора в энергетическом представлении переходит в матричный элемент:

, где

- это конкретные собственные функции оператора .

Найдём матричный элемент оператора в энергетическом представлении:

{используем решение ЗШП:} =

, где

- это собственное значение оператора из ЗШП.

Матрица оператора диагональна в энергетическом представлении.

Соотношения ( 3 ) и ( 4 ) переносятся в представление без изменений.