§ 106 Оператор в -представлении.
Действие оператора
на функцию 
,
в 
-
и 
-представлениях.
Запишем формулы:
,
оператор 
действуя на 
переводит ее в функцию 
.
Функцию 
можно разложить по базису функций 
:
(*)-- суммирование по числам заполнения
одночастичных состояний.
Коэффициенты
разложения представляют собой матричные
элементы: 
- числа заполнения
в одночастичном состоянии.
Это было в 
- представлении.
Посмотрим действие
в 
-представлении.
Разложим по базису:
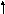
эта матрица есть
оператор 
в 
-представлении.
Разложение функции
по одночастичным состояниям 
.
- описывает весь
ансамбль частиц
- функция одночастичного
состояния.
Напомним, что
и 
.
Для одночастичной
функции писали уравнение: 
,
функции 
- образуют базис, по ним можно разложить
функцию одной переменной. Но функция
N-переменных. Размножим ее по базису в
интеграл: 
- вообще эти коэффициенты есть функция
оставшихся от 
аргументов, а именно - это есть матричные
элементы:
(1) – интегрирование
и суммирование по одной переменной 
(интегрирование по 
и суммирование по 
),
при интегрировании и суммировании i-тая
координата 
выходит. Приведем интеграл (1 стр. 23б) к
более простому виду, для этого вспомним,
что: 
(2)
Оператор
перестановки
Вспомним условие
нормировки дл одночастичных функций:
;
i – индекс указывает переменную, по которой идет интегрирование.
В формуле (2) имеется
одна функция 
т.е. из 
надо
выделить функцию 
,
которая соответствует 
из (1 стр 23б лекции: 
).
Модифицируем 
:
В сумму условия
нормировки, беря интеграл (1 стр 23 б
лекции: 
)
получим множитель 
,
и еще останется некоторая функция от
оставшихся от интегрирования переменных,
а именно:
эта часть содержит N-1
частицу, уже просматривается
волновая функция,
описывающая N-1 частицу.
Обозначение: 
- означает, что здесь не хватает 1-частицы
в a-том состоянии,
а именно:
, тогда как было 
тогда имеем, положив
,
чтобы
,
Запись 
означает, что в наборе 
нет переменной 
,
т.к. она стоит после “;”.
Запишем 
с учетом полученного:
- суммирование по
всем одночастичным состояниям, состояния
от индекса i не зависят , поэтому ai
писать нехорошо, и i
убирают к функции.
Матричный элемент одночастичного оператора:
,
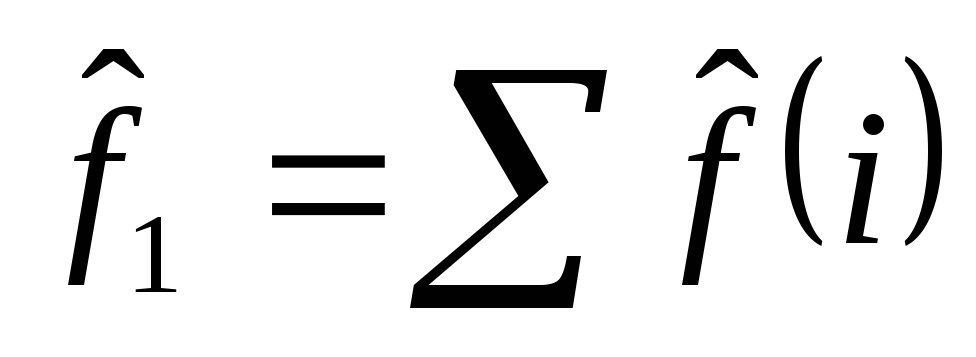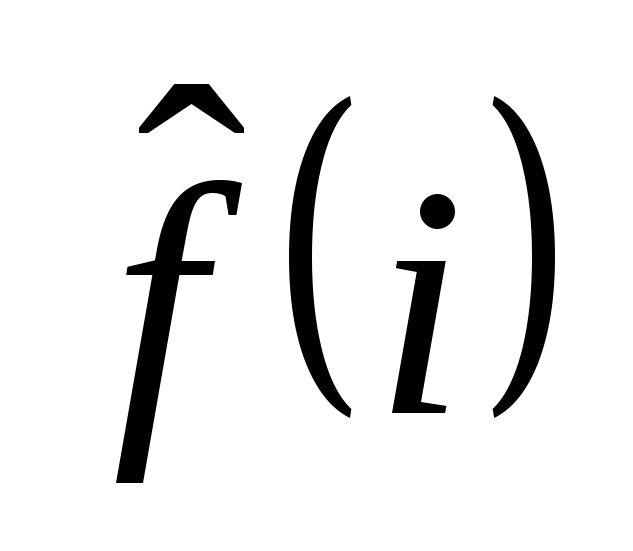- оператор действующий на переменные
i-той частицы: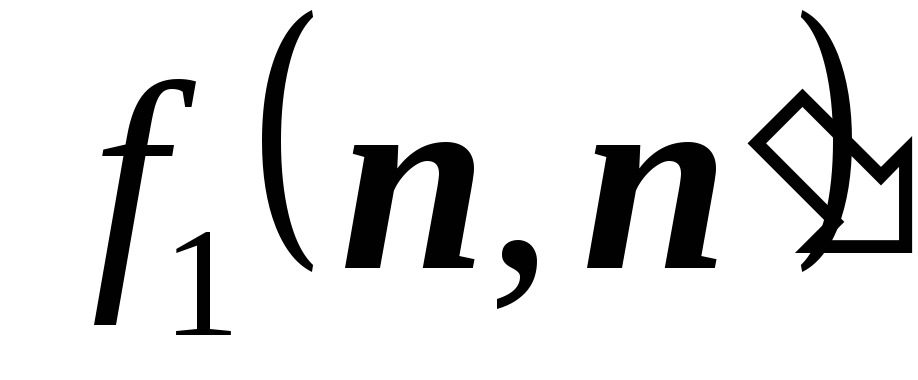 
.
Запишем этот матричный элемент в форме скалярного произведения:
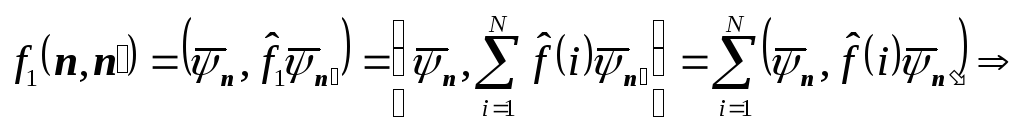
т.к. функции 
симметричны по перестановке частиц, а
оператор 
не зависит от i-той частицы, то получаем
умножение на число частиц N и берем любую
i из N
сюда надо поставить 
в виде (2 )
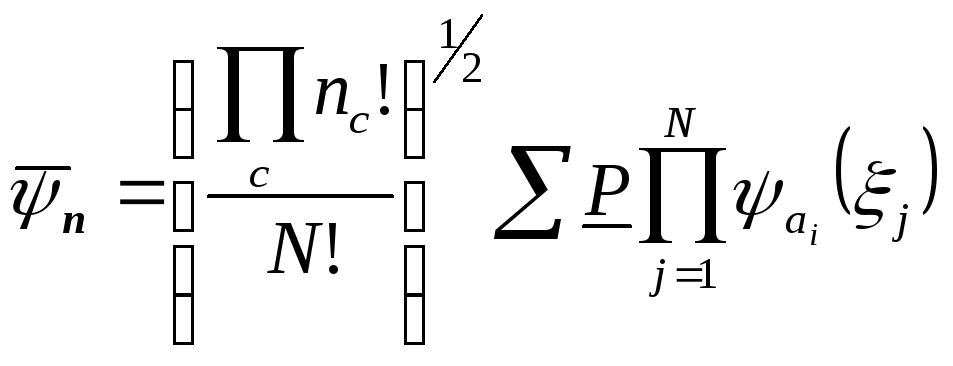
произойдет разделение переменных, i-тая переменная выделится, а остальные переменные останутся вместе.
Пусть (3)
(4)
a и b – это наборы одночастичных состояний (5)
и
- это наборы чисел заполнения.
Сократить
Оставшееся
интегрирование есть скалярное
произведение: 
- здесь у функций убрали индекс (i),
т.к. в скалярном произведении стоят
симметричные функции, и индекс (i) можно
не указывать. Тогда, запишем матричный
элемент: 
.
Мы имели условие ортонормы.
________
,
чтобы это скалярное произведение было
не ноль, требуется чтобы соответствующие
числа заполнения совпадали:
т.е. нужно, чтобы: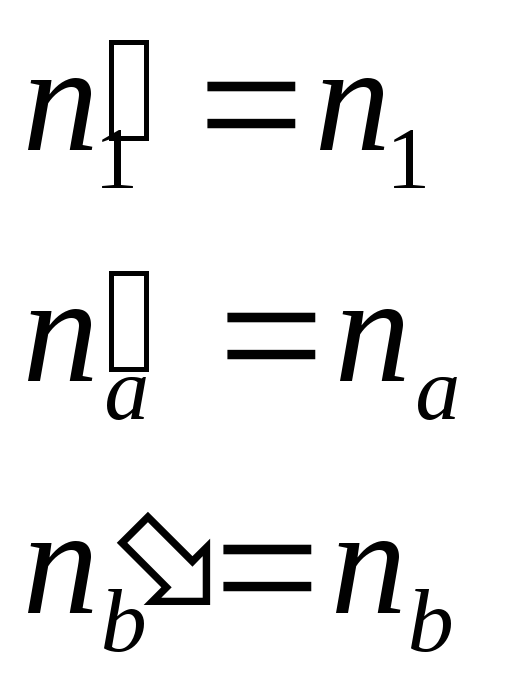
Тогда 
В этом случае имеем для чисел заполнения:
введем число nc,
когда c≠a,b,
для этого числа имеется равенство
а для состоянийa
и b
имеются равенства:
тогда
имеем матричный элемент 
в
виде: 
Матричные элементы
Рассмотрим матричный элемент такого вида:
(6)
Теперь рассмотрим матричный элемент, транспонированный:
(7)
Теперь рассмотрим матричный элемент комплексно сопряженный и транспонированный и с индексом a:
В (7) 
в силу вещественности этих матричных
элементов.
Тогда имеем 
Можем упростить
выражение для 
(см стр. 26 б 
),
для этого вспомним произведение матриц:
,
т.е.
Тогда имеем 
,
т.е. мы имеем:
