
- •§98 Энергетическое представление в случае дискретного спектра: волновая функция, оператор и их свойства.
- •§99Энергетическое представление в случае дискретного спектра: методы Шредингера и Гейзенберга.
- •, ( 1 )
- •§102Операторы рождения и уничтожения
- •§103 Свойства рождения и уничтожения. Оператор .
- •§104 Полином Эрмита (пэ) и функции Эрмита (фэ).
- •Метод вторичного квантования в случае статистики Бозе-Эйнштейна (б-э).
- •§ 105 Волновая функция в - представлении:
- •§ 106 Оператор в -представлении.
- •§107 Операторы рождения и уничтожения частиц.
- •§108 Оператор в- представлении.
- •- Одночастичных состояний.
- •§109 Оператор Гамильтона в методе вторичного квантования.
- •§110 Операторы вида и их свойства.
- •Метод вторичного квантования в случае статистики Ферми-Дирака(ф-д). Основные формулы.
- •Предмет и метод статистической физики. Статистическое описание систем с большим числом степей свободы.
- •§111 Системы с большим числом степеней свободы.
- •§112 Метод статистической физики (Элементы теории вероятностей).
- •§113 Микро- и макро- параметры систем.
- •§114 Свойство эргодичности системы.
- •§115 Два способа усреднения в стат физике.
- •§116 Понятие ансамбля систем.
- •§117 Эргодическая гипотеза.
- •§118 Равновесное состояние у системы.
- •§119 Время релаксации.
- •§120 Квазизамкнутость с статическая независимость подсистем.
- •§121 Принцип равновероятности микросостояний.
- •§122 Статистический вес макросостояния.
- •§123 Статистическая энтропия.
- •§124 Теорема Лиувилля.
- •§125 Микроканоническое распределение Гиббса. Рассмотрим замкнутую систему, и согласно принципу равной вероятности, все состояния системы, с заданной энергией , равновероятны.
- •§126 Каноническое распределение Гиббса.
- •§127 Принцип возрастания энтропии.
- •Добавление к т. Лиувилля
- •Добавление к микроканоническому распределению Гиббса.
- •§128 Каноническое распределение Гиббса.
- •§129 Флуктуации аддитивных величин. Рассмотрим величины, которые для всей системы связаны с аналогичными величинами подсистем по закону суперпозиции: ,
- •Посмотрим среднее от аддитивной наблюдаемой случайной величины:
- •§§ Энтропия и статистический вес.
- •§130 Температура.
- •§131 Статистическая сумма и ее свойства.
- •§132 Функция распределения вероятностей по энергии w(e) и распределение Гаусса.
- •§133 Квазиклассическое приближение в статистической физике.
- •- Это площадка, описывающая состояние
§113 Микро- и макро- параметры систем.
В связи с тем, что системы обладают большим числом степеней свободы, и с тем что мы перешли на язык теории вероятностей, мы рассмотрим этот вопрос.
Каждое состояние
системы описывается набором динамических
переменных
![]() и
и![]() .
.
В ансамблях таких
систем, из большого числа параметров,
которые можно построить на 2n
– переменных
![]() и
и![]() ,
можно выделить небольшое число параметров,
которые важны для описания системы.
Введём такой некоторый параметр:
,
можно выделить небольшое число параметров,
которые важны для описания системы.
Введём такой некоторый параметр:
![]() .
.
Выясняется, что эта величина в зависимости от t может принимать различные значения, т.е. является функцией от t. Она является микропараметром системы, т.к. он определяет систему на её части, на подсистеме. Наряду с системой можно рассмотреть подсистему. Наряду с этой величиной вводится параметр аналогичный, который определяется в более продолжительный момент времени и характеризующие систему в целом – макропараметр.
Стационарность. Будем рассматривать в этом курсе стационарные явления или стационарные системы свойства которых не меняются во времени, т.е. не зависят от времени. Т.е. если рассматривать ось t, то для стационарных сред начало наблюдения за системой можно выбрать в любой точке оси t:

t
![]()
![]()
И для таких процессов начальные условия динамических переменных не оказывают влияние на результат, т.е. начальные условия могут быть отброшены, т.к. часы пускаем в любой момент времени.
Итак в стационарных системах:
время начала отсчёта
 можно перемещать по оси времени;
можно перемещать по оси времени;начальные условия, оказывается, не влияют;
граничные условия, оказывается, не влияют на систему, если система стационарна.

Через граничные условия внешнее воздействие проникает . И через некоторое время действует
на систему, действие идёт через точки, находящиеся в очень узком приграничном слое. Т.к. этих мало по сравнению с точками системы, то граничные условия можно не учитывать.
Э то
обстоятельство можно использовать при
рассмотрении двух подсистем. Взаимодействие
подсистем в достаточно малом промежутке
времени не оказывает влияние на
подсистемы, т.к. точек на границе
то
обстоятельство можно использовать при
рассмотрении двух подсистем. Взаимодействие
подсистем в достаточно малом промежутке
времени не оказывает влияние на
подсистемы, т.к. точек на границе![]() пренебрежимо мало по сравнению с самими
подсистемами. Выясняется, что микро-
и макро- параметры А, если наблюдать за
ними в течении большого промежутка
времени, то в течении длительного
пренебрежимо мало по сравнению с самими
подсистемами. Выясняется, что микро-
и макро- параметры А, если наблюдать за
ними в течении большого промежутка
времени, то в течении длительного
большей части этого промежутка времени, система обладает конкретными или близкими к нему параметрами. Если усреднить этот параметр по времени, то он не будет отличаться от конкретного параметра;
в качестве результата наблюдения А, принимается значение <среднее по времени А>
A = {A} =
![]()
Е![]() сли
Т – время наблюдения, то это правильно,
сли
Т – время наблюдения, то это правильно,
Но Т – очень велико, поэтому пишут предел
Это предлагают воспринимать как наблюдаемую величину (в теории).
§114 Свойство эргодичности системы.
Понятие эргодичности.
Итак мы рассмотрели такие функции:
A = A[![]() ,
,![]() ]
]
Параметр А испытывает флукткации, отклонения от некоторого среднего значения, в течении времени. Наряду с зависимостью А от t можно ввести характеристику вероятность того, что А лежит в интервале А ~ A+dA:
dW(A) = ω(A)da
Как получить эту вероятность? Очевидно, если у нас стоит: (1) А=<A(t) < A+da, то мы можем подсчитать все промежутки времени их сумму Σdti , в течении которых Аi(ti) попадает в интервал (1): например ti < ti < ti+dti . Т.е. мы подсчитаем длительность пребывания А в слое А ~ A+dA
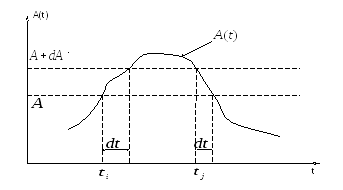

Оказывается, если dt одинаковые, то Σdti ~ dt
Но оказывается еще: Σdt I ~ T, где Т – время наблюдения.
Тогда dW =![]() Σdti
(2)
Σdti
(2)
Зная эту величину
мы можем найти значение любой функции
времени, любой наблюдаемой величины.
Т.е. мы нашли плотность вероятности ω(t)
= dW/dt
; t
– это не случайная величина, а параметр;
а случайной величиной является A(t).
С помощью функции (2) можно найти среднее
по времени значение для наблюдамой
величины: {A} =
![]() (это
определение среднего по времени)
(это
определение среднего по времени)
Мы писали
dW =![]() Σdti
– это вероятность того, что случайная
величина A(t)
лежит в пределах А=<A(t)
< A+da.
Таким способом можно рассматривать 2
способа усреднения.
Σdti
– это вероятность того, что случайная
величина A(t)
лежит в пределах А=<A(t)
< A+da.
Таким способом можно рассматривать 2
способа усреднения.
