§130 Температура.

а) Статистич. определение.

Мы ввели определение температуры, исп. 1 начало термодинамики: ,

т. е. (1) , причем это в равновесном состоянии

Хотя а не только,так тоже можно брать. Но мы брали.

Температура выражена (1), через энтропию, а энтропия это стат. параметр, поэтому температура это тоже статистич. параметр.

§ б) Условия равновесия систем находящихся в тепловом контакте.

Запишем энтропию для системы 1+2 термостат, где вся система- замкнутая

Можно записать

Рассмотрим случай когда система выведена из состояния равновесия. Система будет переходить в равновесное состояние и энтропия системы должна возрастать при этом переходе: , тогда

и зависит от, через. Мы полагаем только тепловой, или энергетический контакт.

(равновесие системы может

наступить через приход в

равновесие отдельных подсистем)

т. к. система целиком замкнута, то , то и, тогдат.е.

тогда

тогда процесс установления равновесия

описывается таким неравенством.

Отсюда имеем, что видно, что еслитоИдет перекачка энергии от 2 к 1 системе, т. е.

идет повышение температуры в 1.

Когда достигает максимума, т. е. имеем установление равновесия, то имеем- это условие равновесия 1 и 2 подсистем.

§131 Статистическая сумма и ее свойства.

Мы определили каноническое распределение: ,

и

сумма по состояниям, а не

по энергетическим уровням.

И энтропия (1)

Найдем:

(2)

это

константа

Тогда, учитывая язык термодинамики ,

Введем свободную энергию Гельмгольца

Тогда (*)

Тогда имеем, что я определяется через :

тогда можем записать:

Мы будем часто использовать

здесь - в энергетических единицах.

Используем определение я для нахождения . Запишем определение среднего:

{здесь можно найти сумму

=используя дифференцирование по параметру}

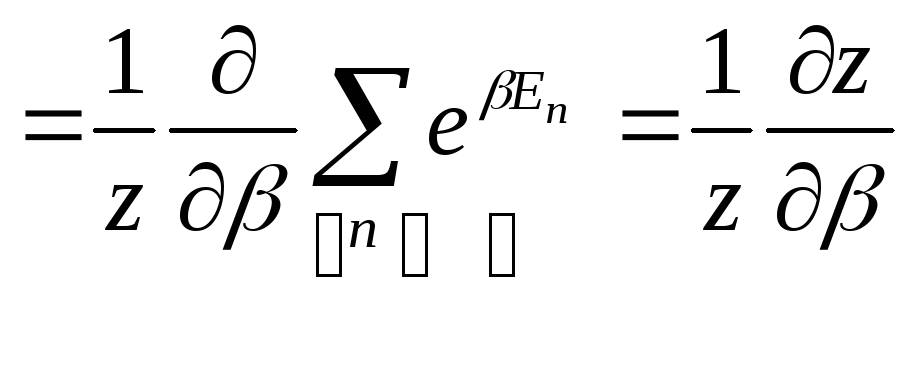
=def z

тогда {используя(*)}

А в духе термодинамики , тогда

- соотношение между энергией и свободной

энергией .

Д/з2 Роль числа степеней свободы с стат. физике (где с увеличением степеней свободы идет переход кол-ва в качество, и что имеет место с уменьшением числа степеней свободы).

Д/з3 Связь между и еще их связь с.

Д/з4 Рассчитать 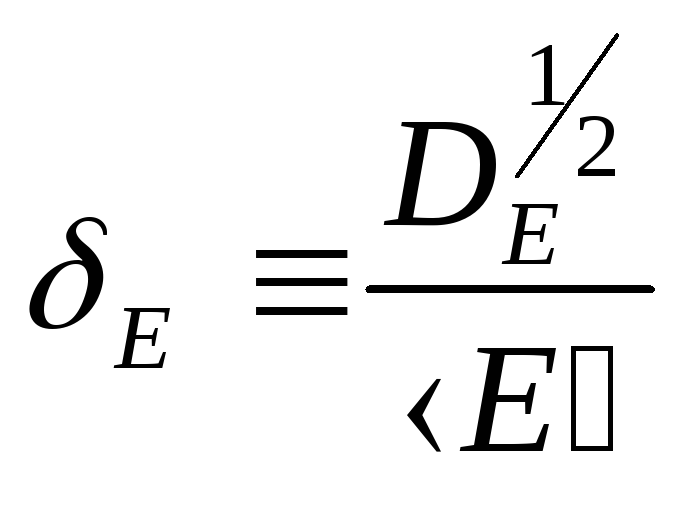приn=2, т. е. .

Мы получили связь между энергией и стат. суммой

Где ,

Найдем связь

это по определению

среднего

Найдем :

def

{подставим }

суммирование по

состояниям

={исп. дифференцирование по параметру :

}=

тогда

Раньше получили

тогда(*)

покажем это

.

Компактное выражение (*) можно связать с

Тогда установим связь:

Раньше получили, что

где

Тогда

Теперь, если пишем это для термодинамических величин, то и

def

ивеличина- это теплоемкость при постоянном объеме (в

термодинамике). Это теплоемкость

говорит о том, что всей системы

объем постоянен

тогда, здесь-безразмерная, а- в энергетич. единицах

это линейная

апроксимация

удельная теплоемкость- это теплоемкость в расчете на единицу массы.

- теплоемкость в расчете на 1-ну частицу.

тогда

отсюда следует положительность

теплоемкости ,