Метод вторичного квантования в случае статистики Бозе-Эйнштейна (б-э).

§ 105 Волновая функция в - представлении:

1. Оператор k-частичных взаимодействий

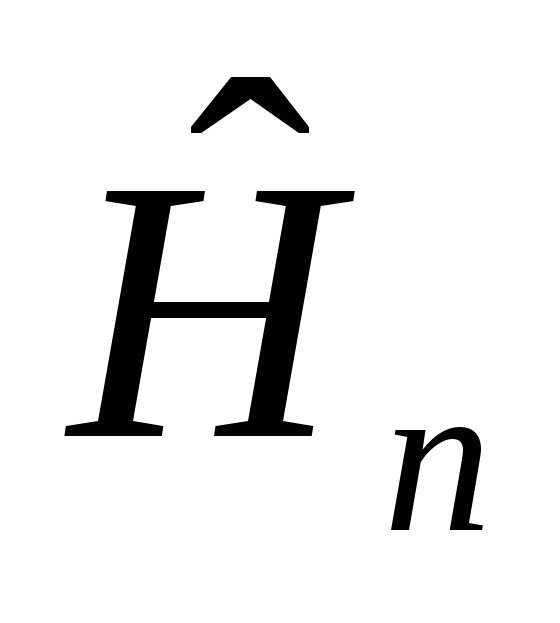
Для решения квантовой механики надо записывать оператор , будем решать стационарную задачу, т.е. время выбросим из рассмотрения.

Оказывается можно представить в случае системы частиц в виде суммы: , где - описывает k-частичные взаимодействия.

Рассмотрим оператор - описывает одночастичное взаимодействие: . описывает систему из N частиц, невзаимодействующих между собой (свободных частиц), но эти частицы могут взаимодействовать с внешними полями.

Индекс i – это координата i-той частицы.

Под i понимаем: , где - спиновая переменная ( – квантовое число).

Ансамбль Бозе-частиц – это частицы с целым спином. Здесь принцип Паули

не действует, в любом состоянии может находиться любое число частиц.

Можно записать: (*)

- отвечает за взаимодействия между частицами

- не учитывает взаимодействие между частицами.

Часто (*) можно решать как в теории возмущений, т.е. .

Посмотрим - оператор для одной частицы. Например, без учета спина оператор кинетической энергии имеет вид: 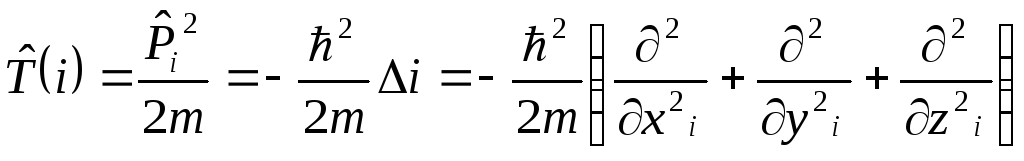- здесь без учета спина.

m без индекса – m_i, т.к. у нас все частицы одинаковые – это бозоны.

2. З Ш-Л для оператора

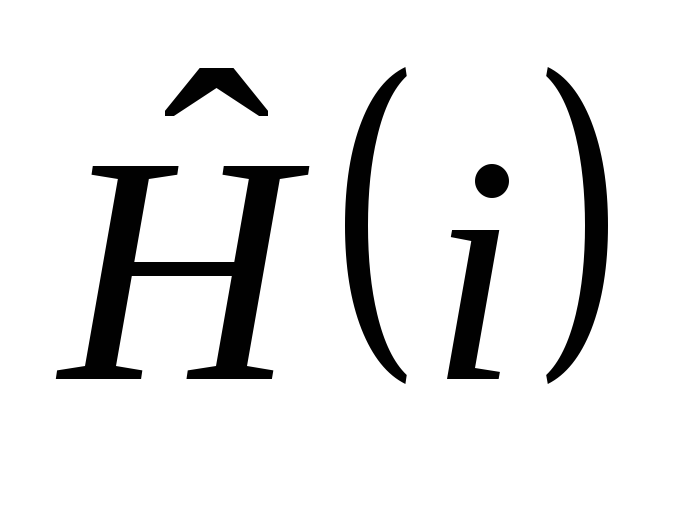
Заменим З Ш-Л следующим образом: - для i-той частицы.

Индекс a_i – набор квантовых чисел (всевозможные значения квантовых чисел, характеризующих одночастичное состояние – это a, тогда a_ia=1,2,3,.. – можно одночастичные состояния пронумеровать числами).

i = 1,…,N, для всех i З Ш-Л имеет один и тот же вид, индекс i можно не писать.

Условие нормировки: - это для

одночастичных состояний. a и b – одночастичные квантовые числа.

- функция - представляет собой базис, по которому можно разложить произвольную функцию переменной . - собственная функция оператора .

суммирование по всем одночастичным состояниям

3. З Ш-Л для оператора

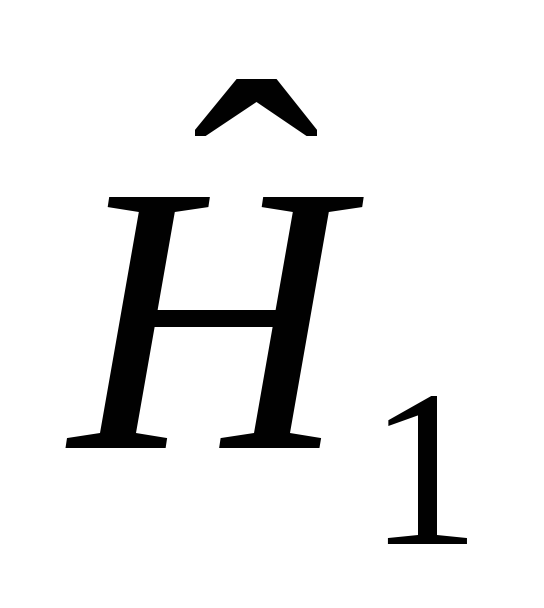
- это оператор одночастичного взаимодействия

Запишем соотношение:

, т.е. и - коммутативны, т.к.

при i=j - т.к. оператор коммутативен сам себе.

при i≠j - т.к. операторы действуют на различные переменные.

Запишем З Ш-Л в виде: - набор квантовых чисел, относящихся к каждой частице, т.е. набор всех одночастичных координат.

Вследствие того, что одночастичные операторы коммутативны, то срабатывает метод разделения переменных и тогда ~ - произведение всех одночастичных функций.

Учтем принцип тождественности, т.е. симметризацию по перестановкам для

Бозе-частиц, тогда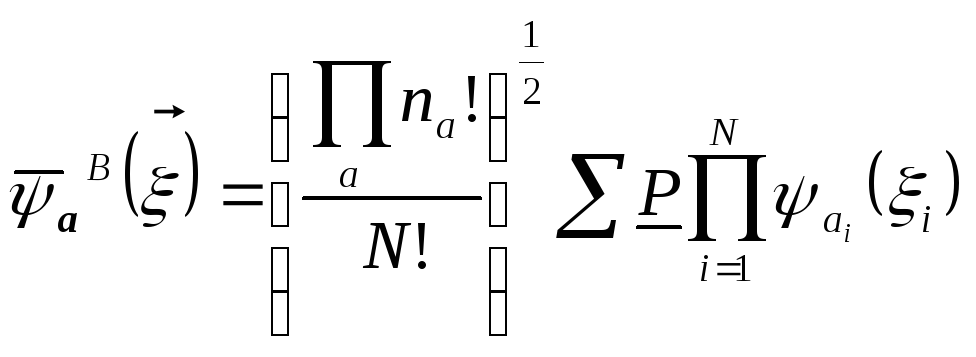

Сортировка частиц - сумма по всем нетождественным

Бозе-частиц. перестановкам

Оператор перестановок - действует на координаты .Функции являются собственными функциями Эрмитового оператора, они квадратично интегрируемы, вводим их нормировку:

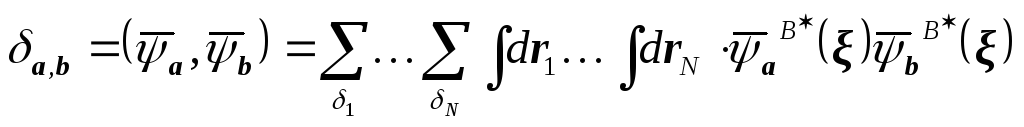
N-сумм N-интегралов

В случае получают нормированную константу.

Посмотрим, что такое n_a. Если в каком либо из состояний ”a” нет частиц, то n_a!=0!=1. Если n_a≥0, то появляется факториал, отличный от 1.

Множитель появляется, т.к. точки не обязательно различны между собой, хотя точки могут находится в разных частях ансамбля.

Например при N=4 может оказаться: ,,, тогда число частиц а 1-ом кв. состоянии n₁=2, число во 2-ом кв. состоянии n₂=1, n₃=n₄=0, n₅=1.

Числа n_a – числа заполнения одночастичных состояний.

- суммирование по всем одночастичным состояниям чисел заполнения дает число частиц N в системе. Если совершаем перестановки, то в (*) выкладываем тождественные перестановки, т.е. перестановки частиц, находящихся в одном и том же квантовом состоянии.

Функции - составляют базис по которому можно разложить произвольную функцию переменных : 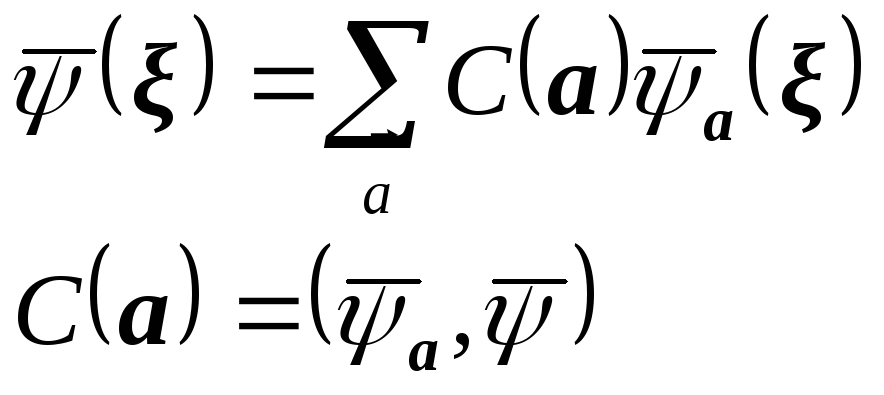Здесь индекс «B» опустим.

- указывает на состояние системы из N независимо действующих частиц.

4. -представление (метод вторичного инвертирования)

Мы ввели функцию, которая описывает ансамбль не взаимодействующих

бозонов:.Индекс - набор одночастичных квантовых чисел. Часто бывает удобнее вместо индекса описывать заполнение одночастичных состояний при помощи набора чисел заполнения одночастичных квантовых состояний , т.е. , - набор чисел заполнения.

Рассмотрим наш пример при N=4

Здесь (1,1,2,5),

Тогда (2,1,0,0,1,0,0,…) – бесконечный ряд, набор чисел заполнения.

Функции - ортонормированны и образуют базис. Условие ортонормированности: - произведение по всем одночастичным состояниям.

1-получается, когда числа заполнения всех одночастичных состояний будут одинаковы слева и справа.

Функции образуют базис:.

Коэффициенты играют роль волновой функции в представлении чисел заполнения, т.е. в -представлении.

Для энергии, которая описывает состояние N частиц:через числа заполнения- суммирование по всем заполненным состояниям.

Эта сумма короче, чем эта.

Л: Тябликов С. В. «Методы квантовой теории магнетизма», 1975