Квантовая механика

§ 1. Экспериментальные основы квантовой механики

1900 г. Планк ввел понятие о квантах и ввел квантовую постоянную. Работа Планка объясняла теорию излучения твердых тел.

1905 г. Классификация спектров Ритцем и Ридбергом. Все спектральные линии могут быть посчитаны через термины , где- постоянная Ридберга,n – натуральное число.

1913 г. Н. Бор теоретически объяснил спектр атома водорода (постулаты Бора).

Эксперименты Франка и Герца. Они рассматривали неупругое рассеяние электронов на атомах. Пропускали пучки электронов через пары ртути. При определенных энергиях, электроны при соударении с атомами ртути теряли часть своей энергии.

Рис.1. Упругое соударение.

Рис. 2. Неупругое соударение

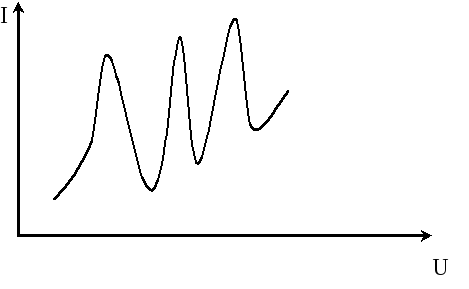
Рис. 3. Зависимость тока I от напряжения U (ВАХ)

Как видно из рис. 3, при определенных энергиях происходит спад ВАХ.

Установка:

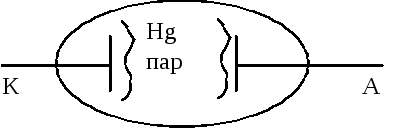
Рис. 4 Экспериментальная установка

Была показана энергетическая дискретность атома ртути, определены энергетические уровни.

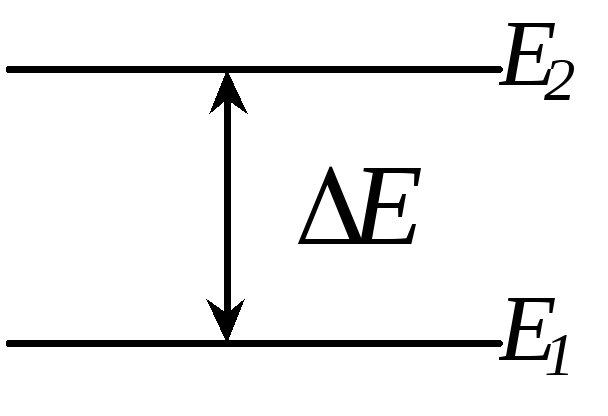
Рис. 5. Энергетические уровни

- порция энергии, которую может отдать атом ртути.

1922. Опыты Штерна и Герлоха по расщеплению атомного пучка в неоднородном магнитном поле.

Рис. 6. Вид магнитов в эксперименте Штерна и Герлоха.

По оси z поле в обкладках магнита неоднородно. Так как есть градиент поля , то если пропускать вдоль осиx частицы, имеющие магнитный момент , то возникает сила:

Наблюдалось расщепление атомного пучка. С точки зрения классической теории все равновероятны и поэтому должна получиться одна широкая полоса. Наблюдались две четкие линии.

Подтвердили, что магнитный момент атома квантуется, т. е. принимает дискретные знвяения.

,

где для серебра.

1923 – 1924 гг. Теория Де Бройля корпускулярно-волнового дуализма частиц. Соотношения теории:





Здесь слева параметры частицы: энергия и импульс. Справа параметры волны: частота, волновой вектор.



Волна Де Бройля

, - длина волны Де Бройля.

1927 г. Дэвиссон-Джермер. Рассеяние электронов на кристаллической решетке. Подтверждение волновых свойст частиц.

§ 2. Классическое и квантовое описание системы.

Опыт № 1. Имеется источник частиц, экран с достаточно узким отверстием. Картину наблюдаем на Э2

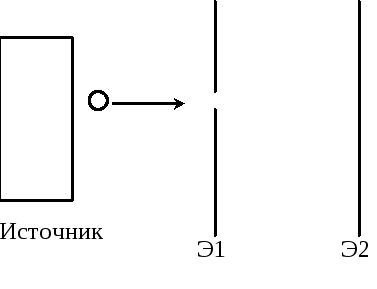
Опыт № 2. Заменяем Э1 на Э1^/.

Опыт № 3. Объединяем экраны Э1 и Э1^/

При классическом описании опыт 3 давал бы сложение интенсивностей от опыта 1 и 2. Однако опыт 3 показал интерференционную картину, а это волновые свойства. Частица с определенной вероятностью проходит как через щель 1 так и через щель 2. Нельзя точно сказать через какую щель пройдет электрон.

Классическая интерпретация (с числом степеней свободы n=1) решается составлением уравнений в форме Гамильтона:

Можно найти траекторию частицы.

В общем случае состояние механической системы определяется 2n динамическими переменными. Т. е. 2n начальных условий.

Но опыт показал, что мы не можем определить траекторию частицы в микромире.

Количество динамических переменных, которые могут быть одновременно измерены в микромире, в квантовой механике – n.

Скорость

Координата

Если известна точка , то чтобы найти положение точкинадо знатьиодновременно, т. е. координаты и импульс должны быть измерены одновременно.

Если мы знаем и, то можем построить траекторию электрона. Однако построить такую траекторию мы не можем (опыт № 3). Тогда мы не можем одновременно измеритьp и q.