
- •Квантовая механика
- •§ 1. Экспериментальные основы квантовой механики
- •§ 2. Классическое и квантовое описание системы.
- •§ 3 Принцип неопределенности.
- •§ 4. Полный набор динамических переменных
- •§ 5. Постулаты квантовой механики.
- •§ 6 Роль классической механики в квантовой механике
- •§ 7 Волновая функция и ее свойства.
- •§ 8 Принцип суперпозиции состояний
- •§ 9 Понятие о теории представлений
- •§ 10 Операторы в квантовой механике
- •§ 12 Среднее значение измеряемой величины.
- •§ 13 Вероятность результатов измерения
- •§ 14 Коммутативность операторов и одновременная измеримость физических величин
- •§ 15. Операторы координаты , импульса, момента импульса, энергии.
- •§ 16. Решение задачи Штурма-Лиувилля для оператора .
- •§ 17 Решение задачи Штурма-Лиувилля для оператора .
- •§ 18. Вычисление коммутаторов, содержащих операторы .
- •§ 19 Волновое уравнение
- •§ 20 Производная оператора по времени
- •§ 21 Интегралы движения в кв. Механике.
- •§ 22. Свойства операторов вида
- •§23. Флуктуации физических величин.
- •§ 24. Неравенство Гайзенберга.
- •§ 25 Оператор Гамильтона различных систем.
- •§ 26. Стационарное состояние различных систем
- •§ 27. Решение волнового уравнения в случае свободной материальной точки
- •Для трехмерного случая
- •§ 28. Интегральные операторы в квантовой механике.
- •§ 29. Интегральный оператор канонического преобразования.
- •§ 30. Каноническое преобразование оператора.
- •§ 31. Уравнения Шредингера в матричной форме.
- •§ 32. Линейный гармонический осциллятор
- •Предельные технологические размеры кристаллов и.С. 0.1 – 0.5 мкм. Существует и предел по физической работоспособности. Однако с уменьшением размера кристалла увеличивается быстродействие приборов.
- •§ 30.1. Каноническое преобразование оператора. Ч. 2
- •§ 34. Унитарные инварианты в квантовой механике.
- •§ 35. Вид операторов ив декартовых и сферических координатах.
- •§ 36. Коммутационные соотношения с оператором .
- •§ 37. Собственные функции и собственные значения операторов и.
- •§ 38. Вырождение энергетических уровней частицы, движущейся в центральном поле.
- •§ 39. Гамильтониан частицы без спина, движущейся в магнитном поле.
- •§ 40. Снятие вырождения по квантовому числу m в случае частицы без спина, движущейся в магнитном поле. Используем
- •§ 41. Оператор бесконечно малого поворота без учета спина.
- •§ 42. Собственный механический момент (спин).
- •§ 43. Операторы ии их свойства.
- •§ 44. Спиновая переменная волновой функции
- •§ 45. Матрицы Паули и их свойства.
- •§ 46 Понятие о спинорах
- •§ 47. Уравнение Паули Мы писали волновое уравнение в виде
- •§ 48. Операторы и, и их свойства
- •§ 50. Принцип тождественности.
- •§ 51. Оператор перестановки и его свойства
- •§ 52. Симметричное и антисимметричное состояния.
- •§ 53. Обменное взаимодействие
- •§ 54. Основное состояние атома гелия
- •§ 55. Схема Юнга квантовой механики.
- •1. И ,
- •2. И .
- •§ 56. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения.
- •§ 58 Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближения.
- •§ 59. Критерий применимости теории возмущений.
- •§ 60. Стационарная теория возмущений в случае близких энергетических уровней.
- •§ 61. Метод (представление) Шредингера. Оператор эволюции и его свойства.
- •§ 62. Метод (представление) Гейзенберга. Уравнение движения для оператора.
- •§ 63. Уравнение эволюции среднего значения физической величины. Соотношение неопределенности: время – энергия.
- •§ 64. Матричное представление операторов.
- •§ 65. E – представление.
- •§ 66. Уравнение Шредингера в матричной форме.
- •§ 67. Матричная формулировка задачи о линейном гармоническом осцилляторе.
- •§ 68. Расчет матричных элементов операторов .
§ 12 Среднее значение измеряемой величины.
По определению
![]() (1)
(1)
Рассмотрим
оператор
![]() с дискретным спектром. Разложим
с дискретным спектром. Разложим![]() по
собственным функциям оператора
по
собственным функциям оператора![]() :
:
![]() (2)
(2)
По
равенству Парсеваля
![]()
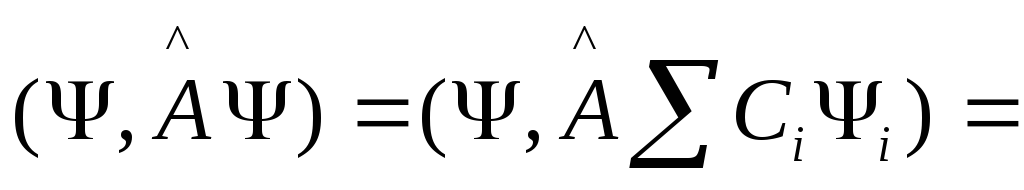 {в
силу линейности оператора заносим его
под знак суммы}
{в
силу линейности оператора заносим его
под знак суммы}
![]() (3)
(3)
Подставляя (3) в числитель, а (2) в знаменатель для (1), тогда имеем
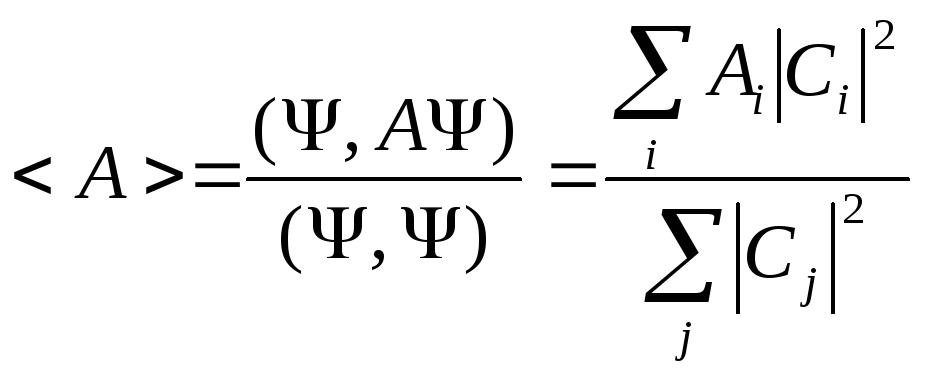 (4)
(4)
Из
теории вероятности
![]() ,
где
,
где![]() - вероятность получения
- вероятность получения![]() ,
тогда
,
тогда

§ 13 Вероятность результатов измерения
![]() - вероятность того, что при измерении
величины
- вероятность того, что при измерении
величины![]() для системы, находящейся в состоянии
для системы, находящейся в состоянии![]() мы получим результат
мы получим результат![]() .
.
Если
система находится в состоянии
![]() ,
то величина
,
то величина![]() при измерении выходит с вероятностью
равной 1:
при измерении выходит с вероятностью
равной 1:
![]()
В
общем случае
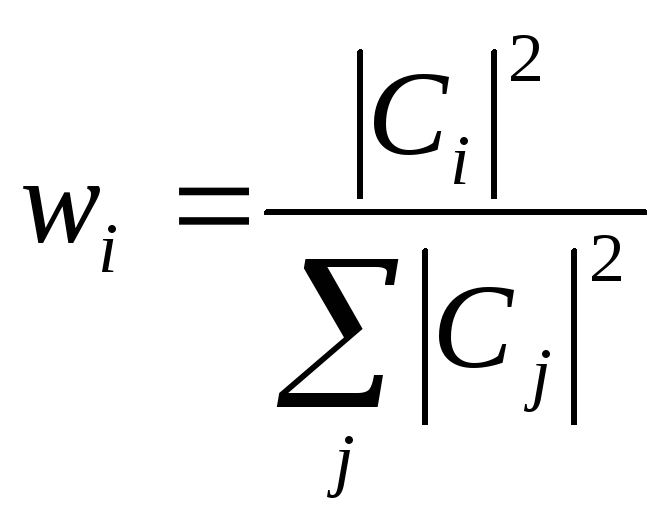 .
.
Условие
при котором собственная функция оператора
![]() описывает состояние системы:
описывает состояние системы:
Если
полная производная оператора
![]() удовлетворяет
равенству
удовлетворяет
равенству
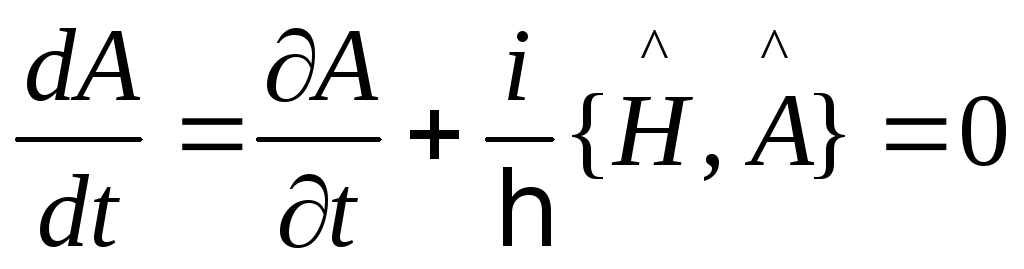
Для
непрерывного спектра, вероятность того,
что результаты измерения величины A
для системы, находящейся в состоянии
![]() ,
лежат в интервале
,
лежат в интервале ![]() ,
определяется следующим значением:
,
определяется следующим значением:

или
плотность вероятности
![]()
§ 14 Коммутативность операторов и одновременная измеримость физических величин
Введем понятие коммутатора
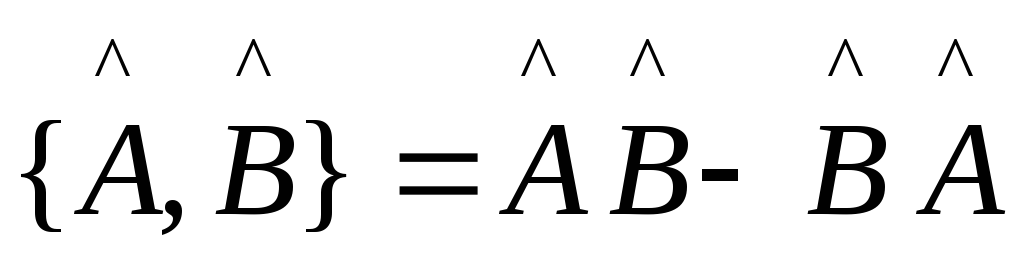
Если
мы имеем
![]() ,
то предполагается, что на некоторую
функцию
,
то предполагается, что на некоторую
функцию![]() сначала действует
сначала действует![]() ,
а потом на все действует
,
а потом на все действует![]() .
.
Если
![]() ,
то операторы
,
то операторы![]() и
и![]() коммутативны. Причем физические величины,
соответствующие этим операторам
одновременно измеримы. Или говорят, что
эти операторы имеют общий базис. То есть
все собственные функции этих операторов
можно выбрать общими.
коммутативны. Причем физические величины,
соответствующие этим операторам
одновременно измеримы. Или говорят, что
эти операторы имеют общий базис. То есть
все собственные функции этих операторов
можно выбрать общими.
Разложим
![]() по базису:
по базису:
![]() .
.
Подействуем
на
![]() коммутатором:
коммутатором:
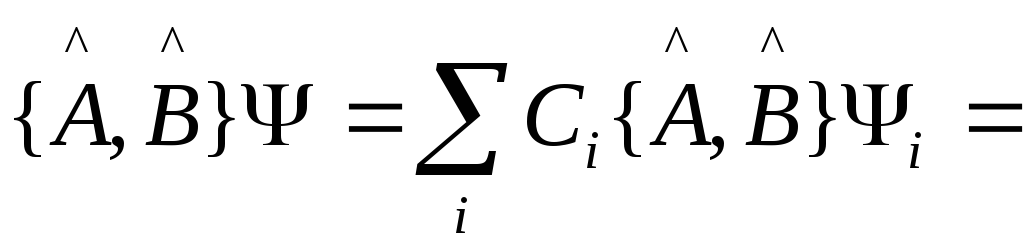 {Используем
то, что
{Используем
то, что
![]() образуют общий базис. }=
образуют общий базис. }=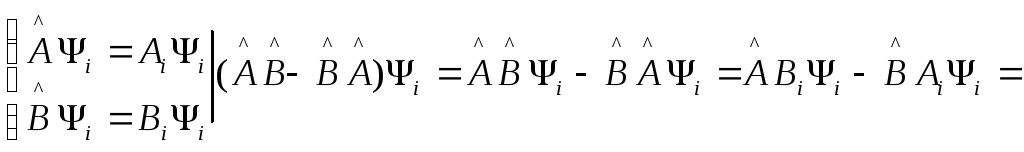 {Числа
с оператором коммутируют (т. к. операторы
эрмитовы)}
=
{Числа
с оператором коммутируют (т. к. операторы
эрмитовы)}
=
![]()
То есть, если физические величины одновременно измеримые, то их коммутатор равен нулю.
Обратное:
Если коммутатор обращается в ноль, то физические величины одновременно измеримы.
Пусть
![]() собственная функция задачи Штурма-Лиувилля
собственная функция задачи Штурма-Лиувилля
 .
Подставляем ее в коммутатор
.
Подставляем ее в коммутатор

Тогда
получим 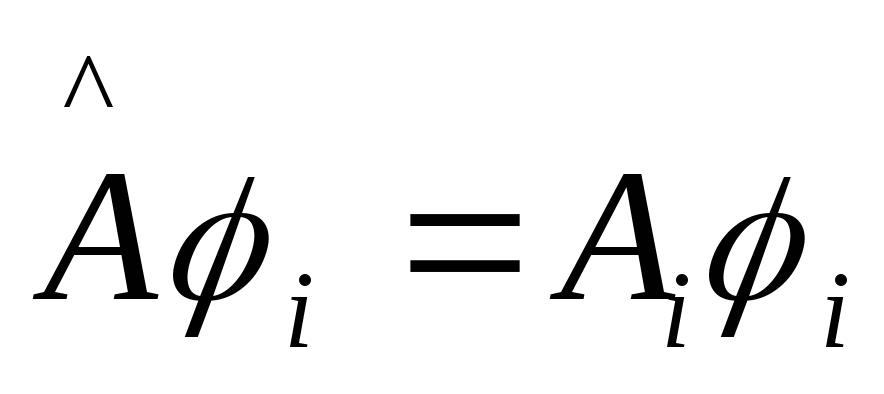 .
Мы рассматриваем невырожденный спектр.
Это значит, что существует однозначное
соответствие одно собственного значения
и одной собственной функции. Разница
между функциями
.
Мы рассматриваем невырожденный спектр.
Это значит, что существует однозначное
соответствие одно собственного значения
и одной собственной функции. Разница
между функциями ![]() и
и ![]() только до константы.
только до константы.
Пусть
эта константа ![]() ,
тогда
,
тогда ![]() .
Но
.
Но  ,
тогда
,
тогда 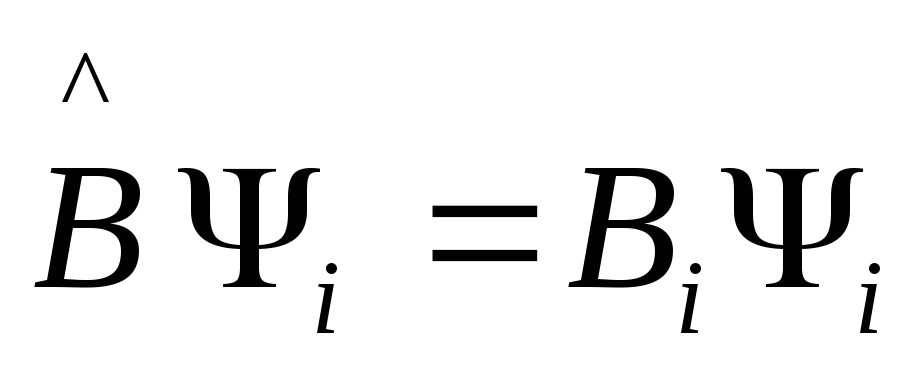 .
.
Мы
получили, что функция
![]() удовлетворяет задаче Штурма-Лиувилля
для оператора
удовлетворяет задаче Штурма-Лиувилля
для оператора![]() .
.
Это
можно было показать для любой собственной
функции оператора
![]() .
.
Тогда
из коммутативности операторов
![]() и
и![]() следует общность базисов.
следует общность базисов.
Величины
![]() и
и![]() ,
которым соответствуют коммутирующие
операторы могут быть одновременно
измеримы и следовательно могут
образовывать полный набор динамических
переменных.
,
которым соответствуют коммутирующие
операторы могут быть одновременно
измеримы и следовательно могут
образовывать полный набор динамических
переменных.
Полный
набор динамических переменных полностью
задает состояние системы. Но операторы
![]() и
и![]() должны
быть независимы.
должны
быть независимы.
§ 15. Операторы координаты , импульса, момента импульса, энергии.
Будем
использовать координатное представление
(![]() -представление).
Будем рассматривать систему из одной
материальной точки.
-представление).
Будем рассматривать систему из одной
материальной точки.
Действие
![]() сводится
к умножению
на вектор
сводится
к умножению
на вектор
![]() ,
т. е.
,
т. е.
![]() (это определение действия оператора,
но не задача Штурма-Лиувилля).
(это определение действия оператора,
но не задача Штурма-Лиувилля).
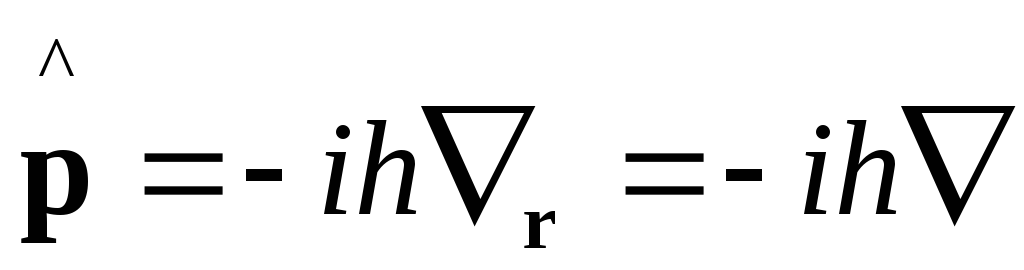
![]()
Здесь строго соблюдается последовательность операторов при раскрытии векторного произведения, например, первая компонента:
![]() ,
,
однако для частного случая декартовых координат порядок операторов не существенен.
Оператор
энергии или Гамильтониан
![]() .
.
![]() ,
,
здесь
![]() -
оператор кинетической энергии,
-
оператор кинетической энергии,![]() - оператор потенциальной энергии.
- оператор потенциальной энергии.
Для одной материальной точки гамильтониан имеет вид:
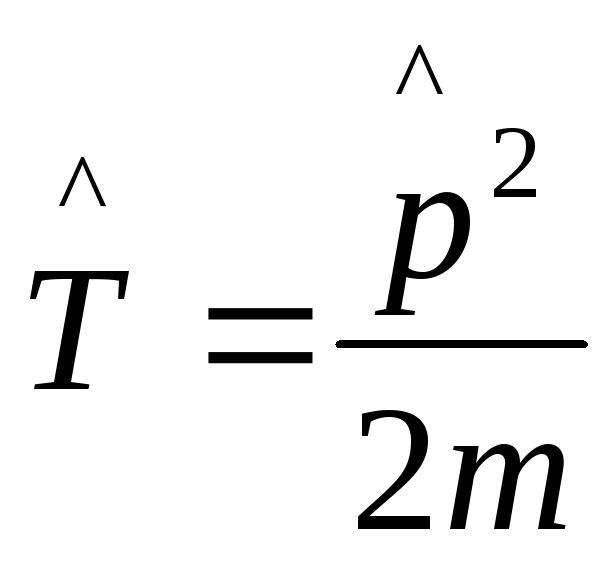
![]()
Координата t – признак внешнего нестационарного поля.
Для
одной материальной точки:
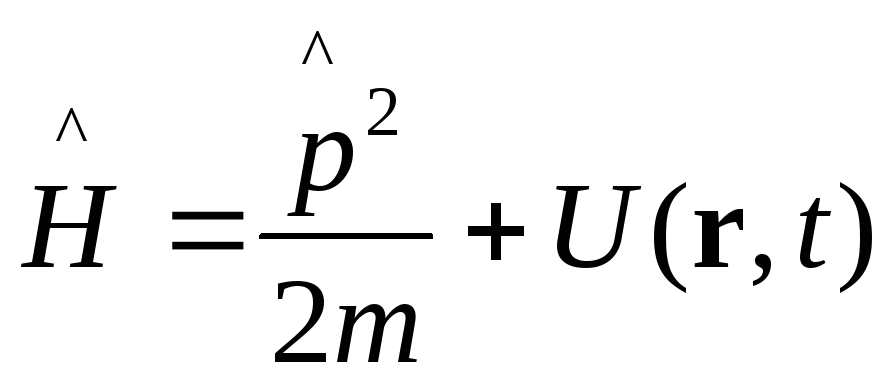 .
Тут присутствует
.
Тут присутствует
![]() и
и![]() ,
но
,
но![]() и
и![]() одновременно не измеримы, тогда
потенциальная и кинетическая энергия
в квантовой механике не могут быть
одновременно измерены. В квантовой
механике существует понятие “энергия
частицы”, но порознь вводить энергию
нельзя, иначе либо
одновременно не измеримы, тогда
потенциальная и кинетическая энергия
в квантовой механике не могут быть
одновременно измерены. В квантовой
механике существует понятие “энергия
частицы”, но порознь вводить энергию
нельзя, иначе либо![]() ,
либо
,
либо![]() оказываются
неизвестными.
оказываются
неизвестными.
