
- •Квантовая механика
- •§ 1. Экспериментальные основы квантовой механики
- •§ 2. Классическое и квантовое описание системы.
- •§ 3 Принцип неопределенности.
- •§ 4. Полный набор динамических переменных
- •§ 5. Постулаты квантовой механики.
- •§ 6 Роль классической механики в квантовой механике
- •§ 7 Волновая функция и ее свойства.
- •§ 8 Принцип суперпозиции состояний
- •§ 9 Понятие о теории представлений
- •§ 10 Операторы в квантовой механике
- •§ 12 Среднее значение измеряемой величины.
- •§ 13 Вероятность результатов измерения
- •§ 14 Коммутативность операторов и одновременная измеримость физических величин
- •§ 15. Операторы координаты , импульса, момента импульса, энергии.
- •§ 16. Решение задачи Штурма-Лиувилля для оператора .
- •§ 17 Решение задачи Штурма-Лиувилля для оператора .
- •§ 18. Вычисление коммутаторов, содержащих операторы .
- •§ 19 Волновое уравнение
- •§ 20 Производная оператора по времени
- •§ 21 Интегралы движения в кв. Механике.
- •§ 22. Свойства операторов вида
- •§23. Флуктуации физических величин.
- •§ 24. Неравенство Гайзенберга.
- •§ 25 Оператор Гамильтона различных систем.
- •§ 26. Стационарное состояние различных систем
- •§ 27. Решение волнового уравнения в случае свободной материальной точки
- •Для трехмерного случая
- •§ 28. Интегральные операторы в квантовой механике.
- •§ 29. Интегральный оператор канонического преобразования.
- •§ 30. Каноническое преобразование оператора.
- •§ 31. Уравнения Шредингера в матричной форме.
- •§ 32. Линейный гармонический осциллятор
- •Предельные технологические размеры кристаллов и.С. 0.1 – 0.5 мкм. Существует и предел по физической работоспособности. Однако с уменьшением размера кристалла увеличивается быстродействие приборов.
- •§ 30.1. Каноническое преобразование оператора. Ч. 2
- •§ 34. Унитарные инварианты в квантовой механике.
- •§ 35. Вид операторов ив декартовых и сферических координатах.
- •§ 36. Коммутационные соотношения с оператором .
- •§ 37. Собственные функции и собственные значения операторов и.
- •§ 38. Вырождение энергетических уровней частицы, движущейся в центральном поле.
- •§ 39. Гамильтониан частицы без спина, движущейся в магнитном поле.
- •§ 40. Снятие вырождения по квантовому числу m в случае частицы без спина, движущейся в магнитном поле. Используем
- •§ 41. Оператор бесконечно малого поворота без учета спина.
- •§ 42. Собственный механический момент (спин).
- •§ 43. Операторы ии их свойства.
- •§ 44. Спиновая переменная волновой функции
- •§ 45. Матрицы Паули и их свойства.
- •§ 46 Понятие о спинорах
- •§ 47. Уравнение Паули Мы писали волновое уравнение в виде
- •§ 48. Операторы и, и их свойства
- •§ 50. Принцип тождественности.
- •§ 51. Оператор перестановки и его свойства
- •§ 52. Симметричное и антисимметричное состояния.
- •§ 53. Обменное взаимодействие
- •§ 54. Основное состояние атома гелия
- •§ 55. Схема Юнга квантовой механики.
- •1. И ,
- •2. И .
- •§ 56. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения.
- •§ 58 Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближения.
- •§ 59. Критерий применимости теории возмущений.
- •§ 60. Стационарная теория возмущений в случае близких энергетических уровней.
- •§ 61. Метод (представление) Шредингера. Оператор эволюции и его свойства.
- •§ 62. Метод (представление) Гейзенберга. Уравнение движения для оператора.
- •§ 63. Уравнение эволюции среднего значения физической величины. Соотношение неопределенности: время – энергия.
- •§ 64. Матричное представление операторов.
- •§ 65. E – представление.
- •§ 66. Уравнение Шредингера в матричной форме.
- •§ 67. Матричная формулировка задачи о линейном гармоническом осцилляторе.
- •§ 68. Расчет матричных элементов операторов .
§ 6 Роль классической механики в квантовой механике
Два момента присутствия классической механики в квантовой механике
Измерение микросистем (квантово-механических систем) проводятся с помощью классических приборов (систем)
Принцип соответствия – переход квантово-механических результатов в классическую механику ( 0. Можно ввести такую величину размерности действия A, что
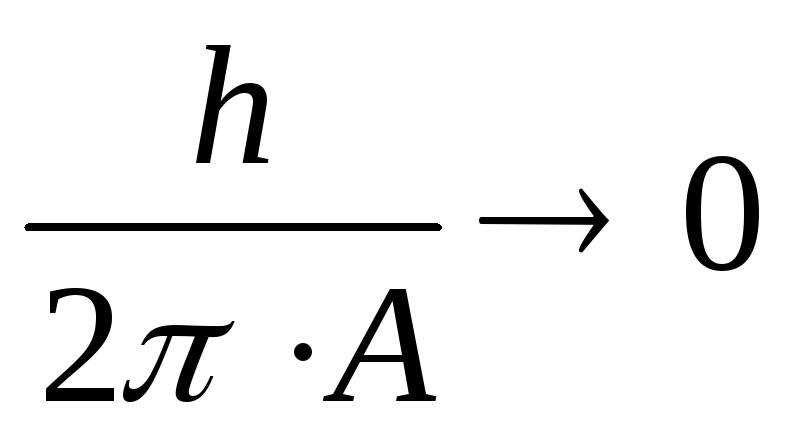 ).
).
По
Эйнштейну этот переход характеризуется
![]() .
Если
.
Если![]() ,
то переход в классическую механику
Ньютона.
,
то переход в классическую механику
Ньютона.
§ 7 Волновая функция и ее свойства.
Волновая функция динамических переменных и времени определяет состояние системы точностью до фазового множителя. Т. е.
![]()
т.
е.
![]() ,
,![]() описывает
одно и тоже состояние, где
описывает
одно и тоже состояние, где![]() - фазовый множитель.
- фазовый множитель.
Волновая функция – комплексная, непрерывная, конечная. У нее почти всюду существует конечная производная по координате, но в некоторых точках может терпеть скачек (особые точки).
Функции
![]() -
нормируемые, т.е. квадратично интегрируемы.
Но для свободной материальной точки
-
нормируемые, т.е. квадратично интегрируемы.
Но для свободной материальной точки![]() не
нормируема.
не
нормируема.
![]()
![]() -
элементарный объем
-
элементарный объем
![]() -
вероятность того, что динамические
переменные
-
вероятность того, что динамические
переменные
![]() лежат в интервале
лежат в интервале![]() .
.
Это определение справедливо для квадратично интегрируемых функций.
Для
не квадратично интегрируемых функций
величина
![]() пропорциональна плотности вероятности.
пропорциональна плотности вероятности.
§ 8 Принцип суперпозиции состояний
Если
мы имеем состояние системы, описываемое
функцией
![]() ,
то суперпозиции этих функций отвечает
некоторое состояние этой системы
,
то суперпозиции этих функций отвечает
некоторое состояние этой системы
![]()
Иначе:
если
![]() -
состояние некоторой системы, то
суперпозиция этих состояний также
является состоянием этой системы.
-
состояние некоторой системы, то
суперпозиция этих состояний также
является состоянием этой системы.
Отсюда
получаем: уравнения, которым подчиняется
![]() -
функция должны быть линейными.
-
функция должны быть линейными.
Этот же вывод распространяется и на операторы и на операторы в квантовой механике. Принцип суперпозиции требует использования в квантовой механике линейных операторов.
§ 9 Понятие о теории представлений
Представление – это совокупность переменных в которых решается задача (т. е. набор динамических переменных).
Рассмотрим одну материальную точку. Число степеней свободы n=3.
Здесь могут быть 2 случая:
Под
 понимаем
понимаем
 имеем
имеем -представление
(координатное)
-представление
(координатное)Под
 понимаем
понимаем
 имеем
имеем -представление
(импульсное)
-представление
(импульсное)
Операторы
в
![]() -представлении:
-представлении:
Оператор
координаты
![]()
Оператор
импульса
![]()
![]()
Здесь
![]()
Операторы
в
![]() -представлении
-представлении
Оператор
координаты
![]()
![]()
Оператор
импульса
![]()
Здесь
![]()
Мы
в основном будем использовать
![]() -представление.
-представление.
Результаты измерения от вида представления не зависят!
§ 10 Операторы в квантовой механике
В силу принципа суперпозиции в квантовой механике используются линейные операторы.
Линейный
оператор – это такой оператор
![]() действующий на
действующий на![]() ,
что
,
что
 (1)
(1)
![]() (2)
(2)
здесь
– задача Штурма-Лиувилля
-
 действует на произвольную функцию
действует на произвольную функцию .
.
Линейность:
Если
![]() ,
то
,
то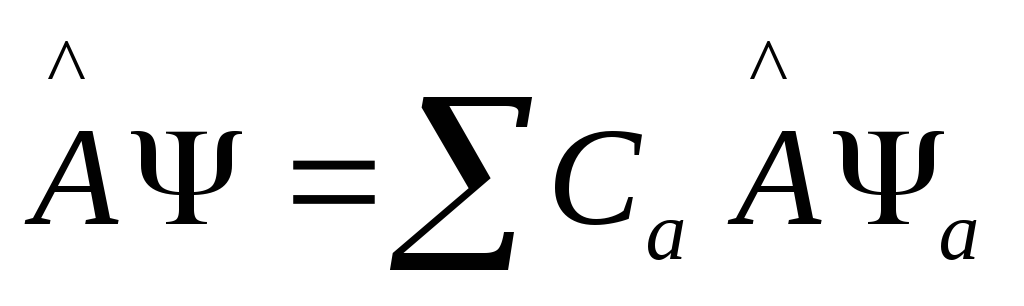 (3)
(3)
т.к.
![]() ,
то из (3)
,
то из (3)![]()
Сопряженный оператор – это оператор, который связан с данным оператором соотношением:

или

Отсюда

Если
![]() -
то оператор называется эрмитовым.
-
то оператор называется эрмитовым.
Транспонированный оператор
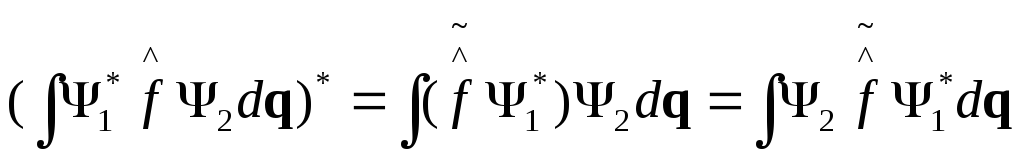
Отметим следующие свойства:
1)
![]()
 (4)
(4)
Из выражения (4) получаем
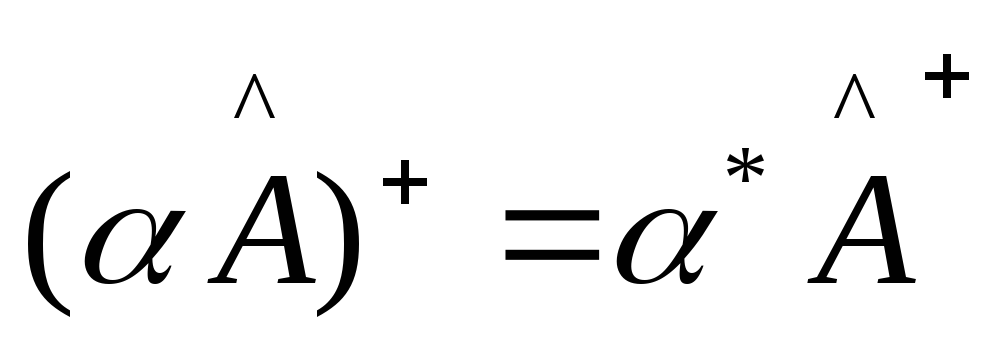
2)
![]()
3)

Сумма
операторов:
![]() . Это операторное равенство предполагает
. Это операторное равенство предполагает
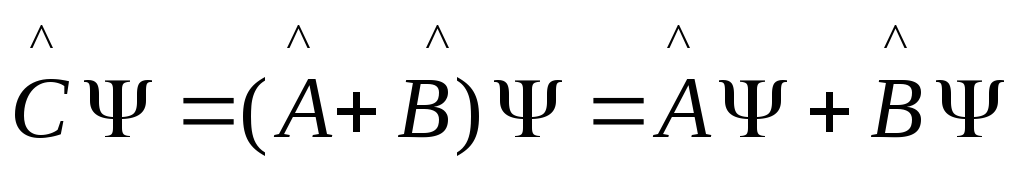
Произведение
операторов:
![]() ,
тогда
,
тогда
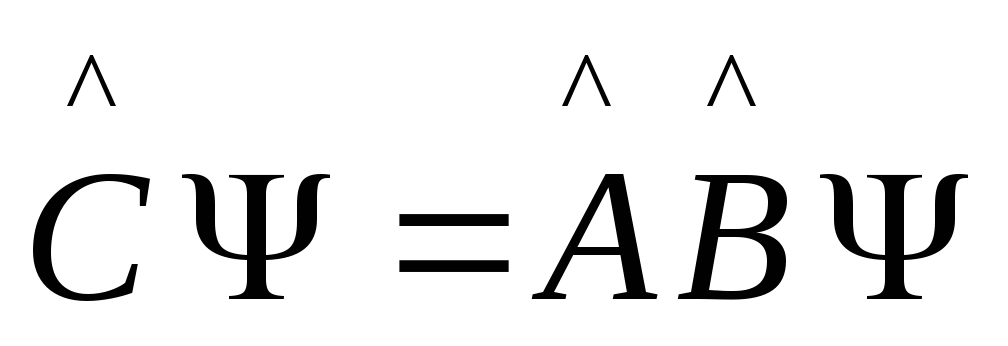 .
Это операторное равенство предполагает
.
Это операторное равенство предполагает
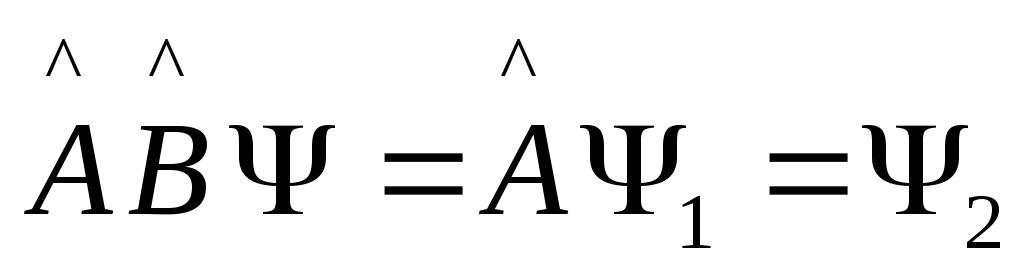
В
общем случае
![]() не коммутативны
не коммутативны
![]()
Коммутатор
![]()
Если ![]() ,
то операторы коммутативны.
,
то операторы коммутативны.
Если
![]() ,
то операторы не коммутативны.
,
то операторы не коммутативны.
Так как физические величины вещественны, то число операторов в квантовой механике сужается.
Сужение класса операторов – эрмитовость операторов.
Запишем определение среднего:

Так
как результаты измерений вещественны,
то
![]() тоже должно быть вещественным, т.е.
тоже должно быть вещественным, т.е.
![]() (5)
(5)
тогда
![]() ,
,
т.е.
![]()
Обозначим
![]() ,
тогда
,
тогда
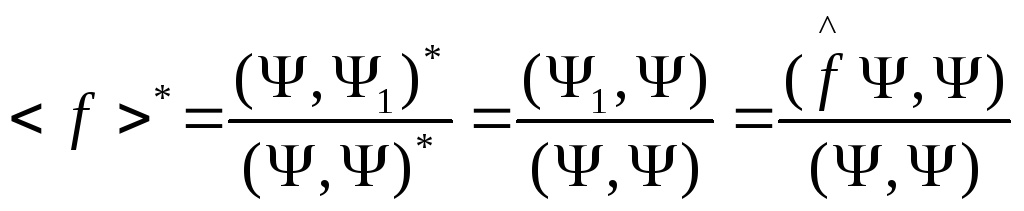
Тогда из (5) получаем
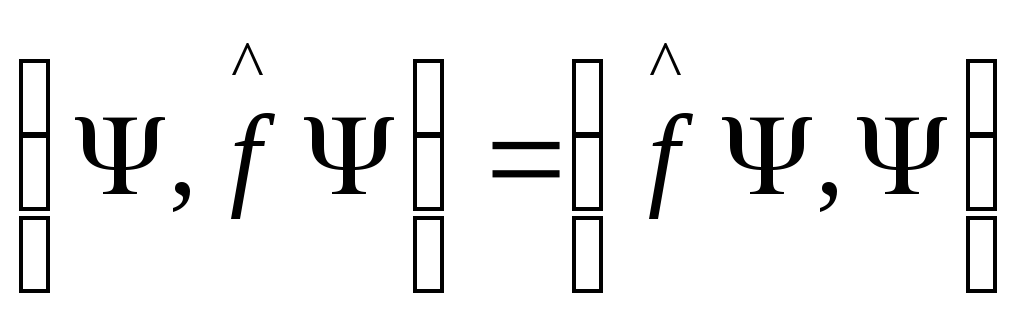 (6)
(6)
Из
(6) имеем для любых
![]() :
:
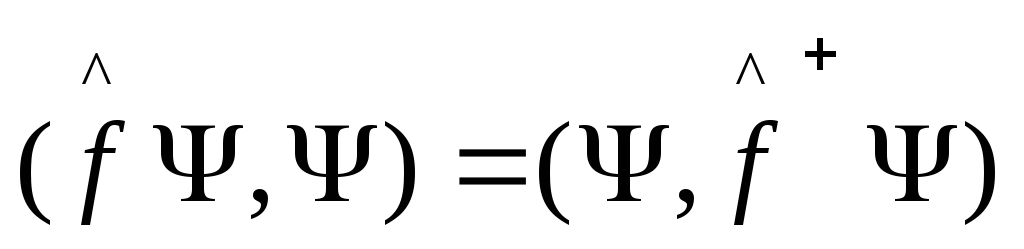 ,
,
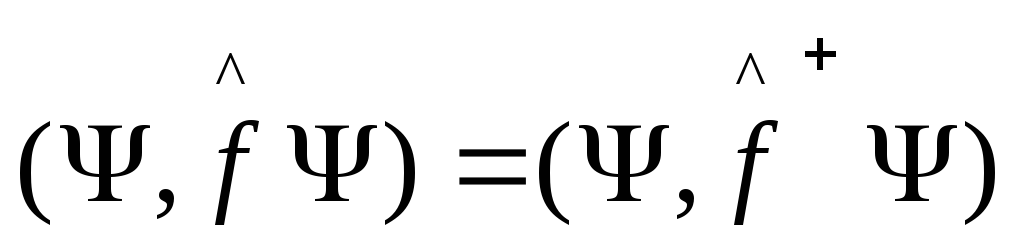 ,
,
![]()
где
 (сопряженный
и транспонированный)
(сопряженный
и транспонированный)
§ 11. Собственные функции и собственные значения эрмитовых операторов. Случаи дискретного и непрерывного спектров.
Начнем с дискретного спектра, т.к. ему соответствует квадратичноинтегрируемые функции.
Задача Штурма-Лиувилля дискретного спектра
 (1)
(1)
![]() -собственные
функции
-собственные
функции
![]() - собственные значения
- собственные значения
Так
как
![]() эрмитов, то его собственные значения
вещественны.
эрмитов, то его собственные значения
вещественны.
Расчет
среднего
 .
Если речь идет о физической величине,
то
.
Если речь идет о физической величине,
то![]() это
волновые функции (описывающие состояние
системы). Если речь идет о математическом
аппарате, то
это
волновые функции (описывающие состояние
системы). Если речь идет о математическом
аппарате, то![]() -
это любые функции.
-
это любые функции.
Как
частные случай рассмотрим
![]() ,
где
,
где![]() - собственные функции оператора
- собственные функции оператора![]() .
Тогда
.
Тогда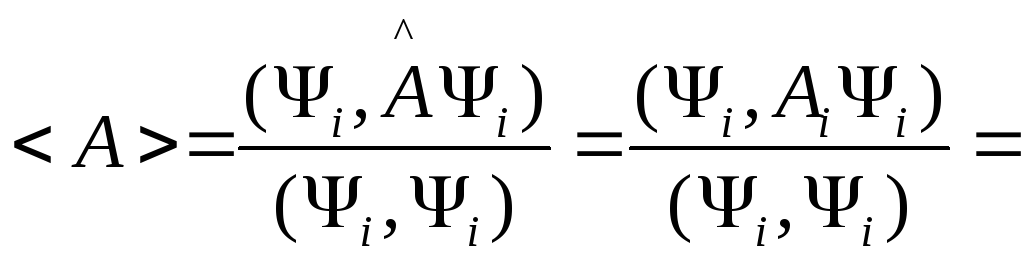 {Так
как
{Так
как![]() - число, то его можно вынести за знак
скалярного произведения}
- число, то его можно вынести за знак
скалярного произведения} - это среднее значение величины
- это среднее значение величины![]() вi-ом
квантовом состоянии.
вi-ом
квантовом состоянии.
Так как среднее – вещественно, то и собственные значения вещественны.
Для
эрмитова оператора
![]() собственные значения вещественны
собственные значения вещественны![]() .
Все эрмитовы операторы имеют вещественные
спектры.
.
Все эрмитовы операторы имеют вещественные
спектры.
Рассмотрим
теперь
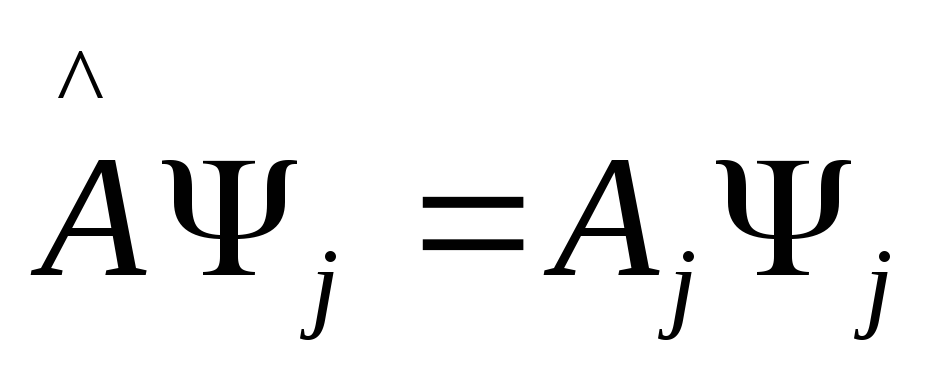
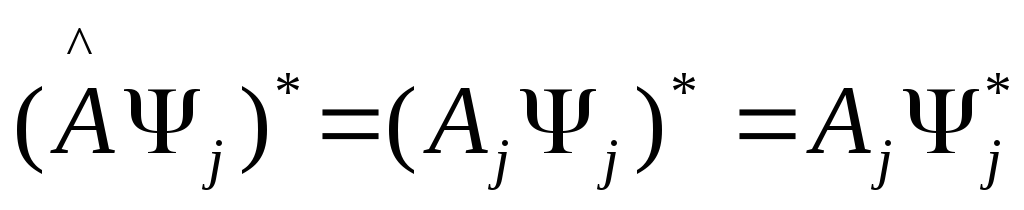 (2)
(2)
Умножая
(1) скалярно на
![]() слева, получим
слева, получим
 (3)
(3)
Теперь
(2) умножаем справа на
![]() ,
тогда
,
тогда
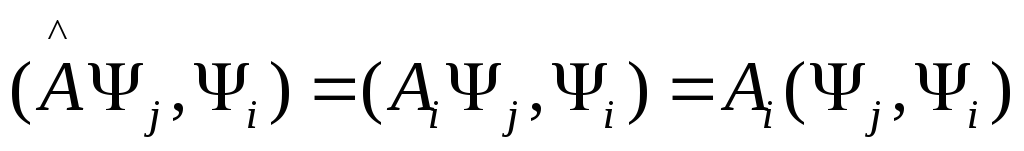 (4)
(4)
Почленно из (3) – (4):
 (5)
(5)
т.к.
![]() - эрмитов, то
- эрмитов, то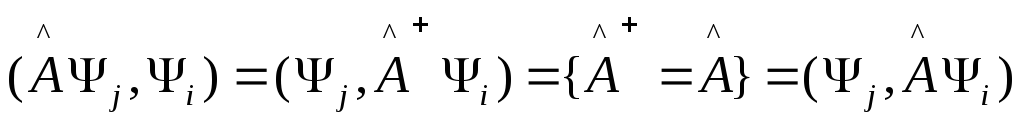 .
Из (5) имеем
.
Из (5) имеем
![]() . (6)
. (6)
Рассмотрим случай невырожденного спектра:
Спектр вырожденный, если одному собственному значению
соответствуют несколько собственных функций.
Например:
![]()
Невырожденный спектр – все собственные значения различные.
1)
Рассмотрим (6) при
![]() ,
тогда
,
тогда![]() ,
,![]() .
.
2)
Теперь пусть
![]() .
В этом случае скалярное произведение
.
В этом случае скалярное произведение![]() .
Обычно вводят нормировку
.
Обычно вводят нормировку![]() .
.
1
и 2 дает условие ортонормируемости
![]() .
.
Утверждается, что собственные функции эрмитового оператора с дискретным спектром образуют полную систему, т.е. обладают свойством полноты. Это верно для функций квантовой механики. Утверждение означает, что произвольную функцию можно разложить по собственным функция эрмитовова оператора как по базису.
Запишем это разложение:
![]() ,
(9)
,
(9)
где индекс i пробегает по всем значениям, удовлетворяющим задаче (1).
Формулу (9) следует отличать от принципа суперпозиции
![]() ,
,
где
![]() -
вес состояния
-
вес состояния![]() и суммирование ведется по произвольнымa=1,…,k.
Заметим, что если
и суммирование ведется по произвольнымa=1,…,k.
Заметим, что если
![]() (модель Юнга с ширмой и электроном), то
(модель Юнга с ширмой и электроном), то![]() .
.
Найдем
коэффициенты
![]() из (9). Домножим скалярно (9) на
из (9). Домножим скалярно (9) на![]() ,
тогда имеем
,
тогда имеем![]() {из
условия ортонормированности
{из
условия ортонормированности![]() }=
}=![]()
![]() ,
,
тогда из (9) получаем
![]() ,
,
![]() (9/)
(9/)
Далее
![]()
Из (9/) также можно получить еще одно соотношение:
![]() -
равенство Парсеваля (условие замкнутости).
-
равенство Парсеваля (условие замкнутости).
Теперь рассмотрим случай непрерывного спектра.
 -
у собственной функции индексом является
собственное значение. Собственные
значения непрерывны, они сплошь заполняют
соответствующую числовую ось.
-
у собственной функции индексом является
собственное значение. Собственные
значения непрерывны, они сплошь заполняют
соответствующую числовую ось.
В этом случае собственные функции не нормируемы (квадратично не интегрируемы).
Используем искусственную операцию – введем понятие собственных дифференциалов, по определению:
![]() ,
,
т.
е. на числовой оси рассмотрим функции
с равным весом на интервале
![]() .
.
Собственные дифференциалы (12) квадратичноинтегрируемы. Через рассмотренные собственные дифференциалы приходим к рассмотрению собственных функций.
Условие
ортонормируемости:
![]() .
.
Здесь
уже
![]() дает расходящийся интеграл, т. е. равен
дает расходящийся интеграл, т. е. равен![]() .
.
Собственные
функции
![]() обладают свойством полноты, т. е. они
образуют базис по которому может быть
разложена любая функция:
обладают свойством полноты, т. е. они
образуют базис по которому может быть
разложена любая функция:
![]() ,
,
![]() (13)
(13)
По аналогии с дискретным спектром:
![]()
![]() -
равенство Парсеваля
-
равенство Парсеваля
